POM模式在渤海油气开发环境条件计算中的应用＊

杨圣和 兰志刚 何 琦 张 杰 石新刚

（中海油能源发展股份有限公司北京分公司）

随着海流数值模式逐步发展与完善，特别是其时空覆盖和分辨能力的加强，利用海流数值模式可以从整体上研究更大时空尺度的海洋环流现象，同时也为海洋工程设计参数的计算提供了更多的技术手段［1－2］。由于海洋测量的复杂性，多数海区海流调查资料稀缺或观测序列短，无法单纯利用观测资料完成海洋工程所需要的设计条件、一般作业条件以及疲劳条件的统计分析。通过海流数值模拟计算，不仅可以实现多源数据的融合和同化，同时可以根据需要在三维空间尺度上给出长时间序列的海流模拟结果，从而使重现期极值分析成为可能。本文利用实测数据验证了普林斯顿海流模式（POM）在渤海的适用性，并利用模拟结果计算了渤海不同海区的海流设计条件。

1 方法原理简介

目前国内外的海流数值模式基本上是以三维原始方程为基础［3－4］，水平网格选取多为 Arakawa B或C网格，垂向分层则有深度z坐标、随地σ坐标、等密面ρ坐标和s坐标（伸展坐标）等（有的模式则采用混合坐标，即在不同的层面上根据不同的层化结构分别采用不同的坐标），大部分模式的差分格式多采取有限差分（有限体积）格式，少数采用有限元格式或谱离散模式。其中，Prinston大学的POM海流模式对于不同的垂向分层坐标方案随地σ坐标的模式编程相对简单，能较准确地模拟地形效应，特别是垂向混合系数由二阶湍流闭合模型确定，在一定程度上摆脱了人为因素的干扰［5］，因此在海洋研究和工程计算中均得到了很好的实际应用。

描述海洋中水动力和热力系统的基本控制方程包括：海水运动的动量方程、质量守恒的连续方程、海水的状态方程、温度和盐度的守恒方程等，表现形式如下［6］：

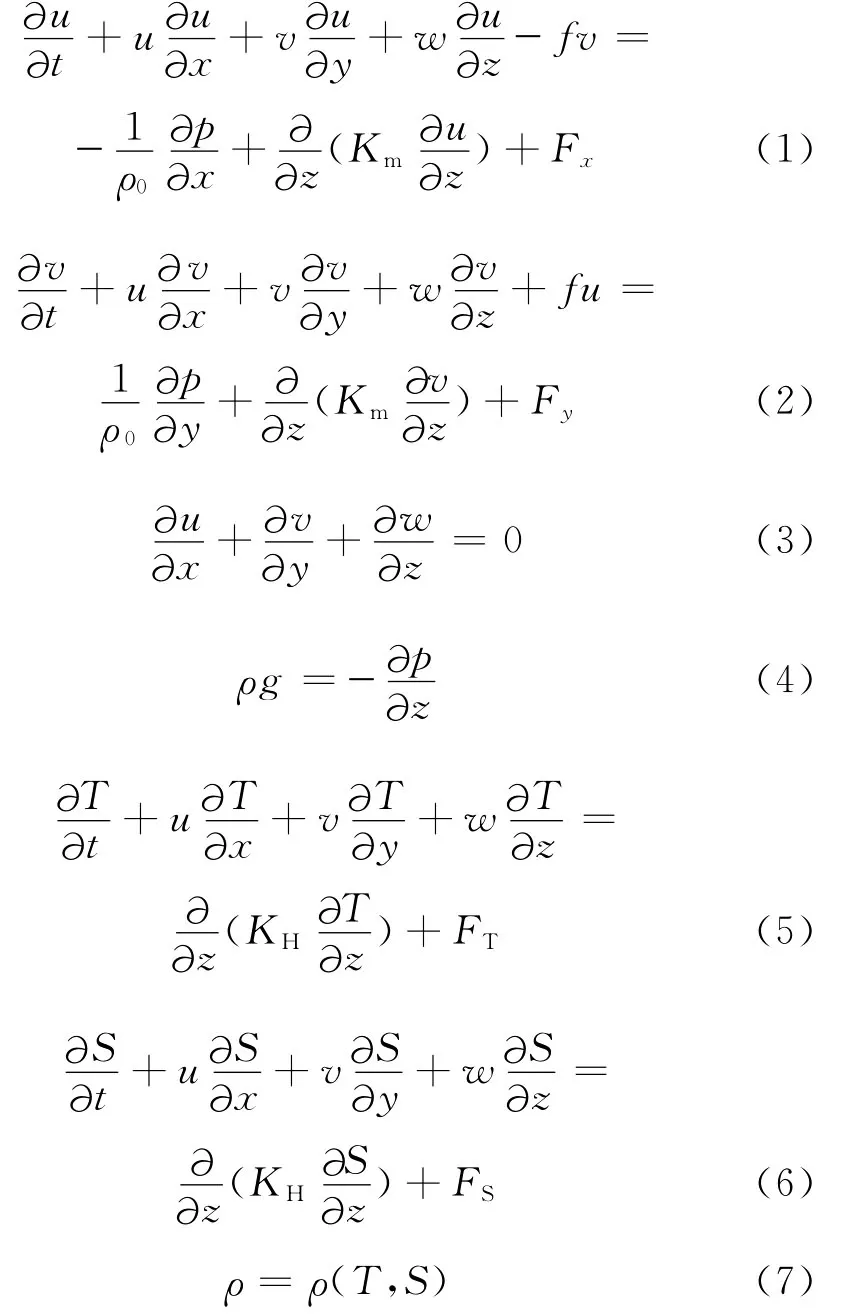
式（1）～（7）中：x、y、z分别为笛卡儿坐标系中的东、北和垂直方向；u、v和w分别为x、y、z方向的流速分量；T为温度；S为盐度；ρ为密度；p为压力；f为科里奥利参数；g为重力加速度；Km为垂向湍粘性系数；KH为热力学垂向湍扩散系数；Fx、Fy、FT、FS分别为水平动量以及温度和盐度的扩散项。

2 边界条件及参数设置

利用POM模式开展渤海油气开发环境条件模拟计算时，海面水位的开边界条件由边界处主要分潮的调和常数通过计算得到［7－9］；流速的开边界条件采用辐射条件或无梯度边界条件给定；温度和盐度的开边界条件采用无梯度边界条件或者出流区辐射、入流区迎风对流格式；将历史观测资料得到的多年平均温度和盐度场作为模式的初始场；POM模式的上表面强迫采用风应力强迫［10］，所用的风应力数据根据大气数值预报模式RAMS输出的风场通过经验公式计算确定；POM模式的开边界采用潮汐的调和常数进行强迫，所用的潮汐调和常数来自于渤海、黄海、东海潮汐模式模拟结果［9］，采用与参考文献［9］中相同数值模拟区域，分辨率为127 mm。POM模式运行和参数设置如下：计算的海区为32～41°N、117.42～126.25°E所覆盖的渤海区域（图1），水平分辨率为127 mm×127 mm，模式采用随地σ坐标，垂向分21层，并且上表层具有较高的分辨率；外模的时间步长为20 s，内模的时间步长为1200 s，积分时间从1985年1月1日至2004年12月31日；流场、水位都采用零初始条件；考虑 M2、S2、O1、K1四个分潮作用，并通过水位调和常数从开边界引入，将风应力均匀差值到模式运行的每一步；每小时输出一次计算结果，包含表层、中层、底层3层流速和水位。

图1 渤海POM模式计算区域及地形分布（图中数字为水深）

3 模拟结果对比检验

3.1 调和常数检验

利用上述的POM模式配置，对渤海的M2、S2、O1、K1分潮进行数值模拟。表1为POM模式模拟的M2分潮调和常数与环渤海各验潮站观测的调和常数对比，可以看出，19个验潮站观测值和模拟的调和常数平均振幅误差只有4.5 cm，平均位相误差只有4.2°，计算稳定后所得到的调和常数与观测结果符合较好。分析认为，二者之间的差异，一方面可能是由于网格点与验潮站之间的位置差异所造成，因为模式的水平网格距都在数千米间，这样的网格对于海岸线的分辨率仍然是比较差的；另一方面可能是由于岸界变迁以及地形和水深的误差所致，这在黄河口和莱州湾表现得尤其明显；另外还有可能与边界处各分潮的调和常数精度等条件有关。

表1 用POM模式模拟的M2分潮调和常数与环渤海验潮站观测的调和常数的对比

3.2 海流检验

选取共计8个有代表性的天气过程，利用渤海QK 18－1、SZ 36－1、JZ 20－2、JZ 9－3和 LD 16－3 共5个海洋石油开发区的现场潮流实测资料对模拟结果进行对比检验。根据公式σ＝Δ/L×100%（其中σ为流速、流向相对误差；Δ为流速、流向模拟与实测差值；L为流速、流向实测值），对模拟结果和实测资料作对比分析，结果见表2。

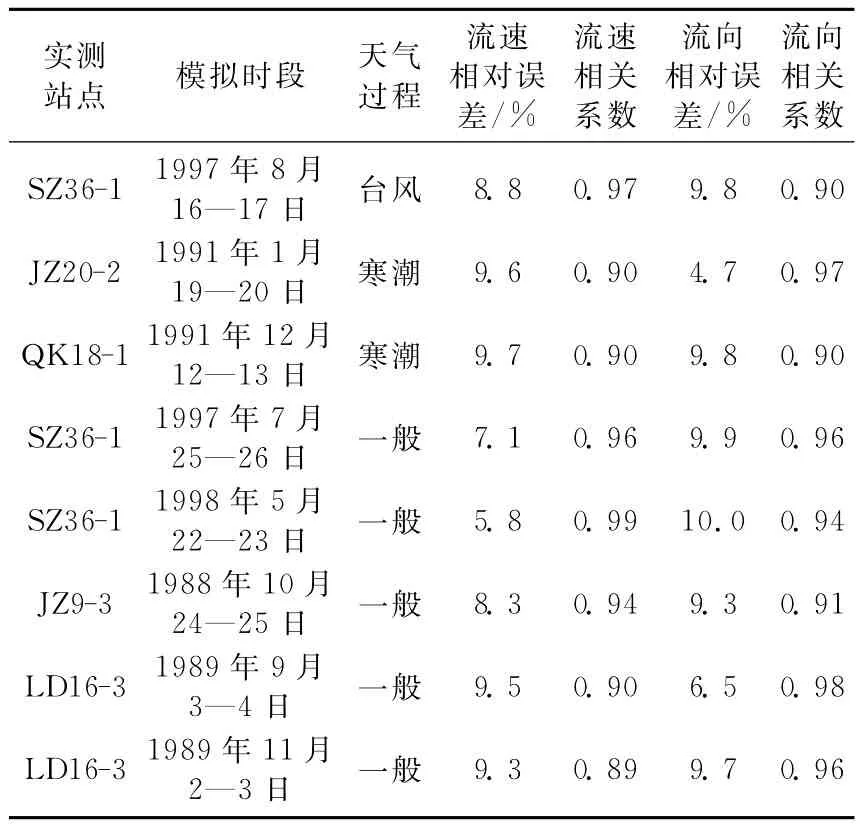
表2 现场实测和模拟计算的渤海海流流速和流向对比

从表2可以看出，流速模拟计算结果和现场实测值相对误差为5.8%～9.7%，二者之间的相关系数为0.89～0.99；流向模拟计算结果和现场实测值相对误差为4.7%～10.0%，二者之间的相关系数为0.90～0.98。这说明，模拟的潮流和实际观测的潮流比较接近，二者在流速、流向、高低潮流、转流等都基本一致。

3.3 水位检验

利用位于渤海的 QK 18－1、SZ 36－1、SZ 30－1和JZ 9－3共4个海洋石油开发区的现场水位实测资料对模拟结果进行了对比检验，结果见表3。从表3可以看出，模拟的水位与实际观测的水位吻合较好，二者之间的相对误差基本上都小于10%，相关系数基本上也都大于0.9。

表3 渤海水位现场实测和模拟计算的对比结果

上述对比检验结果表明，利用POM模式在渤海可以较精确地模拟海洋油气开发环境条件，模拟结果可以很好地反映渤海的海流和水位变化特征。基于此，利用该模式数值方法，以127mm×127mm的水平空间分辨率，给出了1985年1月1日至2004年12月31日20年来渤海不同海域海流和水位的逐时模拟结果，在此基础上找出了每年海流和水位年极值而组成连续20年的年极值序列，并利用Gumbel分布进行拟合后给出了渤海各水域的不同重现期的极端水位和流速（图2、3），从而为该区域油气田开发设计提供了依据。

4 结束语

结合海洋石油工程开发建设的实际需要，利用数值模拟方法开展渤海海洋环境条件参数计算，系统地考虑渤海海域的海洋环境特征，实现了从点到面的跨越，保证了计算结果的时空一致性，具有时空覆盖范围大、分辨率高、计算精度较高的特点。从技术方法上来说，这是一种很好的尝试，尤其是当工程海域海流调查资料稀缺或观测序列短，无法单纯利用观测资料完成海洋工程所需要的设计条件、一般作业条件以及疲劳条件的统计分析时，可以利用海流数值模拟技术进行环境条件计算，以满足海洋工程的需要。

［1］ 游小宝，李荣凤.海洋环流模式的发展和应用Ⅱ.近海和区域环流模式［J］.大气科学，2003，27（4）：729－739.

［2］ 张学洪，俞永强，刘海龙.海洋环流模式的发展和应用Ⅰ.全球海洋环流模式［J］.大气科学，2003，27（4）：178－188.

［3］ 赵艳玲，张铭，司广宇.海洋环流模式研究回顾与展望［J］.解放军理工大学学报：自然科学版，2006（3）：81－90.

［4］ BIUMBERG A F，GOMEZ－REYERS E，MUNASINGHE L.3D hydrodynamic model verification using ADCPS［C］.Hydr.Eng.，ASCE，1991：722－727.

［5］ 万振文，乔方利，袁业立.渤、黄、东海三维潮波运动数值模拟［J］.海洋与湖沼，1998，29（6）：611－616.

［6］ 李东辉，张铭，王纯富.海洋环流数值模式中的若干技术问题评述［J］.解放军理工大学学报：自然科学版，2003（4）：78－83.

［7］ BIUMBERG A F，MELLOR G L.A simulation of the circulation in the Gulf of Mexico［J］.Israel Journal of Earth Sciences，1985，34：122－144.

［8］ CHU P C，EDMONS N L，FAN C.Dynamical mechanisms for the South China Sea seasonal circulation and thermohaline variabilities［J］.Phys.Oceanogr.，1999，29：2971－2989.

［9］ 赵保仁，方国洪.渤、黄、东海潮汐潮流的数值模拟［J］.海洋学报，1994，16（5）：1－10.

［10］ 容新尧，杨修群.全球海洋环流模式中上层海洋对表面强迫的响应和调整Ⅱ.年代际变率［J］.海洋学报，2005（3）：21－32.