基于解析模型预测控制的欠驱动船舶路径跟踪控制器设计

，，，

(1.上海交通大学 船舶海洋与建筑工程学院，上海 200240；2.上海振华重工(集团)股份有限公司海上重工设计研究院，上海 200125；3.天津大学 建筑工程学院，天津 300072)

船舶路径跟踪控制是指在自动控制系统的作用下，船舶能从任意初始位置驶入预先设定好的参考航行路径，并沿此路径最终到达目的地，该参考航行路径与时间无直接关系[1]。欠驱动船舶路径跟踪控制系统具有强非线性、欠驱动、容易受到外界干扰影响等特点，是一个典型的非线性控制系统；对其进行研究有助于解决船舶在复杂环境中的操纵控制、自动靠离泊、海上装卸等实际问题。目前，关于欠驱动船舶路径跟踪控制的理论研究已取一定成果[2-4]，使得欠驱动船的跟踪并最终稳定在给定的参考路径。

本文主要针对欠驱动船舶路径跟踪控制中存在的风、浪、流等外界干扰，基于重定义输出、解析模型预测控制、非线性观测器技术，提出一种鲁棒跟踪控制算法。

1 问题的提出

考虑如下风、浪、流干扰的欠驱动船舶路径跟踪控制系统：

(1)

式中：x,y——船舶在固定坐标系中的平面位置；

u,v——船舶对水前进及横移速度，假设u为常数；

ψ,r——船舶航向角与转艏角速度；

Vc,ψc——固定坐标系中的流速、流向，假设Vc,ψc为常数，即均匀流；

mii——船舶惯性矩阵的对角线元素，包括水动力附加质量,i=1,2,3；

dii——横移、艏摇方向上的水动力粘性项,i=2,3；

τr——控制输入；

τwr(t)——由风、浪引起的有界干扰信号，满足τwr(t)≤τwr max<∞；

z1、z2、z3——系统输出。

控制目标是设计控制器τr使得欠驱动船舶在风、浪、流等外界干扰的影响下能够跟踪给定的参考路径。

式(1)中船舶在平面内的位置和运动参数的关系也可写为

(2)

其中船舶对地运动速度与对水运动速度间的关系为

(3)

将船舶运动模型转化到Serret-Frenet标架内进行研究[5]，见图1。

图1 欠驱动船舶路径跟踪控制系统

(4)

式中：c(s)——曲线曲率。

(5)

令：

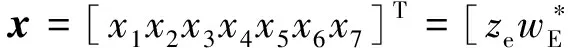
得到Serret-Frenet标架下的欠驱动船舶路径跟踪控制系统模型。

(6)

2 路径跟踪控制器设计

应用解析模型预测控制与非线性观测器联合控制的方法[6]，经过推导整理，得到风、浪、流干扰下的欠驱动船舶路径跟踪控制律。

3 计算机仿真结果

通过计算机仿真来验证欠驱动船舶路径跟踪控制律的有效性。选用的实船参数为[5]

船长32 m,质量118×103kg；

m11=120×103kg；m22=217.9×103kg；

m33=636×105kg·m2；d22=117×103kg/s；

d33=802×104kg·m2/s；

船舶前进速度u=10 m/s；

预测周期T=25 s； 控制阶次l=6。

计算得到k0=0.821 3,k1=1.54。选取常数k=0.2, 增益p0=5×105。

有界干扰τwr(t)为

(7)

式中：rand(·)——最大幅值为1的随机干扰信号。

均匀流Vc=4 m/s,ψc=2 π/9 rad。参考路径选取为以原点为圆心、半径为80 m的圆。初始条件为

x(0)=100 m,y(0)=0 m,ψ(0)=π/9 rad,

v(0)=1 m/s,

ua(0)=10+4×cos(π/9)=13.76 m/s,

va(0)=1+4×sin(π/9)=2.37 m/s,

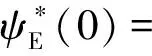
-1.05 rad,r(0)=0 rad/s。

仿真结果见图2～5。

图2 欠驱动船舶路径跟踪轨迹

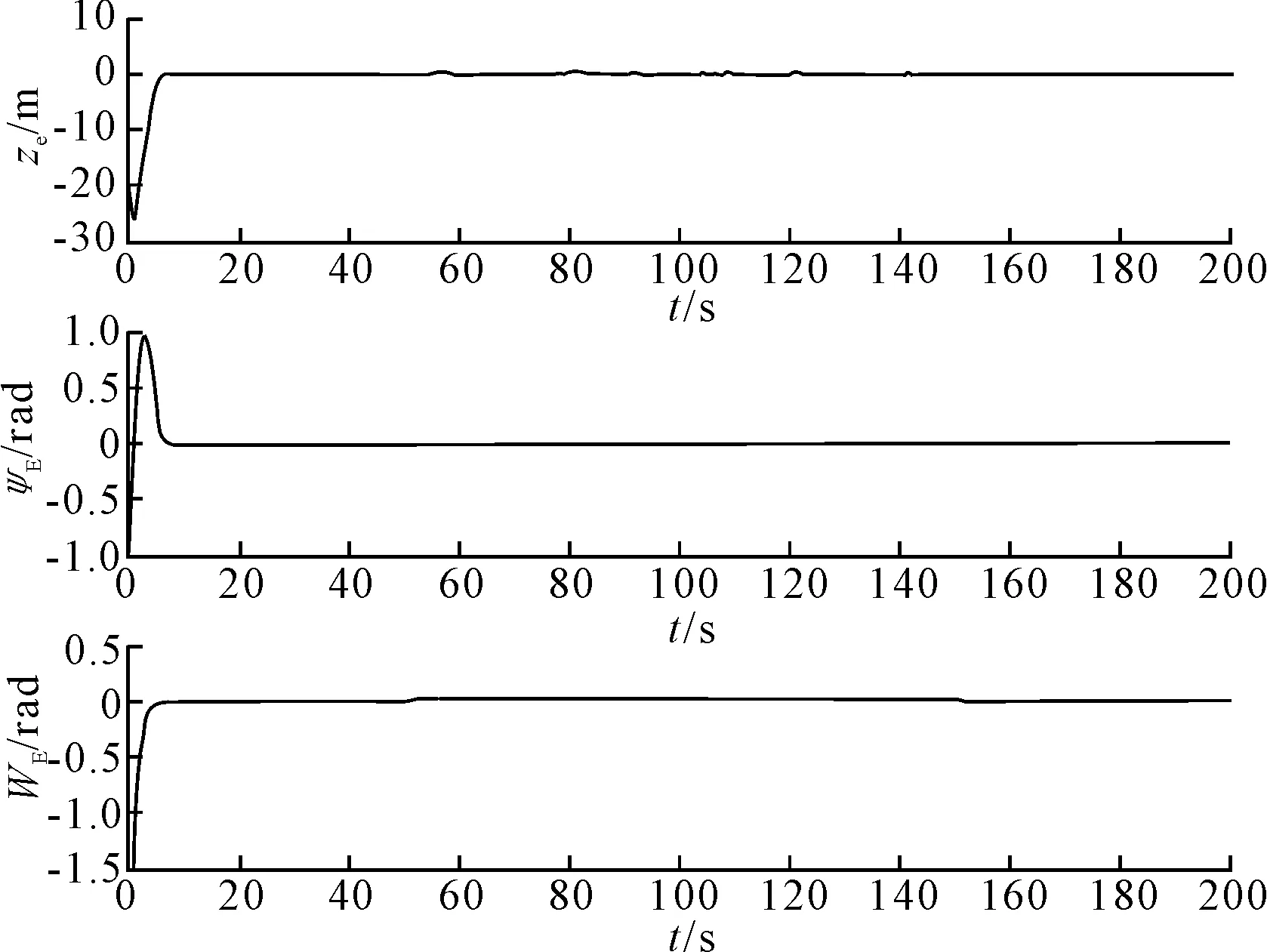
图3 路径跟踪误差ze、以及重定义输出

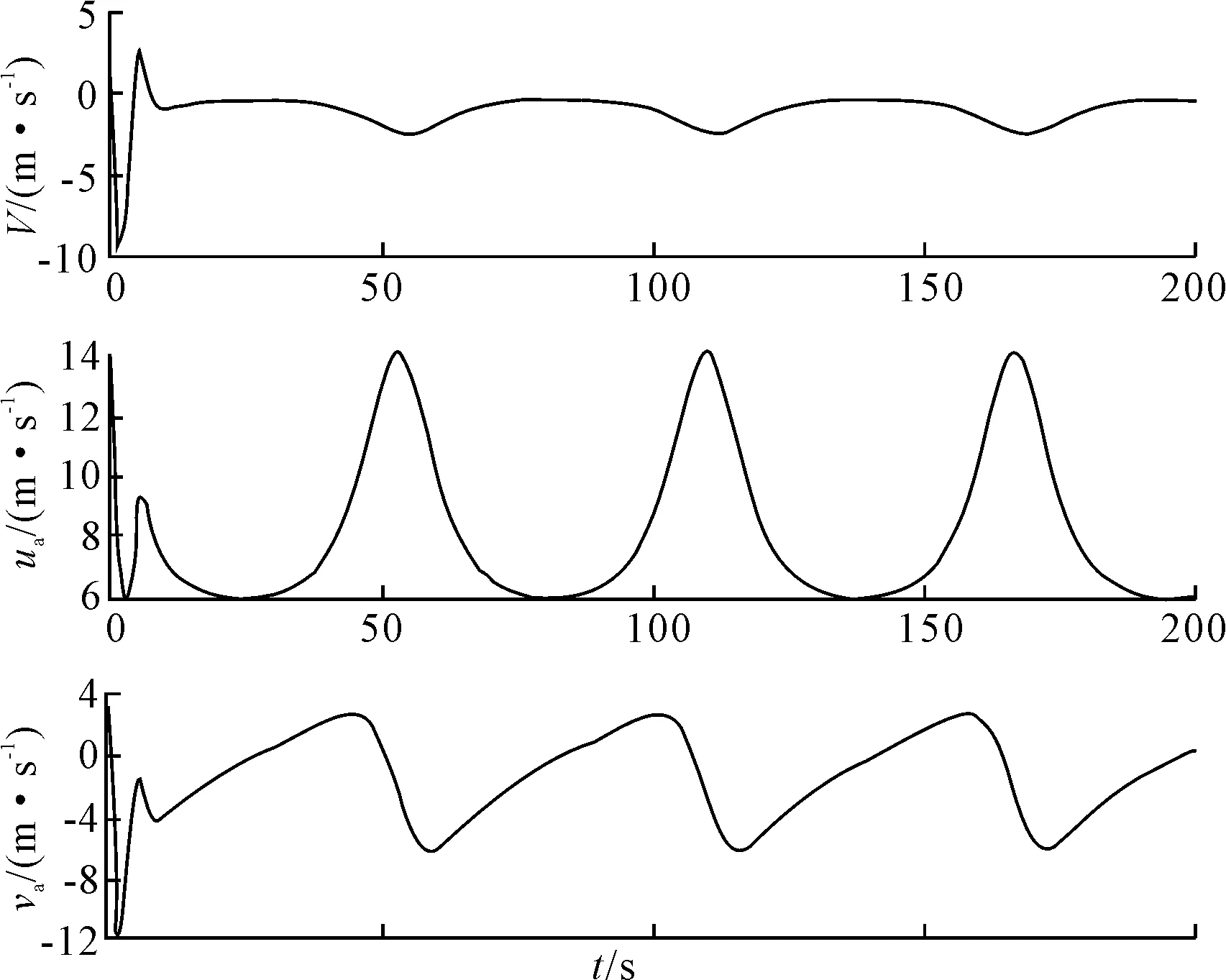
图4 船舶的相对速度v 以及绝对速度ua、va

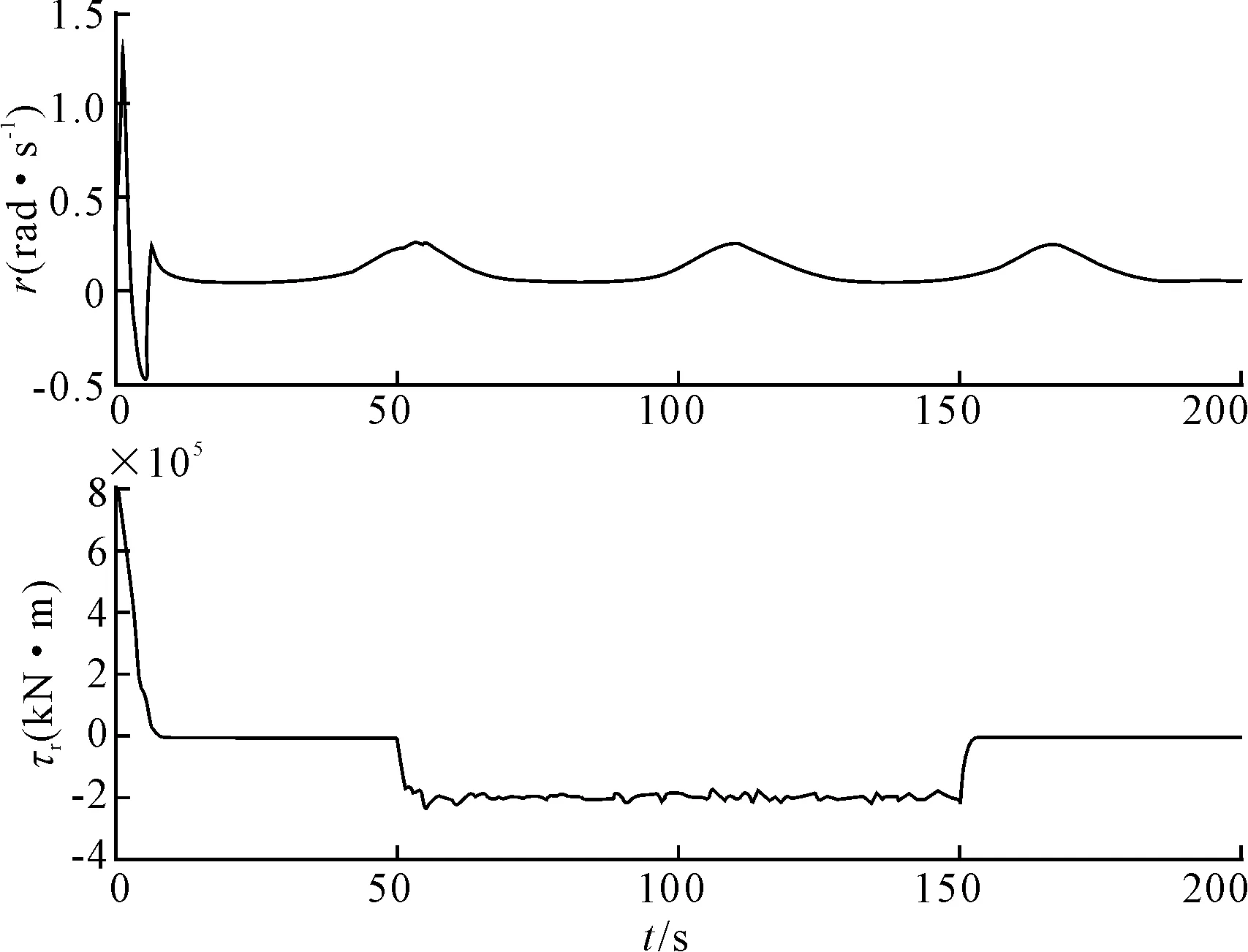
图5 转艏角速度r以及控制力矩τr

图2表示欠驱动船舶在控制律式(7)作用下的路径跟踪轨迹。从图2可以看出，欠驱动船舶能够抵抗风、浪、流干扰的影响，最终跟踪并稳定在给定的参考路径上。图3表示路径跟踪的位置误差、角度误差，以及代表二者组合形式的重定义输出。从图3中可以看出，在干扰的影响下，跟踪误差会有较小波动，最终会收敛到零值。图4～5表示船舶速度、转艏角速度以及控制力矩的历时曲线。

4 结论

将船舶运动模型转化到Serret-Frenet标架内进行驱动船舶在风、浪、均匀流干扰下的路径跟踪控制问题研究，并引入重定义输出，将原控制系统转化为单输入单输出控制系统，简化了控制器的设计。应用解析模型预测控制与非线性观测器方法设计了欠驱动船舶路径跟踪控制器，该控制器类似于一种非线性PID控制算法，使得欠驱动船舶在控制器的作用下，能够抵抗风、浪、均匀流的影响，使路径跟踪误差收敛到零，跟踪并最终稳定在给定的参考路径上。计算机仿真实验验证了所提算法的有效性。

[1] ENCARNACAO P,PASCOAL A.Combined trajectory tracking and path following: an application to the coordinated control of autonomous marine craft [C]∥Proceedings of the 40th IEEE Conference on Decision and Control,Orlando,Florida USA,2001:964-969.

[2] PETTERSEB K Y,NIJMEIJER H.Underactuated ship tracking control: theory and experiments [J].Int.J.Control,2001,74(14):1 435-1 446.

[3] ZHANG R J,CHEN Y B,SUN Z Q,et al.Path control of a surface ship in restricted waters using sliding mode [J].IEEE Transactions on Control Systems Technology,2000,8(4):722-732.

[4] 李铁山，杨盐生，郑云峰.不完全驱动船舶非线性控制[J].交通运输工程学报，2003,3(4)：39-43.

[5] CHEN W H,BALANCE D J,GAWTHROP P J.Optimal control of nonlinear systems: a predictive control approach [J].Automatica,2003,39(4):633-641.