水下爆炸气泡射流作用下固支方板动态响应的数值仿真研究

2012-01-23，，，

船海工程 2012年1期

，，，

(1 海军航空工程学院研究生管理大队，山东烟台 264001；2海军工程大学船舶与动力学院，武汉 430033)

传统上将水下爆炸载荷分为两个阶段：冲击波阶段和气泡阶段。冲击波载荷能够对舰船结构造成严重的局部毁伤，而气泡载荷主要引起舰船结构的整体毁伤，当气泡脉动周期与舰船低阶振动频率接近时可能引起舰船结构的“鞭状响应”(Whipping)[1]，当气泡尺寸较大时可能造成舰船浮力损失，进而造成整体破坏[2]。药包在结构近场爆炸时，气泡受到结构等边界影响容易形成射流，射流载荷也可能对结构产生毁伤作用。对于水下爆炸气泡运动及其塌陷形成射流的过程已有很多研究[3-4]，在射流形成的条件、射流的影响因素等问题上取得了很多研究成果。但是国内关于由射流载荷引起的结构毁伤研究尚不多见。研究射流载荷引起的固支方板毁伤的特点、程度等问题对舰船防护设计和水中兵器战斗部设计具有重要的军事意义及参考价值。为此，模拟近水面处水下爆炸气泡的脉动及产生射流的过程，并得到相应的固支方板结构的动态响应。

1 基本理论

1.1 欧拉算法简介

对于水中爆炸问题，采用欧拉方法求解比较合适。当采用欧拉方法时，节点固定在空间中，由相关节点连接而成的单元仅仅是空间的划分，分析对象的材料在网格中流动，材料的质量、动量和能量从一个单元流向另一个单元。见图1。

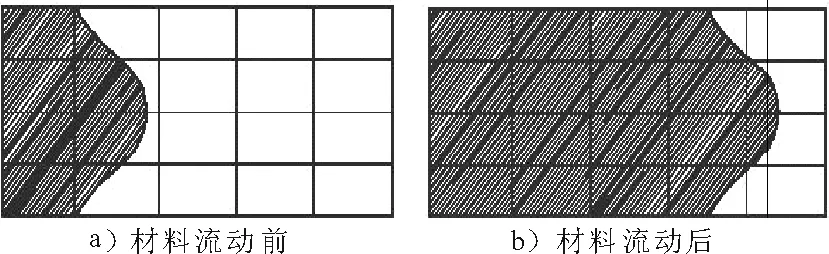
图1 Euler求解器中的网格

欧拉材料在单元之间的流动主要用质量守恒、动量守恒和能量守恒来描述。

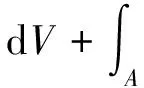
(1)

(2)

(3)

式中：V——体积；

A——该体积区域的边界；

n——边界上的法向量；

u——区域内速度向量。

物质从一个单元传递到另一个单元，输出单元和输入单元都可以包含多种欧拉材料，每个欧拉单元最多可以有五种材料。

1.2 材料状态方程

在水下爆炸问题的仿真研究中涉及空气、水、炸药及金属。各种材料本构关系选取是否恰当，直接关系到计算结果的精度。

仿真计算中认为空气是理想气体，并且满足

p=(γ-1)ρ·e

(4)

式中：p、ρ、e——气体的压力、密度和比能；

γ——气体比热比。

认为炸药是高度压缩高压气体，也适用式(4)。

假设水是无粘无旋的可压缩流体。其压力状态方程用多项式表示为

(5)

式中：k——体积模量；

ρ、ρ0——总密度和参考密度。

金属材料的模拟采用双线性弹塑性本构模型，材料的屈服极限σy描述为

εp

(6)

式中：σ0——静态屈服强度；

Eh——应变硬化模量；

εp——有效塑性应变。

材料在强冲击载荷作用下，一般会产生比较明显的应变率强化效应，特别是对于低碳钢这种应变率敏感材料。计算中应变率强化模型采用Cowper-Symonds模型，动态屈服强度σd为

(7)

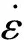
C、P——应变率系数，对于低碳钢,一般取C=40，P=5。

材料失效模型采用最大塑性应变失效。

2 数值仿真模型

模型区域尺寸为3.0 m×3.0 m×2.4 m，见图2。其中上面0.4 m为空气，下面2.0 m为水。在模型中，结构与炸药有两种相对关系，炸药在结构底部和侧面，可以很好地代表船底和舷侧两种典型舰船局部结构。炸药正对固支方板的中心点，底部爆炸爆距分别为0.2 m和0.1 m，侧面爆炸爆距分别为0.20、0.15 m。

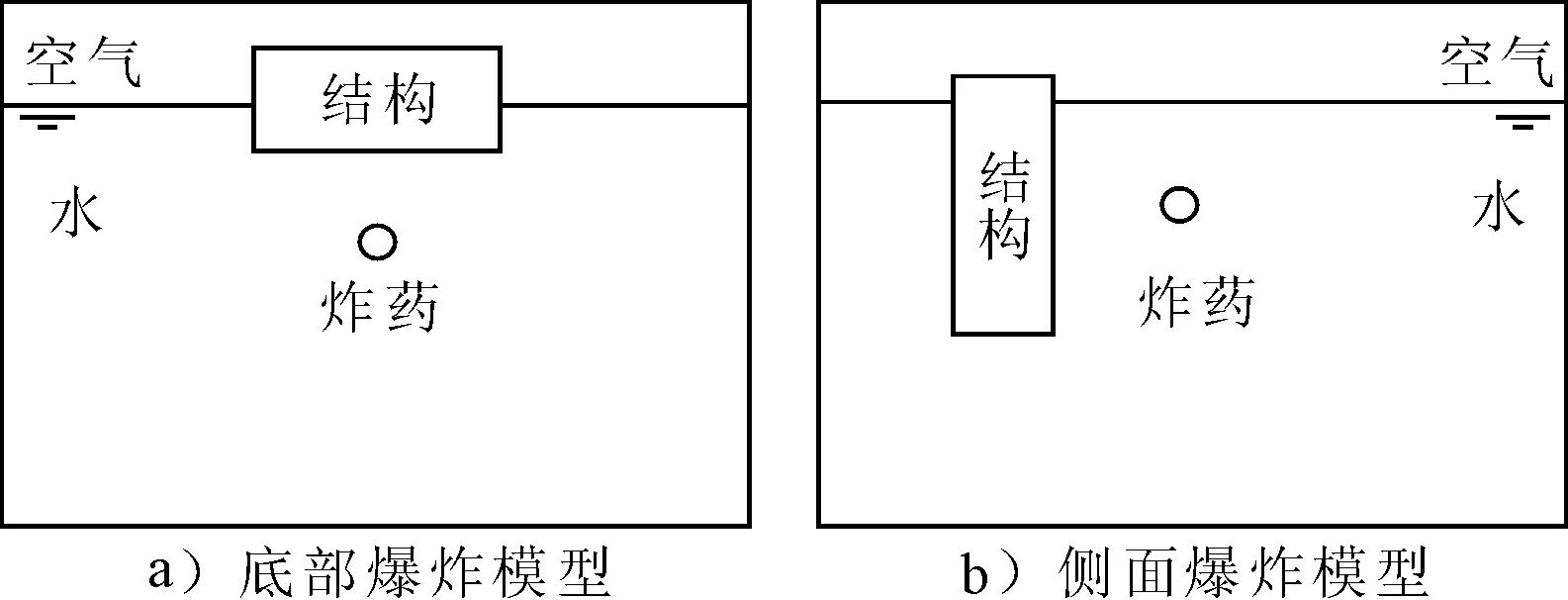
图2 炸药、水面与结构位置关系

水和空气采用欧拉正六面体单元划分，单元尺寸为0.05 m，共计172 800个欧拉单元。固支方板指方板在边界处沿x、y、z三个方向上的位移和弯矩都为零，方板边长为1.0 m，采用拉格朗日四边形单元划分，单元尺寸为0.016 7 m，共计3 600个拉格朗日单元。为了使耦合面成为封闭曲面，且计算过程中耦合面内体积不能为负，建立了9 360个“哑单元”。“哑单元”是虚拟单元，只起到封闭耦合面的作用，不影响结构响应。计算中采用一般耦合算法，耦合面取结构和“哑单元”组成的封闭曲面。

欧拉区域上表面压力为101.33 kPa，下表面为121.38 kPa。水的密度取1 000 kg/m3，体积模量为2.2 GPa。空气密度1.21 kg/m3，比热比取为1.4，比能取210 kJ/kg，初始压力为100 GPa。TNT炸药密度为1 580 kg/m3，炸药重5 g，比能为4 190 kJ/kg。在MSC.Dytran中炸药可以用JWL或者高压气体方程来模拟，若假设药包为球形，药包半径不足0.01 m，比欧拉网格尺寸小太多，在计算中会影响精度，因此在计算中取半径为0.02 m，按照总能量守恒原则，其密度相应调整为149 kg/m3。按照理想气体状态方程计算，炸药初始压力为250 MPa。

方板结构模型材料计算采用双线性强化模型,材料参数参照文献[5]。弹性模量取为210 GPa，泊松比为0.3，密度为7 800 kg/m3，强化模量为250 MPa，静态屈服极限为250 MPa，最大失效应变为0.2。

3 仿真结果及分析

3.1 气泡运动仿真结果

整个计算时间为100 ms，底部爆炸仿真和侧面爆炸仿真清晰地再现了气泡运动并发生射流的现象。图3和图4显示了炸药爆炸时气泡膨胀、收缩并发生冲向结构的射流的全过程。底部爆炸和侧面爆炸在气泡膨胀阶段基本相似，但是在气泡收缩阶段侧面爆炸比底部爆炸更早发生射流。侧面爆炸气泡脉动周期与自由场相比相差不大，底部爆炸时气泡脉动周期变长。

图3 底部0.1 m爆炸气泡运动过程

图4 侧面0.15 m爆炸气泡运动过程

3.2 射流速度计算结果

仿真发现，气泡在塌陷形成射流时，流体质点速度很大，最高可以达到200 m/s，但是到达结构处流体质点剩余速度一般在40～50 m/s这一量级。图5给出了射流发生时，结构附近流场质点速度矢量。从方向看，射流发生时周围流体都向着板中间方向运动。对于底部和侧面爆炸，发生射流时质点运动情况基本类似。

3.3 结构响应计算结果

从结构响应角度来看，冲击波载荷过后，结构整体有比较大的塑性变形，射流载荷过后，板的中心塑性变形挠度增加较大，对周围区域塑性变形影响不大。这与以上分析射流发生时流体质点运动特点相吻合。射流时，质点都被气泡聚集在一起向结构中心运动，引起较大局部变形。图6是底部0.20 m爆炸时结构等效塑性应变云图。可以看出，冲击波载荷过后，中间很大区域形成一个平台，而射流载荷过后，应变和变形梯度增大。侧面爆炸时，情况基本一致。

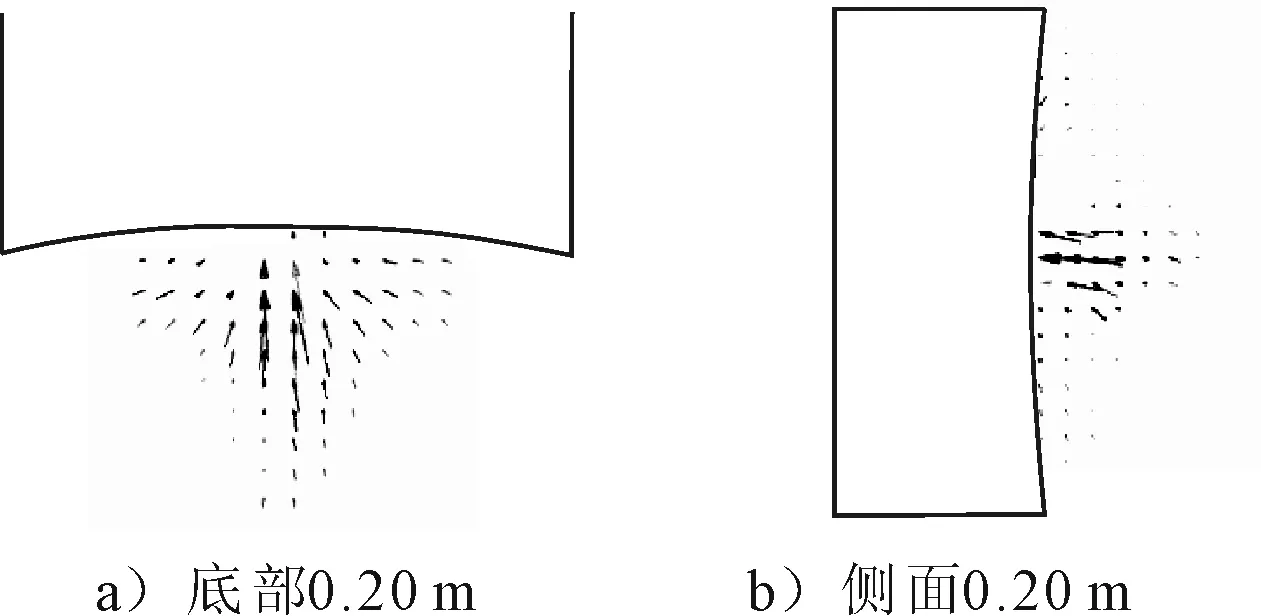
图5 射流发生时结构附近流体节点速度矢量

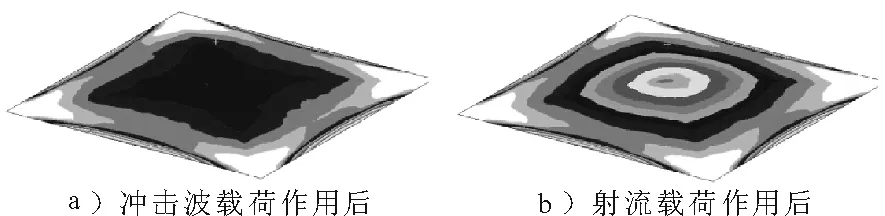
图6 等效塑性应变云图

为准确研究结构上不同位置点的变形特点，在结构上取4个典型点A、B、C、D，见图7a)，其中A为整个结构中点，其余3个点沿中心线等间距分布。

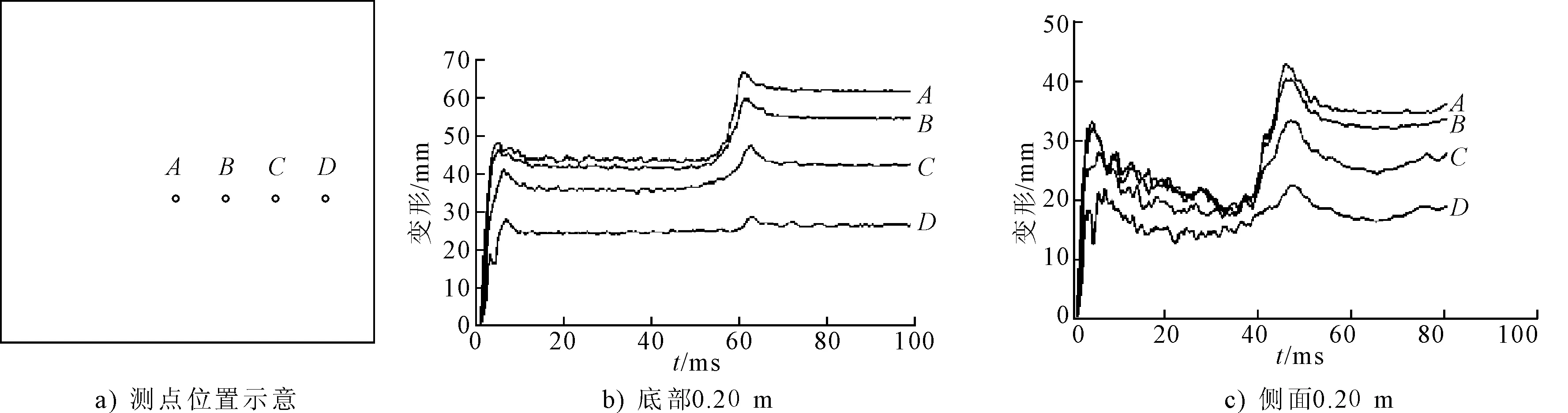
图7 典型位置变形挠度随时间变化曲线

图7显示结构的变形明显分为两个阶段，前一阶段是由冲击波载荷引起的，后一阶段是由气泡射流引起的。还可以看出，冲击波载荷引起中间很大区域形成一个平台，而射流载荷引起变形梯度增大。各点的塑性变形挠度见表1中。

从总变形来看，底部爆炸要比侧面爆炸变形大，但是射流引起的塑性变形在总变形中所占的比例基本相同，在射流发生的部位该比例超过30%；中间点射流引起的变形所占比例比较大，靠近固支边的位置受射流影响较小，这说明射流的影响区域很小，主要引起射流区域附近结构的变形，这与冲击波和气泡脉动压力载荷引起的塑性变形是不同的，压力波引起的变形区域比较大。