基于Monte Carlo方法的舰船装备系统任务成功概率模型
2012-01-23,,
,,
(海军工程大学 动力工程系,武汉 430033)
任务成功概率(mission completion success probability,MCSP)定义为在规定的任务剖面内,装备系统能完成规定任务的概率,是任务成功性最根本的度量指标[1]。MCSP不仅与装备自身的可靠性、维修性、使用环境、任务要求等因素相关,还与维修保障密切相关,因此该指标对装备使用和指挥决策,以及维修保障决策均具有很强的指导性。基于此,系统的MCSP模型一直是研究的热点,但纵观现有的相关研究[2-5],由于多是假设系统组成单元的寿命或故障间隔时间服从指数分布,没有考虑单元已工作时间对系统MCSP的影响,且认为使用同类备件的单元的寿命也同分布,因而所建模型对于多为老装备,且寿命或故障间隔时间多为非指数分布的舰船装备而言,适用性较差。因此,本文基于Monte Carlo方法,建立综合考虑系统组成单元独立但不同分布,且寿命可为任意分布情况下的MCSP模型。
1 问题描述
对于舰船系统而言,由于受海上维修条件所限,维修工作主要是更换备件,MCSP与备件数量密切相关,另外,尽管舰船装备系统十分复杂,但最终总能简化为由多个串联或并联子系统所构成的串联系统,因此,计算舰船装备MCSP的关键在于计算有限备件保障下串联和并联系统的MCSP。
2 假设
1) 故障均可通过更换备件予以排除,不考虑因无法维修而导致的任务失败,即任务成功与否仅与是否有足够备件相关。
2) 忽略更换备件的时间,这是因为若装备设计为可通过更换备件排除故障时,换件时间通常很短,与任务时间相比可忽略不计。这样,连续无间断工作的任务要求就转换为装备及其所携带的备件的总工作时间能超过任务时间的要求。
在上述假设成立的前提下,对于要求系统连续工作的任务,系统的MCSP等价于在给定备件保障条件下系统的持续工作时间大于任务时间的概率。对于单个单元,当假设备件在储备期内不发生失效时,可根据冷储备系统的理论计算其MCSP[6];但是,对于由同类备件保障的串联或并联系统,当单元的寿命不服从指数分布时,很难建立系统的MCSP解析计算模型。因此,本文重点研究串联和并联系统的MCSP数值计算模型。
3 系统MCSP模型
3.1 串联模型
系统由n个单元串联而成,单元i的寿命为随机变量Xi,任务前累积已工作时间为t0i,各单元相互独立但不一定同分布,所有单元的故障均可通过更换同类备件予以排除。现在的问题是:当系统由m个该类备件保障、执行时间为T的任务,系统的任务成功概率为多少。
显然,当m=0时,系统的寿命等于原串联系统的寿命,即n个单元的寿命的最小值,记原串联系统的寿命为Y0,原串联系统与m个备件组成的新系统的寿命为Xs,则
(1)
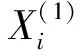
(2)
依次类推,带m个备件时,由原串联系统和m个备件构成的新系统的寿命等于m+1个串联系统的寿命之和,从而
(3)
上式除指数分布因具有“无记忆”特性可以直接求解外,对于其它分布,由于剩余寿命的分布函数发生变化,直接求解十分困难,因此,利用Monte Carlo抽样技术进行数值求解[7]。其计算步骤如下。
1) 利用抽样公式得到各单元寿命的样本值xi,从而原串联系统寿命的样本值为y0=min(x1,x2,…,xn),寿命样本值等于y0的单元为故障单元。这里,若考虑原工作单元的已工作时间,抽样公式采用剩余寿命抽样公式;
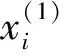
3) 根据故障单元编号,可标记各单元已工作时间,从而利用剩余寿命抽样公式可依次得到y2,…,ym,这样就得到了Xs的样本值xs,若xs>T,任务成功,否则任务失败;
4) 将1)~3)的计算过程重复N次,根据概率论的理论,当N足够大时,N次计算过程中任务成功的总次数与N的比值即为任务成功概率的近似值。
其中,第j次更换备件后,单元i已工作时间t0ij为
t0ij=t0i(j-1)·pij+yj-1
(4)
式中:t0i(j-1)——第j-1次更换备件后单元i的已工作时间;
pij——第j次更换备件时单元i的状态变量,若i故障,pij=0,否则pij=1。
3.2 并联系统MCSP模型
对于并联系统,由于一个单元故障并不导致系统故障,因此在更换备件时有多种策略,比较典型的两种换件策略是:单元故障时换件和系统故障时换件。由于换件时机不同,系统的MCSP计算方法也有所不同。
3.2.1 单元故障时换件的策略
需解决的问题与串联系统类似,不同的是单元之间为并联关系,采取的换件策略是一旦有单元发生故障且还有可用备件,立即更换备件并继续投入工作。
当m=0时,系统的寿命等于原并联系统的寿命,采用与串联系统分析中相同的符号,则有
Xs=max(X1,X2,…,Xn)
(5)
当m=1时,由于采取了有单元故障就换件的策略,因此原并联系统与1个备件构建的新系统的寿命相当于由两部分合成。若将更换故障单元的时刻作为并联系统的一次寿命终结,则新系统的寿命等于一个串联系统与一个并联系统的寿命之和,即
Xs= min(X1,X2,…,Xn)+
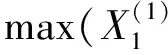
(6)
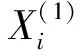
依次类推,原并联系统与m个备件构建的新系统的寿命相当于m个串联系统与一个并联系统的寿命之和,即
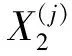
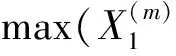
(7)
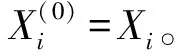
同样,对上式也只能利用Monte Carlo抽样技术进行求解,其算法如下。
1) 利用抽样公式得到并联系统各单元寿命的样本值Xi,从而原并联系统寿命的样本值为y0=max(x1,x2,…,xn),各单元寿命的最小值z0=min(x1,x2,…,xn),寿命样本值等于z0的单元为故障单元。
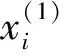
3) 按同样的方法,得到y2,…,ym,z2,…,zm,从而,m=0时,xs=y0;m>0时,xs=z0+z1+…+zm-1+ym,若xs>T,任务成功,否则任务失败。
4) 将1)~3)的计算过程重复N次,当N足够大时,N次计算过程中任务成功的总次数与N的比值即为任务成功概率的近似值。
其中,第j次更换备件后,单元i已工作时间t0ij的计算方法与串联系统一致。
3.2.2 系统故障时换件的策略
当采取系统故障才换件的策略时,即并联系统的n个单元全部故障才更换备件,最终可能会出现可用备件不足以更换整个并联系统的情况,此时的策略是有多少换多少。但由于各个单元的寿命不一定同分布,因此,更换的单元不同可能会导致MCSP的计算结果不同。为此,必须确定备件不足时的更换原则,无论何种原则,其计算方法是一致的。故不妨设最后一次更换按单元平均寿命从大到小的顺序进行。
假设备件数量与并联单元数量存在如下关系。
m=k×n+hk=0,1,2…
(8)
式中:h——小于n的正整数。
上式表明,m个备件可对并联系统进行k次整体替换,最后一次可更换原并联系统中的h个单元。根据前面的分析思路,在该更换策略下,由n单元并联系统和m个备件构建的新系统的寿命等价于k个n单元并联系统和1个h单元并联系统的寿命之和,即
Xs=k·max(X1,X2,…,Xn)+
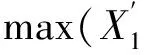
MCSP=P{k·max(X1,X2,…,Xn)+
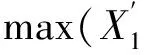
(9)
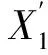
MCSP的数值算法与前述算法类似,对原并联系统的寿命进行k次抽样,对最后一次更换备件所得的并联系统进行1次抽样,累加这k+1个并联系统的寿命样本值,即可得到Xs的样本值。
4 示例
根据任务需求确定需投入的装备以及装备之间的逻辑关系,同时确定各装备的可更换单元,以可更换单元作为计算装备系统MCSP的独立单元。
按照只要通用同类备件就归为同类单元的原则,并结合装备之间的逻辑关系,确定装备系统的结构函数F。不失一般性,假设A、B、C类单元分别由A、B、C类备件保障。
F=A·B1·B2·(C1+C2)
(10)
最后确认计算所需的初始数据,见表1。为简化表述,假设各单元的寿命(h)均为威布尔分布。
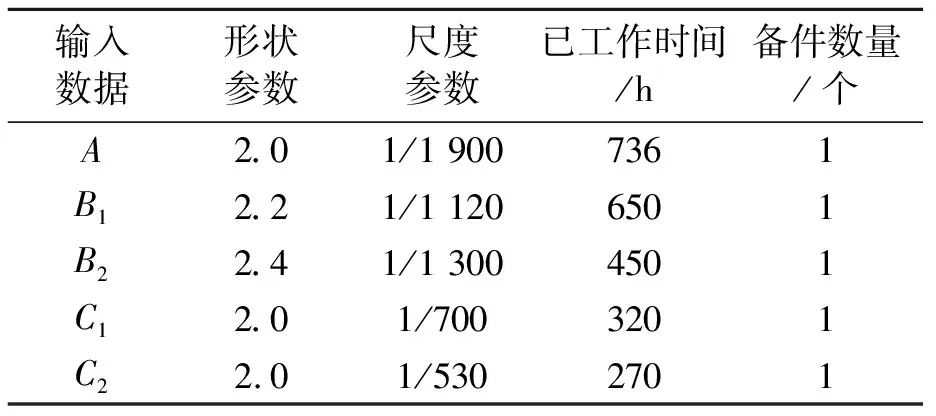
表1 算例所需的输入数据
完成上述工作后,即可利用文中给出的串并联系统MCSP算法计算舰船装备系统的MCSP。假设任务时间为360 h,并联系统采取单元故障时换件的策略,取N=10 000,计算结果为
MCSPA=0.997 8,
MCSPB=0.907 3,
MCSPC=0.915 9。
从而有
MCSPSYS=MCSPA·MCSPB·MCSPC=
0.829 2。
5 结论
舰船装备是一个十分复杂的系统,装备之间的负载分担、相关失效以及装备自身的多状态和多功能等诸多复杂特性都对系统的任务成功性存在影响。因此,要准确计算舰船装备的任务成功概率,还有待于在充分考虑上述复杂特性的基础上进一步展开深入研究。
[1] 殷鹤龄.可靠性维修性保障性术语集[M].北京:国防工业出版社,1990.
[2] 张 泉,张 涛,郭 波,等.有限备件条件下系统任务成功概率的求解算法[J].系统工程,2004,22(11):95-98.
[3] 郭 波,张 涛,张 泉,等.备件组合方案下的多阶段任务成功性评估模型[J].系统工程理论与实践,2005(2):94-99.
[4] SCHEEWEISS WNIFRID G.Mission success with components not as good as new [J].Reliability Engineering and System Safety,1996,52: 45-53.
[5] 刘 芳,赵建印,郭 波.可修系统任务分析与成功性评估模型[J].系统工程与电子技术.2007,29(1):147-150.
[6] 曹晋华,程 侃.可靠性数学引论[M].北京:高等教育出版社,2006.
[7] 杨一民,盛一兴.系统可靠性数字仿真[M].北京:北京航空航天大学出版社,1990.
