对几种损伤识别方法的噪声敏感性分析

,

(中国海洋大学 工程学院，山东 青岛 266100)

由于结构试验测试技术有限、大型复杂结构周边环境复杂以及测量过程中不确定干扰多等因素，导致土木结构响应的实测数据必然受到噪声干扰。由于相对较大的噪声干扰，导致很多在航空航天领域以及机械制造领域非常有效的损伤识别方法应用于工程结构时却几乎失效。基于动力测试的损伤识别，当测试信号或由测试而得到的模态有误差时将影响识别精度，测试噪声及各种环境不确定性干扰所导致的模态参数识别精度不高是制约损伤识别技术走向实用化的关键问题之一，能否在噪声条件下具备良好的鲁棒性是测试方法最终应用于工程实际的一个关键因素。

通过分析常用的一些损伤识别指标，考虑到噪声干扰的随机性及损伤特征的稳定性，根据结构的构造特点与动力特性确定合适的结构损伤定位指标。对4种结构损伤定位指标的抗噪声干扰能力进行对比分析。

1 基本理论

1.1 损伤识别方法

任何结构都可以看作是由刚度、质量、阻尼矩阵组成的力学系统，结构一旦出现损伤，结构参数也随之发生改变，从而导致系统的频响函数和模态参数(固有频率、阻尼和振型等)发生改变。所以，结构模态参数的改变可视为结构损伤发生的标志。由此选取常用的四种损伤识别指标进行抗噪声能力检验。

模态参数对柔度矩阵的贡献与固有频率的平方成反比，模态试验中只需获得较低阶模态参数，就可较好地估计结构柔度矩阵。常用的基于柔度矩阵的损伤识别方法中，利用中心差分法对柔度求出二阶导数，即柔度差值曲率[1]，对悬臂梁及简支梁等结构有较好的识别效果。

模态应变能法的基本思想是将结构分解为一系列的单元，计算结构损伤前后每个单元的模态应变能变化，而部分模态振型在结构损伤附近发生局部突变，故模态应变能在结构中的分布将发生变化。所以，可以通过比较每一单元模态应变能的变化来进行结构损伤诊断[2-4]。

1.2 噪声的施加方式

在目前的结构损伤识别方法中，基本以两种方式模拟噪声[5]：在仿真振动信号上加噪声，用信噪比SNR表示噪声水平大小；在模态分析得到的模态参数上加噪声。

研究中用有限元程序得到的模态参数来模拟实际结构无测试误差的模态参数真值，采用Matlab标准正态分布随机数来模拟测试误差，对几种损伤识别指标的噪声敏感性进行分析。

xi=x(1+ε·η)

(1)

式中：xi——加入随机噪声后的值；

x——振型的真实值；

ε——噪声水平；

η——具有零均值、单位标准差的正态分布随机变量(高斯白噪声)。

2 数值算例

2.1 简支梁结构损伤诊断数值算例

简支梁结构尺寸：截面宽b=0.25 m，截面高h=0.2 m，梁长L=6 m，材料弹性模量32 GPa，材料密度2 500 kg/m3。该简支梁被均分为20个单元，其单元号及节点号见图1。

图1 简支梁有限元模型

在损伤分析中，通过降低单元材料弹性模量的大小来改变刚度以模拟各种损伤工况，具体损伤情况见表1。

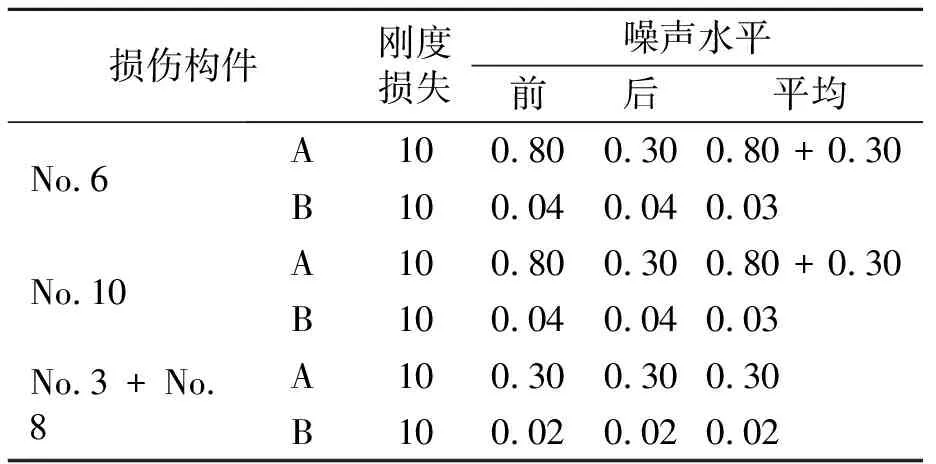
表1 简支梁损伤定位识别结果 %

注：A为改进后的模态应变能法；B为柔度差值曲率法。

分别对比模态振型不加噪声、损伤前模态振型加噪声、损伤后模态振型加噪声、损伤前后模态振型均加噪声4种情况。由于噪声引入了随机因素，因此用统计的方式考虑噪声影响后的模态参数。文中所有算例中的模态参数均是在相同噪声水平下，随机取50次，然后取平均结果。临界噪声水平指仍能正确识别出损伤单元位置，但对未损伤单元有误判，且由于噪声的随机性，误判值及误判数量并没有明显的规律可循[6]。

可以看出，对于一维简支梁，在没有模态噪声的情况下，都能很好地进行模态识别，但施加噪声后，在刚度损失10%时，柔度差值曲率法仅能承受0.04%左右的噪声水平，改进后的应变能法抗噪性更强。采用柔度差值曲率法时，对一些构件，损伤前模态能承受更高的噪声水平。

2.2 三维框架模型结构损伤诊断数值算例

选取一个三维框架结构模型作为研究对象，见图2。该框架结构为5层、24个结点、40个单元。该框架结构层高1 m，长跨长3 m，短跨长1 m，结点1、2、3和4固定于地面。所有的梁和柱具有一样的截面尺寸。结构模型共分成40个单元。

图2 三维框架结构

损伤工况及识别结果见表2。由于模态应变能法假定结构的振动变形以弯曲为主。对于三维复杂结构,其主要构件(例如桩)以弯曲变形为主,但水平撑、斜撑构件以轴向拉压变形为主,直接利用此损伤诊断指标定位失效。可以看出，不同构件的抗噪性是不同的，而那些存储模态应变能较少的单元，往往比较敏感。对于此模型结构，两种方法对柱构件(No.20)都有较强的抗噪性。改进后的模态应变能指标对损伤前模态能承受更高的噪声水平，CMCM指标由于使用损伤前有限元的全阶模态，故能对损伤前模态承受较高的噪声水平。而对损伤后模态噪声较为敏感。

表2 三维框架结构损伤定位识别结果 %

注：A为改进后的模态应变能法，B为CMCM, C为模态应变能法(下同)。

2.3 Benchmark结构损伤诊断数值算例

Benchmark结构研究问题首先是由美国土木工程协会(ASCE)的结构健康监测研究小组提出的。图3所示的结构是一个4层、2×2跨的钢结构缩尺模型[7]。本节数值算例是基于Benchmark结构的有限元模型，使用的模态参数是通过有限元模型特征值分析得到的，其构件材料特性参数见表3，弹性横量均为2×1011Pa。

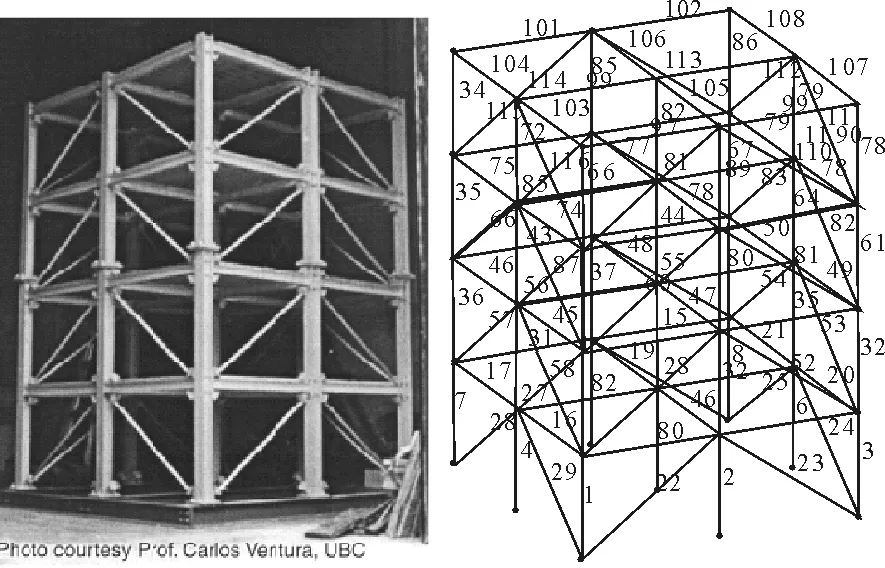
图3 Benchmark结构框架模型及有限元模型

表3 Benchmark结构构件材料特性参数

由于柔度差值曲率法仅适用于一维结构，对Benchmark结构选取模态应变能法、改进后的模态应变能法和CMCM进行对比,见表4。

表4 Benchmark结构损伤定位识别结果 %

可以看出，改进后的模态应变能法和CMCM能对柱、梁、斜撑均做出正确损伤定位，且有良好的抗噪性。由于三维结构构件增加，结构更加复杂，与一维简支梁数据对比，临界噪声水平下降。这表明，同一种方法，对不同结构的抗噪性需进一步具体分析。

2.4 海洋平台结构损伤诊断数值算例

通过模拟固定式钢质导管架海洋平台的结构特点，建立海洋平台结构的有限元模型，见图4。

图4 海洋平台结构框架模型及模拟损伤工况

该模型共4层，与基础固接。桩腿及桩模型尺寸为直径20×2，水平横撑及斜撑模型尺寸为直径10×2。对结构进行损伤识别，结果列于表5。

表5 海洋平台结构损伤识别结果 %

可以看出，随着损伤程度的增加，临界噪声水平随之增加，对于不同位置的构件，抗噪性是不同的，且损伤前模态能承受更高的噪声水平。

3 结论

在噪声干扰下，损伤区域的定位指标误判逐渐增大，直到被噪声引起的损伤指标变化所掩盖而失去定位能力。噪声干扰具有一定的波动性和随机性，应进行多次噪声样本的统计分析确定不同损伤指标正确识别损伤所对应的临界噪声水平，比较不同损伤定位指标的噪声鲁棒性。

对误差和噪声的敏感度分析既要考虑识别方法的抗噪性，又要考虑结构自身的特点，应将结构与方法相结合，对抗噪性进行进一步分析。分析结果表明，改进后的模态应变能法和CMCM方法对于一维结构和框架结构损伤定位具有较好的抗噪声干扰能力。对一些构件，损伤前模态能承受更高的噪声水平。需要指出，文中针对模态噪声对损伤识别的影响是第一步，可以为将来工程化实施应用提供分析筛选损伤指标，将其与神经网络和遗传算法等技术相结合，可探讨方法中的误差传播机理，以进一步研究方法对噪声敏感度及如何减少噪声对方法的影响，提高损伤定位指标的抗噪声干扰能力。

[1] STUBBS N， KIM J T.Field verification of a nondestructive damage localization and severity estinlation algorithm.texas a&m univ[R].reprort Prepared for New Mexico State Univ，1994.

[2] STUBBS N, KIM J T. Field verification of a nondestructive damage localization and sensitivity estimator algorithm[C]∥Proceedings of the 13JHJ International Modal Analysis Conference, 1995:210-218.

[3] STUBBS N,KIM J T. Improved damage identification method based on modal information[J]. Journal of Sound and Vibration,2002,252(2):223-238.

[4] HU S-LJ, LI H, WANG S. Cross-model cross-mode method for model updating[J].Mechanical Systems and Signal Processing, 2007,21:1690-1703.

[5] 曹 晖,林秀萍.结构损伤识别中噪声的模拟[J].振动与冲击,2010,29(5):106-109.

[6] 丁幼亮,李爱群,缪长青.大跨斜拉桥扁平钢箱梁损伤定位指标的噪声鲁棒性比较研究[J].公路交通科技,2007,24(4):79-83.

[7] BLACK C J, VENTURA C E. Blind test on damage detection of a steel frame structure[C]∥16th International Modal Analysis Conference (IMACXVI), California： Santa Barbara, 1998: 623-629.