基于BP神经网络的复杂布局管道泄漏检测研究

,, ,

(武汉理工大学 能源与动力工程学院，武汉 430063)

管流输送过程中，弯头数量越多，对泄漏的定位精度影响越大。这是因为流体在经过弯头处时，产生了能量损失和振荡，导致管道两端的压力传感器采集到的负压波信号的时间不够准确[1]。传统的直管道泄漏检测与定位方法不适用于复杂布局管道，有必要对复杂管道的泄漏检测与定位规律进行研究。

1 实验原理及方案

具有标准结构的BP神经网络，当隐层神经元数目足够多时，可以以任意精度逼近一个具有有限间断点的非线性函数[2]。因而只要选择合适的BP神经网络输入参数、训练目标和隐含层节点个数，就能对复杂布局管道泄漏进行检测与定位。

利用BP神经网络对复杂布局管道的泄漏检测与定位问题进行探讨。研究内容包括三部分：①泄漏状态辨识；②同一泄漏点不同泄漏量的泄漏检测；③同一泄漏量不同泄漏点的泄漏检测。

在实验台[3]中选择如图1所示的实验管道，最上面19 cm的管道是垂直输送的，管道末端为两个带90°弯头的普通弯管，中间一段是直管道。

图1 管道布局示意(单位：cm)

需要指出的是，在管道施工时，漏点1～3、漏点6～10都是直径3 mm的孔，漏点4作为电动调节阀是直径8 mm的孔，因而在实验中不能精确地调节直径3 mm孔泄漏量大小，漏点5是直径5 mm的孔。综合以上几个因素，第一部分的研究以漏点1～3、漏点6～9共7个泄漏孔的数据作为状态辨识依据，而第二部分的研究以漏点4电动调节阀作为对象，第三部分的研究以8个泄漏孔的数据作为依据。

2 神经网络各部分参数确定

2.1 输入层参数的确定

目前对于计算机的处理能力，如果直接将不经过任何处理的管道泄漏引发的压力采样信号都输入网络，则计算量会非常大，以致于不能收敛。因此，对于首、尾端的压力信号，选取信号使用db4小波进行3层分解后，将低频细节的平均值和高频细节的最大值作为BP神经网络的输入。

这样得到以一个近似的以“能量”作为输入特征向量的表征压力信号，据以判断管道的工作状态：

T=[A3首mean,D3首max,D2首max,D1首max,
A3尾mean,D3尾max，D2尾max，D1尾max]

(1)

当能量较大时，式(1)中的数值较大，不便于分析，应对特征向量进行归一化处理。

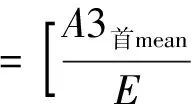
(2)

式中：E、E′——“能量”，

(3)

(4)

以某一波形为例，在Matlab中[4]，首先用wavedec函数对信号进行多步小波分解；然后用appcoef和detcoef函数来提取小波变换后的低频细节系数及高频细节系数；接着用wrcoef函数来重构第3层近似和各层细节；得到低频细节A3、高频细节D3、D2、D1。接着再用mean函数求出低频细节A3的平均值，用max函数求出高频细节D3、D2、D1的最大值。

2.2 训练目标的确定

1) 第一部分研究内容。由于是对管道泄漏状态进行辨识，信号包括漏点1～3，漏点6～9发生泄漏。共7个状态，所以神经网络的输出层使用3个神经元，由于3个神经元可以最多描述8个状态，因而训练目标确定为T=(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)，分别对应出现各种泄漏点时的工作状态。

2) 第二部分内容。当阀的开度从5%开始调到100%后，总共有20个状态，而且这20个状态也已经归一化，因而可以直接将其训练目标确定为T=(0.05,0.10,0.15,0.20,0.25,0.30,0.35,0.40,0.45,0.50,0.55,0.60,0.65,0.70,0.75,0.80,0.85,0.90,0.95,1.00)。

3) 第三部分内容。将各泄漏点距离首端传感器的距离作为训练目标。作为训练目标前，首先将其进行归一化处理[5]。需要说明的是，由于是研究复杂管道泄漏检测与定位规律，因而弯头也需进行处理，所有的距离都以实际距离为准，所有有弯头的地方都按照以往的结论进行处理，即弯头处的长度按1.6 m计算，各泄漏点距离首端传感器的距离及归一化后的结果见表1。

表1 各泄漏点距首端传感器距离及归一化结果

根据表1的归一化计算结果，第三部分研究内容的训练目标确定为T=[0,0.118 1,0.206 3,0.605 7,0.710 5,0.833 6,0.915 1,1.000 0]

2.3 隐层节点数的设计

多次试验发现，隐层节点数取输入节点数和输出节点数之间的值，在靠近输入节点时，网络的收敛速度较快[6]。但是也不能盲目地扩大节点数。因为节点数变大，虽然迭代次数变少，但网络明显变大，计算量变大，从而使计算时间变长。为此，提出一个单隐层隐层节点数的经验公式：

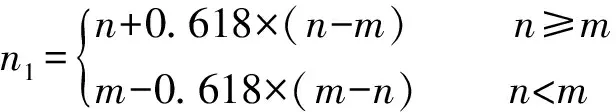
(5)

根据这种方法，得出第一部分研究内容的隐层节点数为11个，第二部分和第三部分研究内容的隐层节点数为12个。从而确定了BP神经网络的结构为8-11-3和8-12-1。

以第一部分研究内容为例，得到的网络结构见图2。

图2 神经网络结构

3 基于BP神经网络的泄漏检测

根据研究内容，对基于神经网络的复杂布局管道泄漏检测研究分为两部分：①基于BP神经网络的样本训练；②基于BP神经网络的预测。具体来说，在进行样本训练研究时，首先将所有的样本都作为神经网络的输入，以训练目标作为神经网络的目标；然后对每一个输入矢量在训练好的网络中进行计算；得到输出矢量，从而得到训练值。在进行预测研究时，输入样本比全部的样本少一个；对少一个的全部样本进行神经网络训练，得到训练好的网络；然后将这个样本放在训练好的网络中进行计算，从而得到预测值，将预测值与目标值进行对比，就可以得到预测误差。

3.1 基于BP网络的泄漏状态辨识

对复杂管道泄漏状态进行状态辨识时，以每个与泄漏孔对应的状态作为训练目标，对这7个孔发生泄漏后的输入矢量进行训练和预测，得到训练和预测输出见表2。

表2 泄漏状态辨识神经网络输出结果

由表2可见，对各个点泄漏后的输入矢量进行训练和预测后，实际输出值并不是简单的0和1。但是输出的结果已经很接近理想输出，其中训练输出的最大误差为0.064 8，而预测输出的最大误差为0.179 5，这是由于训练样本点过少造成的。虽然输出不是标准的0和1，但完全可以依靠程序判断管道工作模式，进而准确判断管道是否发生泄漏，进行泄漏状态辨识。

3.2 基于BP网络的泄漏量大小分析

对管道发生了不同泄漏量的泄漏检测进行研究时，以电动调节阀的调节开度作为研究对象，以泄漏量的大小作为网络的输出理想结果，对这20个状态泄漏发生后的输入矢量进行预测和训练，得到训练输出和预测输出见表3。

由表3可见，由于训练样本较多，BP神经网络非常逼近输入网络，在进行网络训练时，除了5%和10%泄漏量时训练误差较大以外，其余的泄漏量训练误差都在2%以内，这样的训练精度是比较满意的。由于网络训练比较好，因而在进行BP神经网络预测时，预测的效果也比较好，预测的最大误差为5.68%，最小误差为0.05%，这样的误差精度完全能满足实际工程的需要，能准确确定泄漏量大小。

3.3 基于BP网络的泄漏定位分析

以8个不同位置的泄漏点作为研究对象，泄漏位置见图1。以泄漏点的不同位置归一化后的结果作为网络的输出理想结果；对这8个点泄漏发生后的输入矢量进行预测和训练，得到训练输出和预测输出后，再进行反归一化处理；从而得到训练及预测输出的实际定位距离，结果及误差见表4。

表3 泄漏量研究神经网络输出及误差分析

表4 定位结果及定位误差

由表4可见，网络的训练误差非常小，这应该是因为选择了合适的隐层及合适的训练误差。但是网络的预测误差相对来说比较大，其中最大的定位误差达到了5.527 3%，但总的来说，定位精度大都控制在5%左右以内，这种定位误差应该可以接受。而且定位精度误差较大的一个根本原因就是训练样本太少，在一根接近7 m(直管管道长度)的管道上，只布局了8个泄漏孔来进行训练，只要定位误差在(8/7)/7×100%=16.326 5%以内，就可以认为误差没有超过不可接受的范围。提高精度的一个好的建议是多布置几个泄漏孔，增加训练样本库。

4 结论

1) BP神经网络的输入参数和训练目标必须明确，而且要能反映输入信号的特征，可以借助经验公式确定隐含层节点个数，但最好进行几个经验公式的对比，再来确定最适合的节点个数，另外所有的参数在进行处理前最好都进行归一化，以方便数据处理。

2) 用BP神经网络进行训练时，所有的误差都比较小，这也体现了BP神经网络强大的任意非线性逼近的能力。但用BP网络进行预测的时候，如果样本较少，则会产生较大的误差，样本数目足够多的时候，误差也会减小。

3) 对本实验台来说，用BP神经网络来预测复杂管道发生泄漏后的泄漏量大小是完全可行的；用其对是否发生泄漏进行状态辨识，则还要进行数据的二次处理；由于训练样本过少，用BP网络进行泄漏定位时产生较大的误差，建议多增加几个泄漏孔，也就是增加训练样本数，从而提高泄漏定位精度。

[1] 胡 琼.在役管线泄漏检测技术研究[D].武汉：武汉理工大学,2009.

[2] 葛哲学,孙志强.神经网络理论与Matlab 2007实现[M].北京:电子工业出版社,2008.

[3] HU Qiong, FAN Shi-dong. Development of pipeline leak detection system based on LabVIEW[C]∥2008 IEEE International Symposium on Knowledge Acquisition and Modeling Workshop Proceedings,2008, Wuhan, China,2008:671-674.

[4] 葛哲学,沙 威.小波分析理论与Matlab 2007实现[M].北京:电子工业出版社,2007.

[5] 晁智强,郭小牛,盛 锋.基于BP神经网络的某型两栖突击车风扇泵泄漏量预测研究[J].液压液气动,2009，(9):23-25.

[6] KUNG S Y. An algebraic projection analysis for optimal hidden units size and learning rates in back-propagation learning[C]∥International Conference on Neural Network, USA,1998:363-367.