基于均方差比归一化垂向梯度法的位场边界检测

王彦国，王祝文，张凤旭，张 瑾，邰振华，郭灿灿

(吉林大学地球探测科学与技术学院，吉林长春 130026)

基于均方差比归一化垂向梯度法的位场边界检测

王彦国，王祝文，张凤旭，张 瑾，邰振华，郭灿灿

(吉林大学地球探测科学与技术学院，吉林长春 130026)

针对位场数据处理中边界定位精度和识别能力的问题，提出一种新的边界检测方法——均方差比归一化垂向梯度法。均方差比(MSER)可进行边界识别，是针对边界点异常方向性和均方差衡量数据波动性提出的，对全区数据点4个方向的均方差进行归一化后选择各个数据点均方差比的最大值作为滤波输出实现的;均方差比归一化垂向梯度(NVD-MSER)可进行边界增强，是通过均方差比的垂向梯度及其总梯度的比值实现的。模型试验对比分析结果表明，NVD-MSER方法具有计算稳定性强、反映的边界位置连续性好、与实际模型边界对比偏差小的优点，这说明NVD-MSER法有较强的边界检测能力。用NVD-MSER法可以检测出黑龙江虎林盆地19条断裂，而欧拉反褶积只能识别出11条断裂，说明NVD-MSER法增强了对断裂平面位置的识别能力。

方位检测;边界检测;归一化;均方差比;梯度

边界检测是位场数据处理中解析地质构造、进行地质填图、圈定矿产范围等问题的重要方法［1-3］。大多数的检测方法是基于垂向或水平导数的极值点或零值点发展而来的［4-6］。目前常用的边界检测方法主要有水平总梯度法［7］及其改进方法［8-9］、归一化水平梯度法［10］、水平梯度归一化垂向导数法［11］以及导数归一化标准差法［12］。虽然这些方法均具有一定的边界检测能力，但存在检测不彻底或检测结果偏差较大的缺点。笔者在上述方法基础上，充分考虑边界点异常的方向信息，提出一种新的位场边界检测方法——均方差比归一化垂向梯度(NVDMSER)法，并利用该方法进行模型检验及实例分析。

1 方法原理

1.1 基本原理

如图1所示，将窗口(5×5)分解成以中心点为中心的4个子域，每个子域可以检测不同角度的异常变化(如图1中虚线所夹的角度)。首先计算出数据点4个方向的均方差，然后滑动到下一点，再计算出各个方向的均方差，直至完成全区内所有点的计算。由于全区不同方向均方差变化范围可能存在较大的差异性(例如全区x方向均方差变化幅度是y方向均方差的2倍(或2倍以上)，因此直接对每个数据点通过4个方向均方差进行检测时，y方向的边界或断裂可能未被检出，需对不同方向均方差进行归一化处理，使各个方向的均方差浮动均在同一范围内，然后利用各点不同方向的均方差比(归一化后的均方差)进行衡量，以均方差比最大值为滤波输出，最后对输出的均方差比进行导数换算，采用归一化垂向梯度进行边界增强处理。

图1 四方向子域剖分示意图Fig.1 Partition sketch map of four-directional subdomain

1.2 合理性分析

(1)全方位检测。每个子域可以检测出一定角度内的异常变化特征，4个方向便可以检测出中心点全方位异常的变化。

(2)归一化处理。由于全区不同方向的均方差变化不一，在进行滤波输出前对不同方向的均方差进行归一化是必要的。

(3)波动性分析。均方差是衡量一定大小窗口内数据局部变异性的一种有效手段。当数据比较平滑时，各个方向的均方差比均较小，同样输出的滤波值也较小;当数据变化较大时，各个方向的均方差比较大，通过全区内均方差比等值线极大值的圈闭形状及走向即可勾画出地质体的边界或断裂的位置，从而达到边界检测的目的。

1.3 计算步骤

(1)在每一个子域中分别计算出异常的均值Δfi及均方差 σi，即

式中，i代表4个方向中的某一方向;Ni和fi(j)分别为第i个子域的总计算点数和第i个子域第j个点的异常值。

(2)窗口滑动到下一点，计算出4个方向的均方差，依次进行，直至完成全部数据点。

(3)对均方差σi(x，y)进行归一化处理：

对全区σi(x，y)同时减去一个定数除了数值外，不改变其他特征。

对全区σ'i(x，y)同时除以一个定数除了数值外，同样不改变其他特征。在此，定义σ″i(x，y)为均方差比，则全区4个方向的均方差比变化均归一化到0～1之间。

(4)确定每个数据点4个方向中σ″i(x，y)最大值进行输出：

(5)计算均方差比的垂向梯度与总梯度的比值：

2 模型检验

采用6个不同参数的长方体叠加的复合模型进行检验，并分别利用水平总梯度、归一化水平梯度、水平梯度归一化垂向导数、导数归一化标准差以及本文提出的均方差比(MSER)及其归一化垂向梯度对模型体重力异常进行相应地检测处理。为了对比的统一性，在计算过程中所有方法均选择了相同的扩边模式，均未进行压制高频处理，均采用FFT法进行导数换算。

设x、y方向长度均为20 km，网格大小为0.1 km×0.1 km。组合模型体的各模型参数见图2，其中D1和D2分别是长方体的上顶和下底的深度(单位为千米)，6个长方体的剩余密度均为1.0 g/cm3。依据以上模型参数，利用长方体的重力异常计算公式，可获得复合模型在地面上所产生的重力异常(10－6m/s2)，结果见图 3。

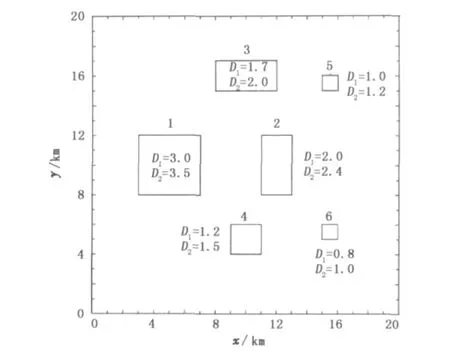
图2 复合模型体示意图Fig.2 Sketch map of superimposed models

图3 模型体产生的重力异常Fig.3 Gravity anomaly of model bodies

图4是不同边界检测方法识别出的边界位置结果(图中，黑色矩形框是模型体的理论边界;白色虚线是识别出的边界)。可以看出：水平总梯度法(图4(a))对边界有一定的识别能力，且检测出的边界位置与实际偏差不大，但识别模糊，检测不彻底，有相当一部分的边界无法有效识别;归一化水平梯度法(图4(b))和水平梯度归一化垂向导数法(图4(c))虽然可以较好地检测出边界的大致轮廓特征，但是检测出的边界位置均与实际偏差过大，严重影响了边界的定位精度;导数归一化标准差(图4(d))相对上述3种方法具有更强的边界识别能力，但仍有少部分边界无法识别，且存在着明显的边界效应;均方差比法(图4(e))检测出的边界偏差小，但同样未能较好地检测出所有模型体的边界;均方差比归一化垂向梯度法(图4(f))弥补了均方差比这一缺点，可以有效、清晰地检测出复合模型体的所有边界。

图4 不同方法边界识别结果Fig.4 Edge recognition results using different methods

以上分析结果表明，NVD-MSER相对其他方法具有边界检测能力强、检测边界偏差小、稳定性强的优点，同时可以同量级(即边界位置表现出极值大小相当)地检测不同深度不同规模的模型体边界。

3 实例应用

为了检验本文方法的实用性，选取了黑龙江省虎林盆地布格重力异常数据进行试验。虎林盆地位于那丹哈达岭燕山褶皱带和吉黑华力西褶皱带的交接处，是在构造复杂的环境中形成的中新生代坳陷带，其内部次级构造发育［13］，是大庆油田外围东带油气勘探的重点地区之一［14-17］。从原始布格异常等值线图(图5(a))可以看出，该地区重力异常等值线较为复杂，不仅有延伸较大的异常梯度带和大型重力高、低异常圈闭，也存在着异常等值线扭曲，次一级重力高、低异常的独立圈闭。MSER(图5(b))及NVD-MSER(图5(c))的极大值圈闭走向明显，均与原始异常等值线的梯度带或扭曲带位置相一致。图5(d)是利用MSER和NVD-MSER共同勾划出的19条断裂平面位置分布。可以看出，盆地内断裂主要以NE向和EW向为主(与重力异常表现出的断裂走向相同)。

为了进一步说明NVD-MSER方法划分断裂的准确性，采用Euler反褶积法［18-20］对虎林盆地布格重力异常进行断裂平面位置反演。从反演图(图6，其中“+”为反演的断裂点)可以看出：F1、F2、F3、F6、F7、F8、F17 这7 条断裂有清晰的显示;F4、F5、F9、F10 这4条断裂也有一定的显示;F11、F13、F15、F16、F18、F19仅有模糊的显示;F12、F14几乎无显示。NVDMSER法确定的这19条断裂在图5(c)中均有很清晰的显示，其中F1～F10断裂对应着重力异常的梯度带，F11～F19断裂则对应着重力异常扭曲带。

图5 边界检测实例检验及断裂分布Fig.5 Instance test and location of faults

以上对比分析结果表明，NVD-MSER法识别断裂有效，确定断裂位置准确，反映断裂走向连续，计算过程稳定，同时具有较高的分辨率。

对比分析图5，可以明显地看出F1～F7为虎林盆地的主干断裂，其中F2和F3是两条岩石圈断裂，是敦密断裂的两个分支［15-17］，F8、F9、F11、F12 同样在文献［17］中予以证实。对比重力异常的形态和Euler反演结果，可以说明本文方法划分出的其他平面断裂同样是合理的。

图6 Euler反褶积反演结果Fig.6 Inversed result using Euler deconvolution

4 结束语

本文中先对原始数据进行方位检测，再进行导数分析。模型检验和实例应用同时证实了该方法的正确性及优越性。本文方法原理简单、易于实现，且具有较快的计算速度和较强的稳定性，为位场数据边界位置的确定提供了一种新的思路。

［1］刘金兰，李庆春，赵斌.位场场源边界识别新技术及其在山西古构造带与断裂探测中的应用研究［J］.工程地质学报，2007，15(4)：569-574.

LIU Jin-lan，LI Qing-chun，ZHAO Bin.New detection techniques of geologic boundaries using potential-field data and its application in the Shanxi paleo-structure zone and faults［J］.Journal of Engineering Geology，2007，15(4)：569-574.

［2］钟清，孟小红，刘士毅.重力资料定位地质体边界问题的探讨［J］.物探化探计算技术，2007，29(增刊)：35-38.

ZHONG Qing，MENG Xiao-hong，LIU Shi-yi.A dicussion of boundary mapping by using gravity data［J］.Computing Techniques for Geophysical and Geochemical Exploration，2007，29(sup)：35-38.

［3］刘展，班丽，魏巍，等.济阳坳陷花沟地区火成岩重磁成像解释方法［J］.中国石油大学学报：自然科学版，2007，31(1)：30-34.

LIU Zhan，BAN Li，WEI Wei，et al.A method of inversing igneous rock by gravity and magnetic imaging in Huagou area of Jiyang depression［J］.Journal of China University of Petroleum(Edition of Natural Science)，2007，31(1)：30-34.

［4］ 罗孝宽，郭绍雍.应用地球物理教程［M］.北京：地质出版社，1991：139-154.

［5］ 李百祥.西秦岭地球物理场的地质解释［J］.甘肃地质学报，1997，6(2)：82-91.

LI Bai-xiang.Explanation of the geophysical field of the west Qinling［J］.Acta Geologica Gansu，1997，6(2)：82-91.

［6］WANG Wan-yin，ZHANG Gong-cheng，LIANG Jianshe.Spatial variation law of vertical derivative zero points for potential field data［J］.Applied Geophysics，2010，7(3)：197-209.

［7］ NABIGHIAN M N，GRAUCH V J S，HANSEN R O，et al.The historical development of the magnetic method in exploration［J］.Geophysics，2005，70(6)：33ND-61ND.

［8］HOOD P J，TESKEY D J.Aeromagnetic grad-iometer program of the geological survey of Canada［J］.Geophysics，1989，54(8)：1012-1022.

［9］WANG Wan-yin，PAN Yu，QIU Zhi-yun.A new edge recognition technology based on the normalized vertical derivative of the total horizontal derivative for potential field data［J］.Applied Geophysics，2009，6(3)：226-233.

［10］WIJNS C，PEREZ C，KOWALCZYK P.Theta map：edge detection in magnetic data［J］.Geophysics，2005，70(4)：39-43.

［11］COOPER，COWAN.Enhanceng potential field data using filters based on the local phase［J］.Computers and Geosciences，2006，32：1585-1591.

［12］COOPER G R J，COWAN D R.Edge enhancement of potential-field data using normalized statistics［J］.Geophysics，2008，73(3)：1-4.

［13］大庆油田石油地质志编写组.中国石油地质志：卷2，上册，大庆油田［M］.北京：石油工业出版社，1993：746-752.

［14］张凤旭，孟令顺，林泽付，等.黑龙江省虎林盆地重力异常、基底构造及油气远景区研究［J］.吉林大学学报：地球科学版，2004，34(4)：552-556.

ZHANG Feng-xu，MENG Ling-shun，LIN Ze-fu，et al.Study on gravity anomaly，basin structure and gas-oil potential of the Hulin Basin in Heilongjiang Province［J］.Journal of Jilin University(Earth Science Edition)，2004，34(4)：552-556.

［15］曹成润，刘正宏，王东坡.黑龙江省东部虎林盆地断块构造特征及其运动学规律［J］.长春科技大学学报，2001，31(4)：340-344.

CAO Cheng-run，LIU Zheng-hong，WANG Dong-po.The structure features and the movement regularity of fault blocks in Hulin Basin，eastern Heilongjiang Province［J］.Journal of Changchun University of Science and Technology，2001，31(4)：340-344.

［16］林泽付，薛进，杨恕，等.黑龙江省虎林市幅重磁场特征及其地质解释［J］.世界地质，2004，23(4)：397-401.

LIN Ze-fu，XUE Jin，YANG Shu，et al.Characteristics of gravity-magnetic anomaly and their geological interpretation on map-area of Hulin City in Heilongjiang Provinve［J］.Global Geology，2004，23(4)：397-401.

［17］张凤旭，张兴洲，张凤琴，等.黑龙江省虎林盆地单元结构的地质—地球物理研究［J］.吉林大学学报：地球科学版，2010，40(5)：1170-1176.

ZHANG Feng-xu，ZHANG Xing-zhou，ZHANG Fengqin，et al.Study on geology and geophysics on structural units of Hulin Basin in Heilongjiang Provinve［J］.Journal of Jilin University(Earth Science Edition)，2010，40(5)：1170-1176.

［18］THOMPSON D T.EULDPH：a new technique for making computerassisted depth estimates from magnetic data［J］.Geophysics，1982，47：31-37.

［19］REID A B，ALLSOP J M，GRANSER H，et al.Magnetic interpretation in three dimensions using Euler deconvolution［J］.Geophysics，1990，55：80-91.

［20］HANSIN R O，SUCIU L.Multiple-source Euler deconvolution［J］.Geophysics，2002，67：525-535.

Edge detection of potential field based on normalized vertical gradient of mean square error ratio

WANG Yan-guo，WANG Zhu-wen，ZHANG Feng-xu，ZHANG Jin，TAI Zhen-hua，GUO Can-can
(College of Geo-Exploration Science and Technology，Jilin University，Changchun 130026，China)

Aimed at the problems of edge positioning precision and recognition capability in potential-field data processing，a new edge detection technique based on the normalized vertical derivative of mean square error ratio(NVD-MSER)was presented.Mean square error ratio(MSER)can be used for edge recognition，and it is based on the directionality of boundary anomaly and the data volatility evaluated by mean square error.MSER can be achieved by the following steps：normalizing the four-directional standard deviation of the whole region，then selecting maximum from four directional MSERs of each and every data.NVD-MSER can be used for edge enhancement and it is the ratio of the vertical gradient of MSER and the total gradient.Comparative analyses of model test show that，the NVD-MSER has strong computing stability，good recognized edge continuity，and small deviation with model edge，so it has strong detection capability.In the application，NVD-MSER can detect 19 faults in Hulin Basin of Heilongjiang，while Euler deconvolution can identify 11 faults.It is shown that the NVDMSER method can enhance recognized stability in the planar location of faults.

azimuth detection;edge detection;normalization;mean square error ratio;gradient

P 312;P 631

A

10.3969/j.issn.1673-5005.2012.02.014

1673-5005(2012)02-0086-05

2011－08－27

国家自然科学重点基金项目(40739905);国家油气选区项目(14B09XQ1201)

王彦国(1985－)，男(汉族)，河南南阳人，博士研究生，主要从事固体地球物理学方面研究。

(编辑 修荣荣)