半潜式海洋平台的周期内波载荷分析

，，

(中国石油规划总院，北京 100080)

层化的海水在潮汐和地形的共同作用下形成了内波，这种现象广泛存在于海洋内部。随着人们海上生产活动的频繁化，不断发现有海洋结构物在内波经过时受到巨大的破坏。此外，海洋内波还严重威胁着船舶锚链系统和立管设施。因此，海洋结构物的内波载荷研究对于保证海上生产活动的顺利进行具有重要意义。目前，对海洋结构物内波载荷的研究主要是针对单根小直径桩柱[1-3]。以往的研究成果局限于一些简单构件，尚未结合复杂海洋结构物实际模型来解释内波经过时平台被推移的力学机制。

以代表海水密度强跃层分层的两层内波理论作为分析基础，结合某公司半潜式海洋平台结构参数和南海海洋环境条件参数建立了平台内波载荷计算模型，分析了周期内波作用的载荷特点，并讨论了波长、波高和密度跃层深度影响，最后将考虑相位差与不考虑相位差两种情况作对比。

1 平台周期内波载荷理论模型

1.1 两层分层的内波流场

尽管实际海水是连续分层的，但由于海水密度跃层位置及梯度千变万化，连续分层结构模型的应用将受到限制。本文采用代表海水密度分层强跃层的两层分层理论模型。设坐标原点位于海水表面，波传播方向为x轴正向，海水表面以上部分为z轴正向，海水上下层的密度分别为ρ1、ρ2，水深分别为d1、d2。引进上下层流体的流函数ψi(x,y,t)(i=1,2)，界面方程z=η(x)，则

(1)

(2)

上边界条件为

ψ1(x,0)=0

(3)

下边界条件为

ψ2(x,-d1-d2)=0

(4)

在自由界面z=η(x)上，运动学边界条件为

ψ2[x,-d1+η(x)]=-Q

(5)

式中：Q——某一恒定正常数, 表示稳态内波以下流体在(x,z)平面的体积变化量。

由于波面上的压强分布相等，结合Bernoulli方程可以得到

(6)

式中：R——正常数，与界面上的Bernoulli常数有关。

引入量纲一的量小参数ε=kH/2，k为波数；H为波高。

将流函数ψi(x,y,t)(i=1,2)和波面位移等按ε展开，流函数ψ1和ψ2可以表示为[4]

(7)

(8)

设上、下层流场的速度分量为(u1,w1)、(u2,w2)，则

(9)

(10)

由式(7)～ (10)可以确定各阶周期内波流场的水质点速度。

1.2 结构物内波载荷计算

由于海洋平台的结构尺寸与海洋内波波长的比值远小于0.15，故满足Morison公式的应用条件。定义内波流场速度向量VW为

VW=(uI,0,wi)

其中:i=1,2分别表示内波上下跃层。

记复杂结构物上一般位置构件轴线上的单位向量为e(ex,ey,ez)，其中ex、ey、ez可以用杆件在坐标系中的向量角表示。把内波流场任意水质点的速度矢量分解为垂直于和平行于杆件的两个分量，其中垂直分量记为UN，则UN=VW-(e·VW)e。一般位置杆件上单位长度上的波浪作用力可以表示为

(11)

假设对某一点O(x0,y0,z0)取力矩，杆件上任意一点的坐标为P(x,y,z)，则杆件单位长度上的波浪力对矩心的矩可以表示为

(12)

方程(11)中前半部分为阻力项FD：

(13)

方程(11)中后半部分为惯性力项FM：

(14)

式中：ρ——流体密度；

D——平台结构迎风方向上单位长度的面积，柱体结构截面形状影响CD与CM的取值，可参阅文献[5]。

由式(1)～(10)确定的内波流场及含平台结构参数的波载计算方程(11)～(14)即为本文计算平台周期内波载荷的理论模型。

2 平台分析模型及结果分析

2.1 平台分析模型

以某公司的半潜式平台为例，建立平台计算模型见图1。

图1 平台计算模型

平台体的几何特征简化由甲板、支柱和沉箱等结构组成，锚链一端与平台体连接、另一端设置为固定端约束。表1给出了平台结构基本参数，其所处的海洋环境条件见表2。内波流场为二维，平台为三维空间结构，波入射方向与平台浮体垂直，则平台上各构件波载可由式(11)～(14)积分求得。

海洋内波具有很强的随机性，常见波长可达数hm至数十km，不同波长的波周期及其诱导的内波流场也将发生变化；另外，波高和海水密度跃层位置也将直接影响两层分层的内波流场特性。下文将探讨平台在波长、波高或密度跃层位置发生改变时的周期内波载荷特点，最后将考虑相位差的影响。

表1 平台基本结构参数

表2 环境条件和内波参数

2.2 波长影响

图2是在波高(50 m)和密度跃层位置深度(100 m)保持不变而波长依次为600 m、1 000 m、1 500 m和2 500 m内波在一个波周期内的载荷。

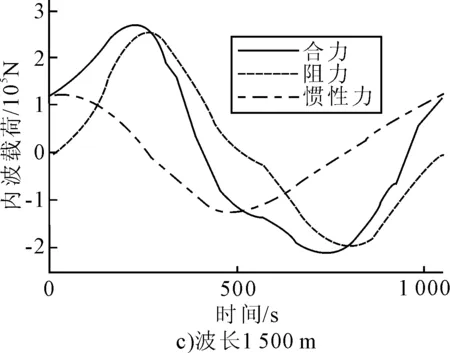
图2 波高(50 m)和跃层位置(100 m)均保持不变，平台在不同波长下的一个周期内的内波载荷

可以看出：随着波长增加，平台所受周期内波的最大载荷将相应增大；阻力值随波长增加而不断与合力值接近，另一分力惯性力值则越来越有偏差。说明对于波长较大的海洋周期内波，阻力项在合力中是主要分量，而惯性力却处于次要地位；当波长较小时，由于此时适用的周期内波理论为线性理论或低阶非线性理论，海洋平台受到的载荷在波传播方向上与反方向上的幅值相当，在这种情况下，平台会发生周期性震荡响应；当波长较大时，适用的波浪理论为非线性理论，平台所受的周期内波载荷呈现显著的非对称性，且沿波传播方向的内波载荷明显大于相反方向的载荷，此时对平台进行动力分析时，应根据内波理论适用范围选用合适的非线性内波理论。

2.3 波高影响

图3给出了波高20 m、60 m、90 m和120 m而波长(2 000 m)和密度跃层位置深度(300 m)保持不变的一个周期内的内波载荷计算结果。

可以看出：随着波高增大，周期内波载荷及其阻力项分力均产生较大变化，而惯性力分量的变化相对平缓；周期内波载荷的最大值、最大阻力项和最大惯性力项的变化趋势都随波高的增大而增大，且阻力值的最大增幅更为迅速；波高较小时，沿波传播方向上的周期内波载荷与相反方向的载荷幅值相当，但当波高较大时，前者明显大于后者，这类似于2.2中波长影响下的周期内波载荷变化特点。

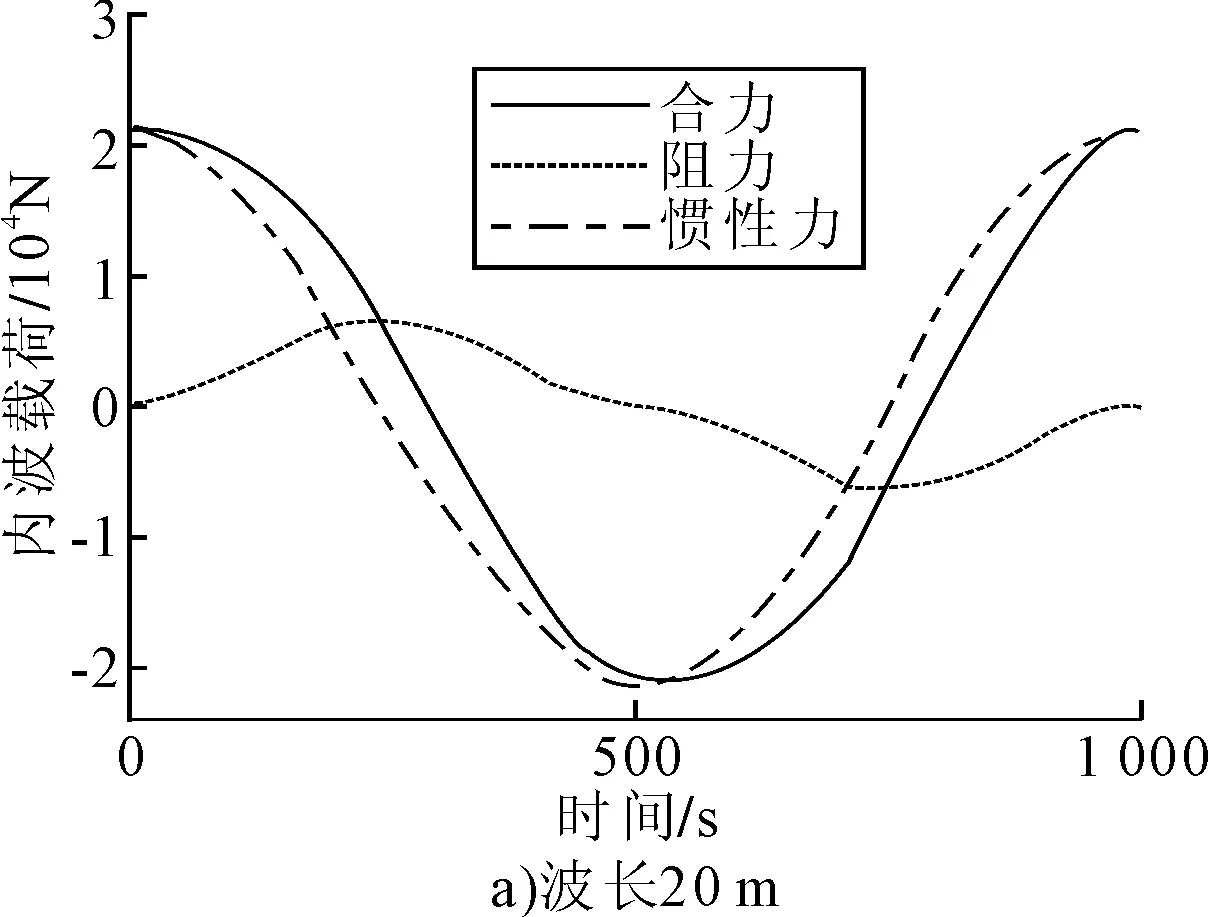
图3 波长(2 000 m)和跃层位置(300 m)保持不变，平台在不同波高下的一个周期内的内波载荷

2.4 密度跃层位置影响

海水密度跃层位置依次为100 m、300 m、500 m和1 000 m,波长(2 000 m)和波高(50 m)保持不变的一个周期内的内波载荷计算结果见图4。

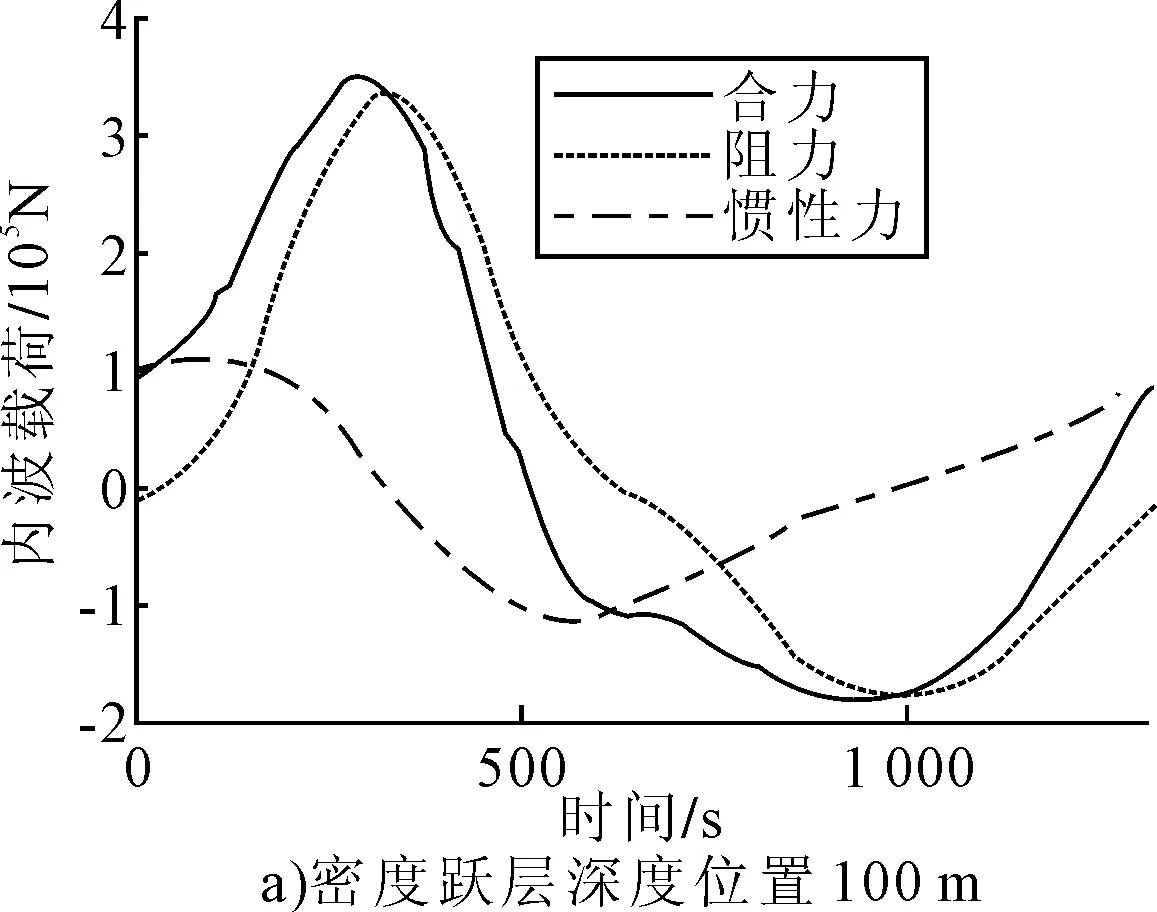
图4 波长(2 000 m)和波高(50 m)均保持不变，平台在不同密度跃层位置一个周期内的内波载荷

分析可知： 随着海水密度跃层位置的加深，阻力项分量急剧减小，平台所受的周期内波载荷幅值也不断减小；直至1 000 m深度时，“阻力”分力趋近于零，内波总载荷也几乎可以忽略。所以，对平台安全构成最大威胁的是密度跃层位置较接近水面的内波。

2.5 相位差影响

图5给出了“考虑相位差”与“未考虑相位差”两种情况下在一个周期内的周期内波载荷幅值，前缀NPD表示无相位差影响的计算结果，其中a)对应于波长600 m，b)为波长1 000 m的情形。

可以看出：对于波长600 m的周期内波，考虑相位差和未考虑相位差两种情况的计算结果差异很小；而当波长为1 000 m时，两种情况下的周期内波载荷、阻力项和惯性力项的变化曲线已基本重合。所以，当内波按照一定的入射角度作用于海洋平台时，相位差的影响可以忽略。

综上所述，表征内波流场特性的波长、波高和海水密度跃层参数的改变也将引起平台所受的周期内波载荷发生变化，而相位差的影响可以忽略；随着波长增加、波高增大或密度跃层位置靠近水面，“阻力”分力急剧变化，周期内波载荷的最大幅值将不断增大，该类内波的存在可能威胁到平台的安全。

由于分层流体造波比较困难，且要满足许多相似条件，本文的实验研究尚需造波技术的进一步发展。但周期内波特性可以通过所谓约化密度参数与表面波建立联系。

图5 平台在“考虑”和“未考虑”相位差两种情况下，一个周期内的周期内波载荷

3 结论

1)对海洋平台安全作业有威胁的周期内波是那些波长较长、振幅较大且密度跃层位置接近于水面的非线性周期内波。

2)当波长较短、波高较小且密度跃层位置较深时，适用的波浪理论为线性或低阶理论，周期内波载荷在一个周期内，两个方向上的波载荷幅值相当。

3)当波长较长、波高较大且密度跃层位置靠近水面时，在一个周期内，两个方向上内波载荷幅值呈现出显著的不对称性，沿波传播方向上的载荷明显大于相反方向载荷。

4)考虑相位差与未考虑相位差两种情况下的载荷特点基本相同，故相位差对周期内波载荷的影响可以忽略。

5)表征内波流场特性的波长、波高或海水密度跃层位置改变时，阻力分量发生变化明显，而惯性力项变化相对平缓。

[1] 叶春生,沈国光.海洋内波对小尺度圆柱体作用力的分析与计算[J].天津大学学报,2005,38(2)：102-108.

[2] 蔡树群,龙晓敏,甘子钧.孤立子内波对小直径圆柱形桩柱的作用力初探[J].水动力学研究与进展, 2002,17(4)：497-506.

[3] KASHIWAGI M. Wave-induced motions of a body floating in a 2-layer fluid[J]. International Journal of Offshore and Polar Engineering, 2005, 15(3)：175-182.

[4] YUAN Y T, LI J C, CHENG Y L. Validity ranges of interfacial wave theories in a two-layer fluid system[J]. Mechanica Sinica, 2007，23(6)：597-607.

[5] 李玉成，滕 斌.波浪对海上建筑物的作用[M].北京：海洋出版社，2002.