改进的差动算法在乙烯裂解炉支管温度控制中的应用

王宗宁， 李奇安， 李 悦， 单海欧

（辽宁石油化工大学信息与控制工程学院，辽宁抚顺113001）

裂解炉是乙烯生产装置的重要设备，对乙烯生产能力和装置平稳生产具有举足轻重的作用。裂解炉进料支管一般为4路或8路，由于燃料燃烧情况、炉膛温度分布不均匀、风量的变化等因素的影响，使得各支管进料不能得到均匀加热，从而导致裂解炉各支管出口温度不均衡。裂解炉各支管出口温度控制的优良，直接影响后续工序的操作稳定和乙烯收率。如果各支管温度偏差过大，温度低的物料不能完全裂解，温度高的物料则容易结焦，阻塞管内的物料流动，进一步加剧结焦现象，最终可能导致管壁烧穿而造成事故。因此支管出口温度均衡是裂解炉重要控制指标，对于节约能源，平稳生产，改善产品质量都具有重要的意义。

对于支路平衡控制问题，许多学者做了大量的研究并提出一些有效的解决方案。文献［1］利用一种两层递阶控制结构来克服各支路流量耦合特性。文献［2］把负载共享控制理论中的思想应用到多变量耦合的系统中。文献［3］运用等效系统的方法把一个对称的多输入多输出系统转化成两个等效的系统，再通过模糊控制方法对其进行控制。文献［4］提出了一种基于微粒群优化和模拟退火的约束广义预测控制算法，将微粒群优化和模拟退火引入到广义预测控制的滚动寻优过程中，增强对约束边界的搜索能力。文献［5］设计了先进控制系统并与DCS相结合实现了乙烯裂解炉温度控制。文献［6－7］提出一种基于差动法的控制算法，该方案把一个强耦合、多变量的控制问题转化成了几个常规控制问题，使问题得以简化。其缺陷表现在：基于差动法的四路均衡控制需要分别整定、设计三个平衡控制器，并且随着支路数的增加需要更多的平衡控制器，这在一定程度上增加了系统的不确定性和复杂性。

本文基于文献［8］提出了一种改进的差动平衡控制方案，通过把多个支路作为一个整体来处理，在总流量保持恒定的情况下，把一个多变量、强耦合的过程控制问题转化成了几个单回路控制问题，实现了支路的均衡控制，并进行了理论分析和仿真实验。

1 改进的差动算法原理

改进差动法的原理如图1所示，有N个支路，各支路的流量分别为f1，f2，…，fN，出口温度分别为T1，T2，…，TN，温度偏差分别为e1，e2，…，eN，出口温度平均值为¯T，流量偏差分别为Δf1，Δf2，…，ΔfN，各支路流量的初始值为fs1，fs2，…，fsN。

Fig.1 Principle diagram of improved difference method图1 改进差动法的原理图

由图1得知：

从（1）式和（5）式可得：

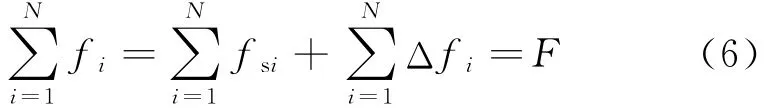
结论1： 如果N个支路的控制器是相同的，那么N个支路的流量偏差之和总是等于零。

证明：假设N个支路控制器都是比例－积分－微分结构。所有N个控制器都是相同的，即它们有相同的参数，即

其中，KP，KI和KD为比例系数、积分和微分增益，则N个支路流量偏差满足：

其中，E＝e1＋e2＋…＋eN，由（4）式知E＝0，因此（9）式的值为零，则N个支路流量偏差之和等于零，从而保证了总流量不变。

在这个控制系统中，每个支路都有一个控制器，输入是各支路出口温度与平均温度之差，输出是各支路流量偏差，通过这样的设计方案把N支路平衡控制问题转化成了N个单回路控制问题，这样给控制器设计带来了极大的方便。

2 控制器设计

改进的差动法控制系统方框图如图2所示，其中Gi（s）表示第i个支路的动态特性，Gi（s）是第i个支路控制器的拉氏变化，Di（s）代表了第i个支路的扰动，i＝1，2，…，N。¯T（s）和Ti（s）分别是¯T（t）和Ti（t）的拉氏变化，i＝1，2，…，N。从图2可知Ti（t）的拉氏变化满足（10）式。

Fig.2 Block diagram of improved difference control system图2 改进的差动法控制系统方框图

考虑Ti与¯T之差，i＝1，2，…，N，如果任意差值都趋于零，那么各支路出口温度都一样。由结论1可知，为了满足总流量不变的约束，所有的控制器Ci（s）都必须是一样的，用C（s）来表示。所以从（10）式可以得到，任意支路ei（t）＝Ti（t）－（t）的拉氏变化为：

根据终值定理，如果闭环系统是稳定的，即闭环特征方程的根都在复平面的左半平面。对于恒值干扰di（t），ei（t）＝Ti（t）－¯Ti（t）的极值是：

其中di是扰动di（t）的值，i＝1，2，…，N。

另外，根据控制系统原理可以知道，如果闭环系统是稳定的，对于恒值扰动，所有Ti（t），i＝1，2，…，N，都是有界的，因此（t）是有界的，即对任意给定的M＞0，总存在一个t0，对任意t＞t0，满足（t）的绝对值小于M，即：

就工业过程而言，常用的近似模型是一阶加纯滞后或二阶加纯滞后，对于这两种模型，它们的传递函数可统一表示为：

当Ti1或Ti2为零时，二阶模型就降低为一阶模型。当s趋于零时，这个传递函数的极限就是有限常数Ki。

由（12），（13）和（14）式可以得到，在闭环系统稳定的情况下，对于恒值扰动，如果控制器C（s）包含一个积分项K1／s，（12）式的值将为零。以上分析可以得到下面的结论：

结论2： 对于图2所示的系统，其各支路的出口温度都相同，必须满足以下条件：

（ⅰ）闭环系统稳定，即方程1＋C（s）Gi（s）＝0的所有根都在复平面的左半平面；

（ⅱ）所有控制器都相同，且控制器C（s）中至少包含一个积分项。

3 仿真研究

为了验证改进差动算法的可行性，进行了仿真实验，仿真模型采用某石化公司46万t／a的乙烯装置裂解炉（进料支管为8路）的进料流量与出口温度的近似动态模型。模型采用一阶惯性加纯滞后环节。即：

式中：Fi（s）为第i支路流量；Ti（s）为第i支路出口温度。仿真是在Matlab／Simulink仿真环境中运行的，控制器的设定值为各支管出口温度的平均值，即：

在整个支管温度平衡控制过程中应保证乙烯裂解炉进料总流量负荷的稳定，即：

系统运行至500s时投入控制器。从图3（a）中可以看到，系统在没有投入控制器之前出口最大温差达到20℃，在投入自动控制器大约经过25min后，各支路的出口温差将趋近于零。为了验证系统的抗干扰能力，当2 500s时在8个支路出口温度中分别加入不同大小的阶跃干扰，大约经过15min的时间，各支路出口温度趋于一致。经过控制器投入前后的比较可以看出，这种方案是可行的。

4 结束语

本文提出一种改进的差动支路平衡控制方案，这种方法通过把所有的支路看作是一个整体来处理，而在这个过程中进料总流量负荷不发生改变，从而把一个多变量、强耦合的过程控制问题转化成了几个单回路控制问题，使问题得到了大大的简化。尤其是当支路的数目很大时，也是很容易实现的，这种方案既包含了原有差动法的优点又克服了它的局限，仿真结果显示了有着较好的跟踪性能。

Fig.3 Simulation of pass temperature balance control图3 支路温度平衡控制仿真

［1］ 王金春，高衿畅，周春晖.高级控制策略在原油加热炉进料控制中的应用研究［J］.浙江大学学报，1995，29（2）：163－171.

［2］ Eitelberg E.Load sharing in a multivariable temperature control system［J］.Control engineering practice，1999，7（11）：1369－1377.

［3］ Abilov A，Zeybek Z，Tuzunalp O，et al.Fuzzy temperature control of industrial refineries furnaces through combined feedforward／feedback multivariable cascade systems［J］.Chemical engineering and processing，2002，41（1）：87－98.

［4］ 付秋峰.基于微粒群优化和模拟退火的约束广义预测控制算法［J］.石油化工高等学校学报，2010，23（2）：89－92.

［5］ 李平，李奇安，雷荣孝，等.乙烯裂解炉先进控制系统开发与应用［J］.化工学报，2011，62（8）：2216－2220.

［6］ 李嗣福，吴福明，陈红，等.炼油加热炉进料支管出口温度平衡控制［J］.信息与控制，1994，23（4）：243－246.

［7］ Wang Xing－xuan，Zheng Da－zhong.Difference control of parallel streams temperatures［J］.Journal of process control，2005，15（5）：531－536.

［8］ Wang Xing－xuan，Zheng Da－zhong.Generalized difference control of parallel streams temperatures［J］.Journal of process control，2006，16（5）：535－543.