浮置板轨道系统动力响应分析

耿传智 宫 寅

（同济大学铁道与城市轨道交通研究院，200331，上海∥第一作者，副教授）

城市轨道交通引起的振动噪声问题已受到广泛关注，世界各国相继研究开发了各种减振降噪技术。浮置板轨道结构作为一种特别有效的减振结构，在许多国家和地区已广泛使用，且在振动隔离、降低噪声方面取得很大成功。就其长度而言，施工现场浇注的浮置板单块可以长达数10 m，而工厂预制、现场安装的浮置板可以短至只有1 m多。在传统的浮置长板设计中，不同曲线地段的平纵断面要求是通过调整浮置长板的断面型式来实现的。但浮置板的断面、配筋等相关设计都较为复杂，无法进行通用设计，从而影响设计的工作效率。因此，国内外开始采用预制浮置短板、现场拼接的方法。目前，上海、北京、天津、南京等地使用的传统浮置长板结构的平面尺寸如图1所示，浮置短板结构的平面尺寸如图2、3、4所示，浮置板断面尺寸如图5所示。本文根据结构动力学原理，运用有限元分析软件Ansys建立浮置长板－隧道有限元模型、3种长度浮置短板－隧道有限元模型和普通轨道－隧道有限元模型，并运用落轴冲击法和施加实测轮轨力两种方法进行计算、分析和对比。所得结果可应用于工程实践，并可供浮置板轨道的选型和参数优化设计作参考。

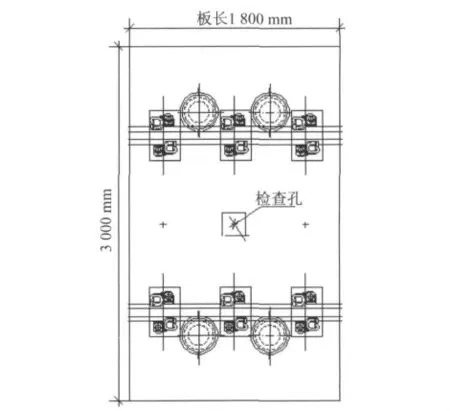
图2 浮置短板（1.8 m长）平面图

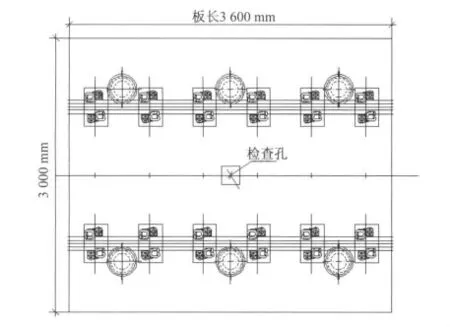
图3 浮置短板（3.6 m长）平面图

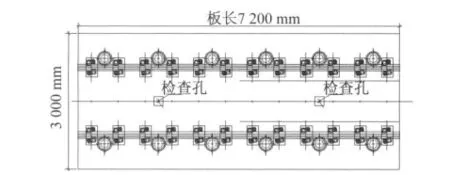
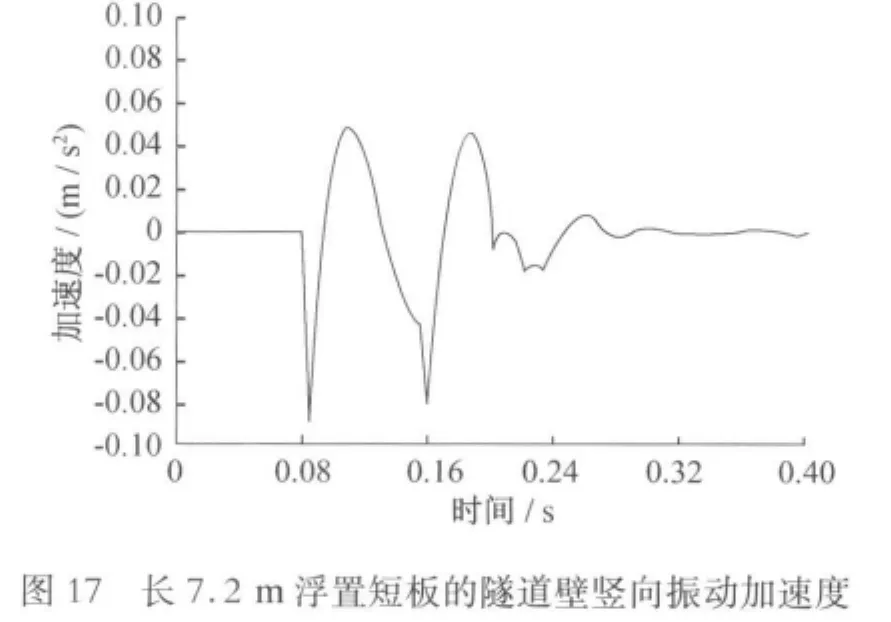
图4 浮置短板（7.2 m长）平面图

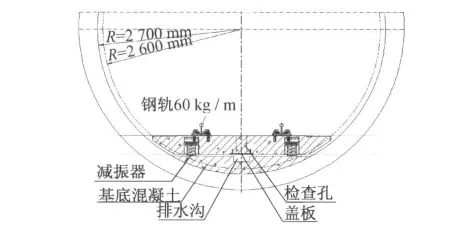
图5 浮置板断面图

1 浮置板落轴冲击动力性能有限元分析

当列车车轮通过不平顺的轨道时，车轮踏面可能与钢轨顶面脱离。由于车辆转向架的一系弹簧处于压缩状态，当车轮脱空时，压缩弹簧将轮对弹向轨面，造成轮轨冲击。基于该原理，用落轴方法可模拟列车运行时的轮轨间实际冲击［2］。

1.1 落轴冲击轮轨接触单元及有限元控制方程

由于车轮踏面为圆弧面，钢轨表面为平面，因此落轴冲击时轮轨间存在瞬时接触和分开的交错运动。此计算的重点和难点是如何建立合适的接触单元，准确模拟轮轨间强烈的瞬态非线性冲击。因此，需跟踪接触面上的点与目标面上的面（或线）的相对位置来确定两表面间的接触协调关系。现采用如图6所示的点面接触单元模拟轮轨接触。取踏面表面一节点M 以及钢轨表面一单元（节点编号为I，J，K，L）组成点面模型［2］，其中Q为轮轨接触点。若节点M侵入钢轨表面单元，形成一竖直于单元表面的接触力Fλ，M，作用在M 节点上，相应的反向力Fλ，η被分配到钢轨单元节点I、J、K、L 上。具体的有限元控制方程见文献［4］。

1.2 浮置板有限元分析模型及相关参数

传统的浮置长板的长度l＝25m，连续5块板，每块板下42个钢弹簧支座（如图1）；l＝1.8m的浮置短板，连续70块板，每块板下4个钢弹簧支座（如图2）；l＝3.6m的浮置短板，连续35块板，每块板下6个钢弹簧支座（如图3）；l＝7.2m的浮置短板，连续15块板，每块板下12个钢弹簧支座（如图4）；普通轨道长度取125m。钢轨采用CHN60轨，处理为梁单元；车轮采用块单元离散，轴重1.2t，根据总重不变原理将车轮处理为等厚度；轮轨间冲击采用Ansys软件中Contact点面接触单元模拟，仅考虑其轴向伸长与压缩，忽略弯扭剪切与扣件压力影响；扣件刚度取4×107N/m，阻尼取7.5×104N·s/m；钢弹簧的刚度取8.5×106N/m，阻尼取1×105N·s/m；浮置板混凝土强度等级为C30，以实体单元模拟。根据总体积不变原理将隧道简化处理为浮置板板下六面体模型，以实体单元模拟；隧道下均布土弹簧采用弹簧阻尼单元模拟；落轴冲击发生在相邻两扣件间钢轨中线位置，落轴高度取25mm［4－5］。浮置板－隧道有限元模型如图7所示，普通轨道－隧道有限元模型如图8所示，浮置板有限元模拟局部放大见图9所示。

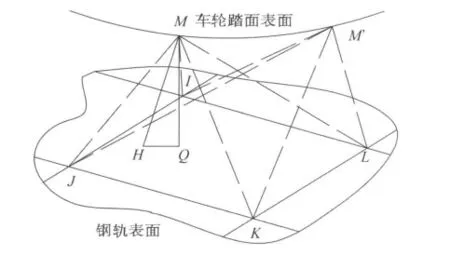
图6 轮轨点面接触单元

2 浮置板落轴冲击动态响应结果比较

现对不同长度规格的浮置板落轴冲击动态响应结果比较如下。

2.1 浮置板竖向振动加速度的比较

在计算结果中提取落轴位置下方浮置板轨道的竖向加速度，分别在时域内和频域内对浮置板的竖向加速度进行比较。

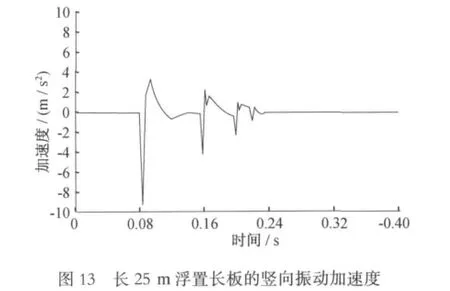
时域内对浮置板竖向加速度的比较见图10～13所示。

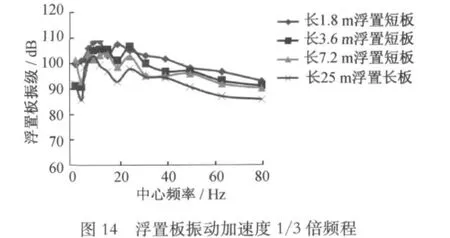
将各模型计算结果的浮置板竖向振动加速度时程曲线进行离散傅里叶变换，得到频域内对应于各频率的加速度幅值，再进行1/3倍频程变换，按规范进行记权。结果如图14所示。

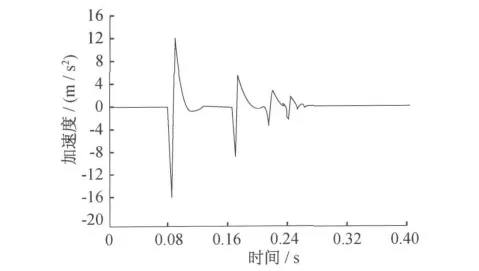
图10 长1.8m浮置短板的竖向振动加速度

由图14可知：随着浮置板长度的增加，浮置板竖向振动加速度幅值减小，但减小幅度较小。

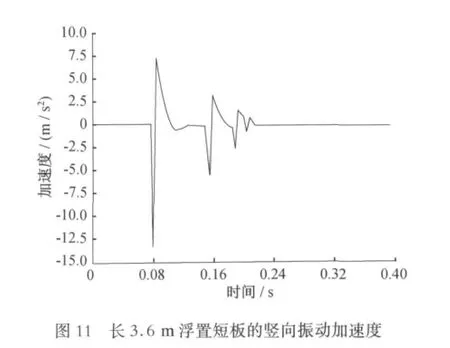
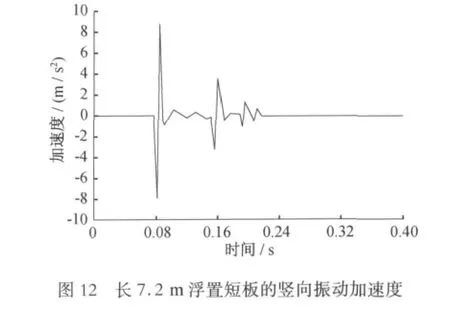
2.2 隧道壁竖向振动加速度的比较

分别在时域内和频域内对隧道壁的竖向振动加速度进行分析比较。

时域内对隧道壁的竖向加速度分析比较见图15～19。

将各模型计算结果的隧道壁竖向振动加速度的时程曲线进行离散傅里叶变换，得到频域内对应于各频率的加速度幅值，再进行1/3倍频程变换，按规范进行记权。结果如图20所示。

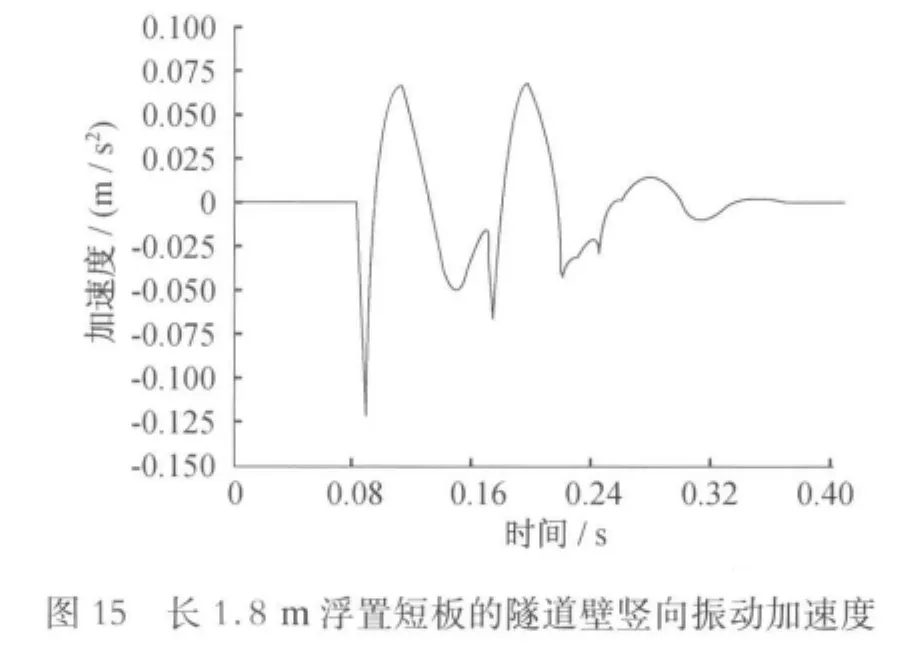
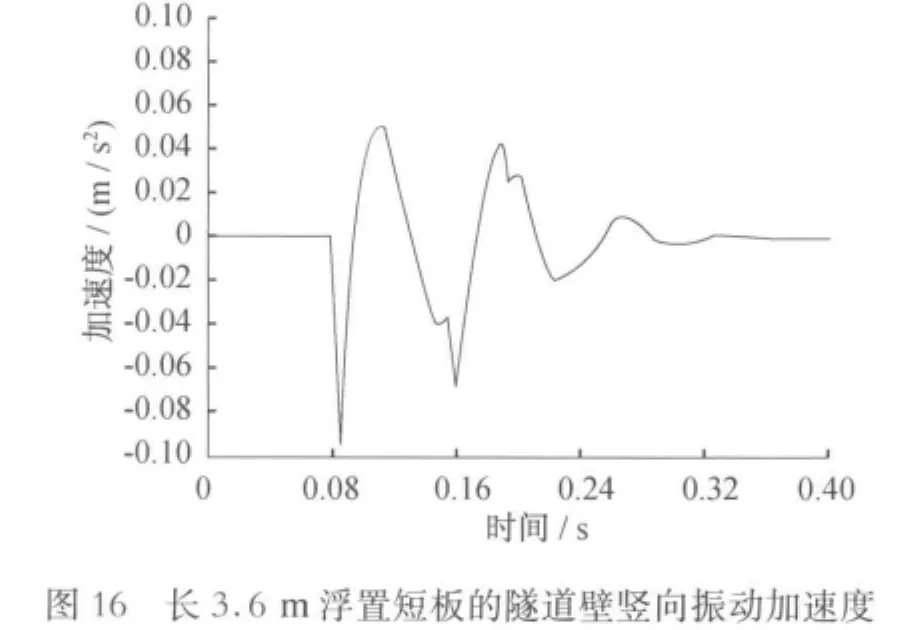
由图20可知：浮置板轨道在20～80Hz内具有良好的隔振效果，可减少振动6～25dB。

3 浮置板在实测轮轨力作用下的动力响应分析

3.1 浮置板分析模型建立与实测轮轨力的施加

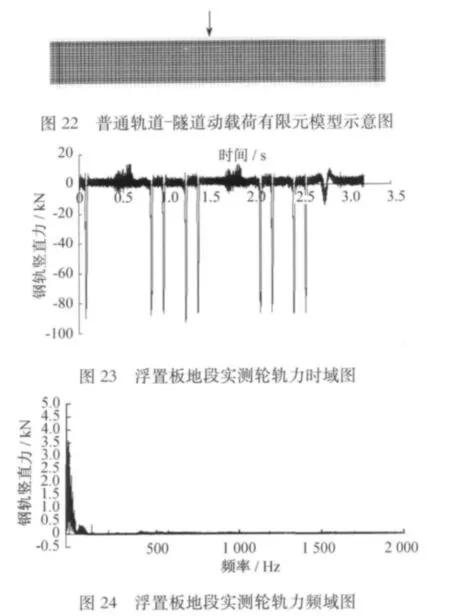
浮置板模型参数同上述有限元分析的落轴冲击模型参数。浮置板－隧道动载荷有限元分析模型如图21，普通轨道－隧道动载荷有限元分析模型如图22。将实测轮轨力分别施加在各模型，进行谐响应分析。实测轮轨力时域见图23，频域见图24。

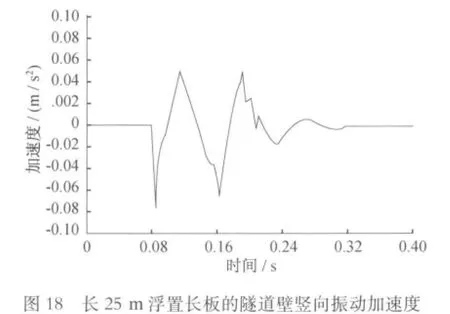
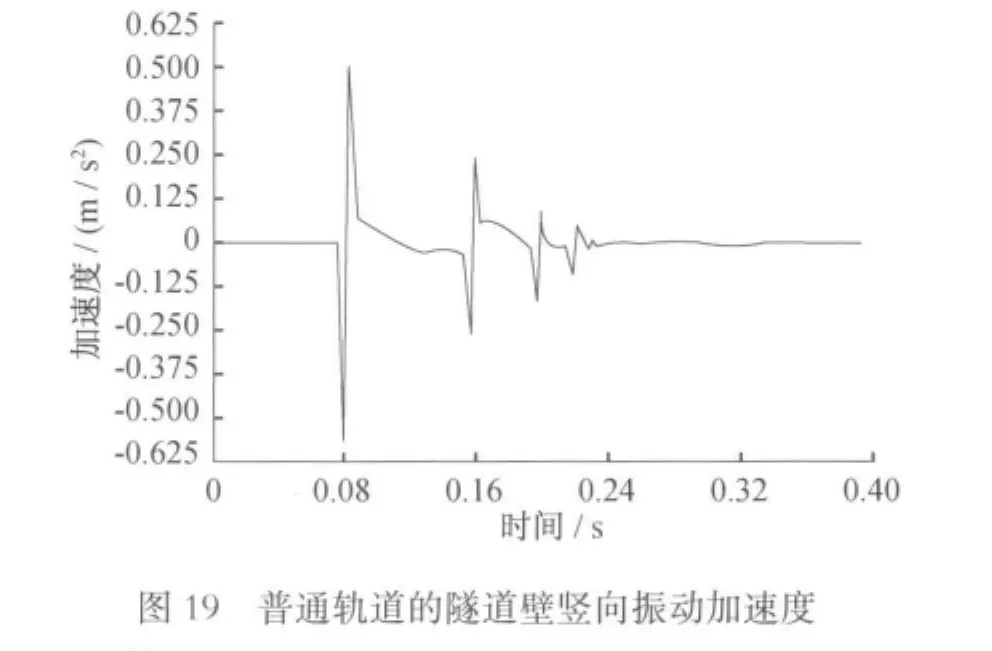
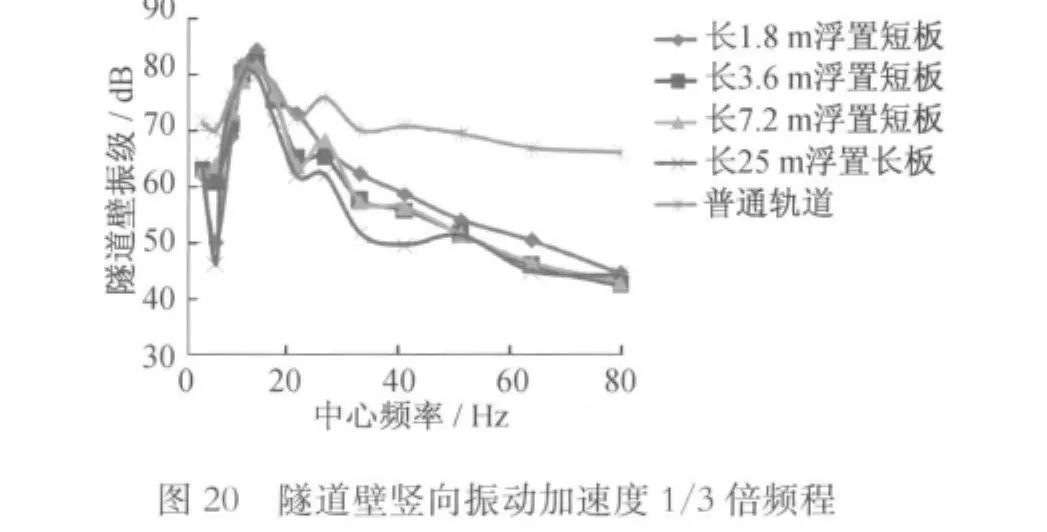
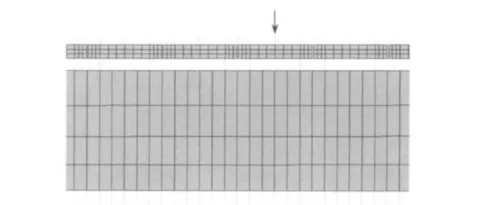
图21 浮置板－隧道动载荷有限元模型示意图

3.2 浮置板施加实测轮轨力计算结果分析

对不同长度规格的浮置板施加实测轮轨力的动力响应结果比较如下。

3.2.1 浮置板竖向振动加速度的比较

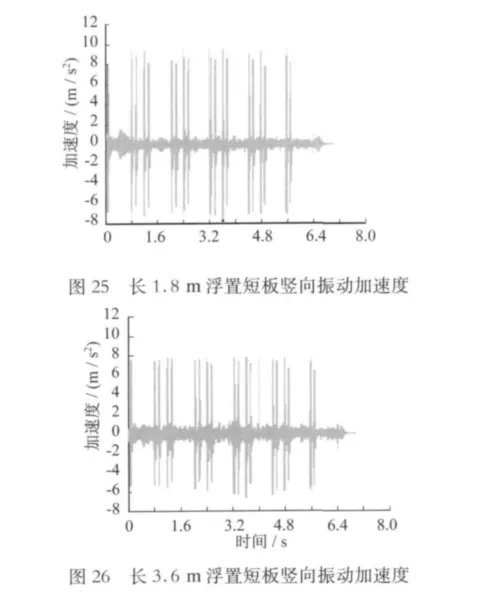
对时域内浮置板的竖向振动加速度比较见图25～28所示。

将各模型计算结果的浮置板竖向振动加速度时程曲线进行离散傅里叶变换，得到频域内对应于各频率的加速度幅值，再进行1/3倍频程变换，按规范进行记权。结果如图29所示。

由图29可知：随着浮置板长度的增加，浮置板竖向振动加速度幅值减小，但减小幅度较小。

3.2.2 隧道壁竖向振动加速度的比较

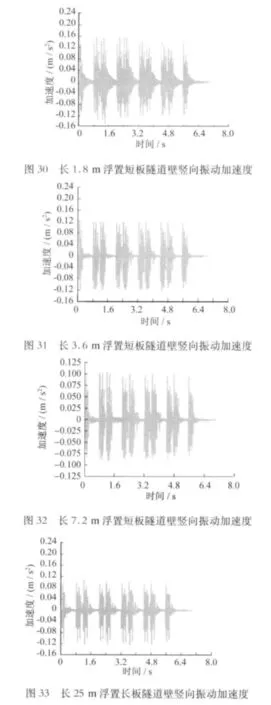
对时域内隧道壁竖向振动加速度的比较见图30～34所示。

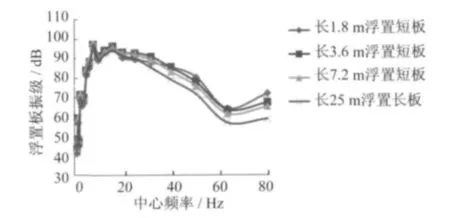
图29 浮置板竖向振动加速度1/3倍频程

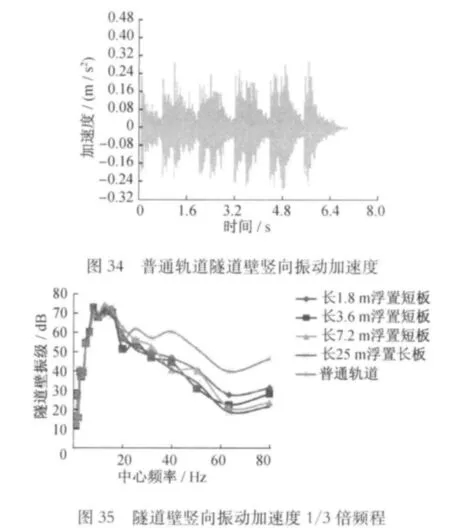
将各模型计算结果的隧道壁竖向振动加速度的时程曲线进行离散傅里叶变换，得到频域内对应于各频率的加速度幅值，再进行1/3倍频程变换，按规范进行记权。结果见图35所示。

由图35分析可知，浮置板轨道在20～80Hz内具有良好的隔振效果，可减少振动6～25dB。

4 结语

对应于现场浇注和预制的浮置板，分别建立浮置长板轨道－隧道、浮置短板轨道－隧道和普通轨道－隧道有限元模型，分析了浮置短板、浮置长板和普通轨道在落轴冲击作用下和实测轮轨力作用下的动力响应性能，通过分析，两种方法获得了一致结论：浮置板轨道在20～80Hz内具有良好的隔振效果，可减少振动6～25dB。浮置板轨道隔振性能主要由其固有频率决定，并不是由长度决定，只要浮置短板和浮置长板的固有频率相同，隔振性能基本相同。本文结果可供浮置板轨道的选型和参数优化设计作参考。

［1］王炯，吴天行.浮置板轨道隔振性能研究［J］.上海交通大学学报，2007，41（6）：1022.

［2］练松良.轨道动力学［M］.上海：同济大学出版社，2003.

［3］Wrigges P，Simo J C，Taylor R L.Penalty and augmented lagrangian formulations for contact problems［C］∥Proceedings of the NUMETA.Swansea：British Technique Press，1985.

［4］朱剑月，耿传智.高架弹性支撑块轨道结构落轴冲击动态响应［J］.同济大学学报：自然科学版，2005，33（12）：1621.

［5］耿传智，王伟鹏.地铁弹性扣件减振性能的落轴冲击仿真分析［J］.振动与冲击，2010，29（3）：113.

［6］赵录怀.信号与系统分析［M］.北京：高等教育出版社，2003.

［7］耿传智.地铁系统振动控制研究［D］.上海：同济大学土木工程学院结构工程与防灾研究所，2006.

［8］朱志强.地铁钢弹簧浮置板道床存在的缺陷及设计优化［J］.城市轨道交通研究，2010（7）：50.