创设物理情境，改善数学教学效果

谢歆鑫

(西安航空职业技术学院，陕西西安710089)

创设物理情境，改善数学教学效果

谢歆鑫

(西安航空职业技术学院，陕西西安710089)

针对高职院校高等数学教学效果不佳的现状，以及数学与物理在发展过程中互相影响、互相促进的独特关系，通过实践教学案例发现，合理运用物理情境辅助数学教学，可以使得数学教学具体、生动和形象，进而达到启发学生实际应用和培养学生综合素质的教学目的。

物理情境;数学教学;案例;教学效果

一、问题的提出

高等专科数学是高职理工科学生必修的一门功课，也是理工科学生将来学习专业课的一门很重要的工具，然而学生的学习积极性却不高。尽管知识深度一再变浅，但是效果仍不尽如人意，于是师生双双陷入痛苦之中。如果说这种现象是一种“病态”，其实病根很容易找到，就是学生对数学不感兴趣。但凡人对某种事物没有了兴趣，就失去了主动去钻研的动力。为什么会造成这种结果呢?原因是复杂、多方面的，比如教育制度的缺陷。从中小学开始，数学教学就在高考的指挥棒下变得愈发急功近利，陷入应试教育的僵化模式而不可自拔：只重视传授现成知识、培养逻辑推演和计算能力，并且形式化、抽象化，处处只见定义、定理，却看不到数学理论形成和发展的过程以及其中所蕴含的精妙的思想方法，更谈不上运用数学思想和方法去分析解决问题。长此以往，学生关于数学的认知结构完全是由公式、定理堆砌而成，由此造成学生主动学习的动力逐渐丧失殆尽。

事实上，数学是研究现实世界的空间形式和数量关系的学科，它来源于客观世界，因此必定与现实世界的各种事物有着千丝万缕的联系。数学离不开具体的问题，否则数学就成了空洞的理论，它的成长需要实践的土壤和多学科的共同协作。这种实际问题的背景恰恰是数学的源泉，是它们让数学变得生动，富有挑战性和创造性。放眼世界，现代数学已经成为发展现代科技的动力。作为教学的实践者，我们需要对当前的数学教学进行思考，而思考的出发点就应当是如何把数学教学与实际问题情境结合起来。比如说，可否将相应的数学内容与我们身边的物理现象结合起来，使我们的数学教学可以在对这些物理问题的思考、分析和解决过程中得以展开和完成?我们先从数学与物理的历史渊源谈起。

二、数学与物理的历史渊源

回顾历史，数学理论几乎全部是在人们试图理解物理规律的探索中诞生出来的，同时，数学又为物理提供了描述规律的语言。在此，不得不提到数学发展史上的两个典型事件。

第一个事件的主角是伽利略，著名的物理学家。他为物理学写下了真正的首页，为什么这样说?原因是在他之前，世界范围内的物理研究活动只停留在对自然现象的观察、记录和总结。自伽利略开始发生了转变，他认为自然界是用数学设计的，宇宙是一部巨著，其中的内容是自然哲学，它的语言是数学语言，只有掌握了数学这个工具才能读懂它。伽利略是物理学数学化的伟大实践者，他开创了科学实验与数学相结合的新领域——实验数学。依靠数学推理，伽利略断定，亚里士多德关于“不同重量物体下落时间也不同”的结论是错误的。这种动用数学工具对自然现象量的变化进行分析，细致而深刻地探索其内在规律的研究活动，就是科学数学化的主要特征。

第二个事件的主角是牛顿和莱布尼兹，他们创建了微积分，数学和物理由此都走进了新纪元。微积分的创建让过去系列初等数学无法解决的问题纷纷迎刃而解并取得巨大突破，同时也催生了新的数学理论的产生，比如变分法为牛顿力学奠定基础，偏微分方程阐述了麦克思韦电磁理论等等。

纵观数学和物理的发展历史，可以清晰地看到两者始终是相互交织相互促进。物理学家详细地研究某些自然实例，数学家则提出普遍而有深远意义的理论。数学理论为物理学研究提供工具而使物理学得以发展;同时，物理学的进步以及数学自身矛盾运动的结果，又刺激了数学向更为深广的领域拓展。数学与物理学就是这样互相依赖、不可分割。

三、创设物理情境进行数学教学

学生对身边事物是最感兴趣的，让学生在实际、生动的情境中展开学习是完全可行的一种教学策略。从上面可以看到数学和物理有着深厚的渊源，我们完全可以运用物理情境负载相关数学主题完成数学教学任务。在此，我们辅以几个教学案例。

【案例1】联系生活，知识兴趣化

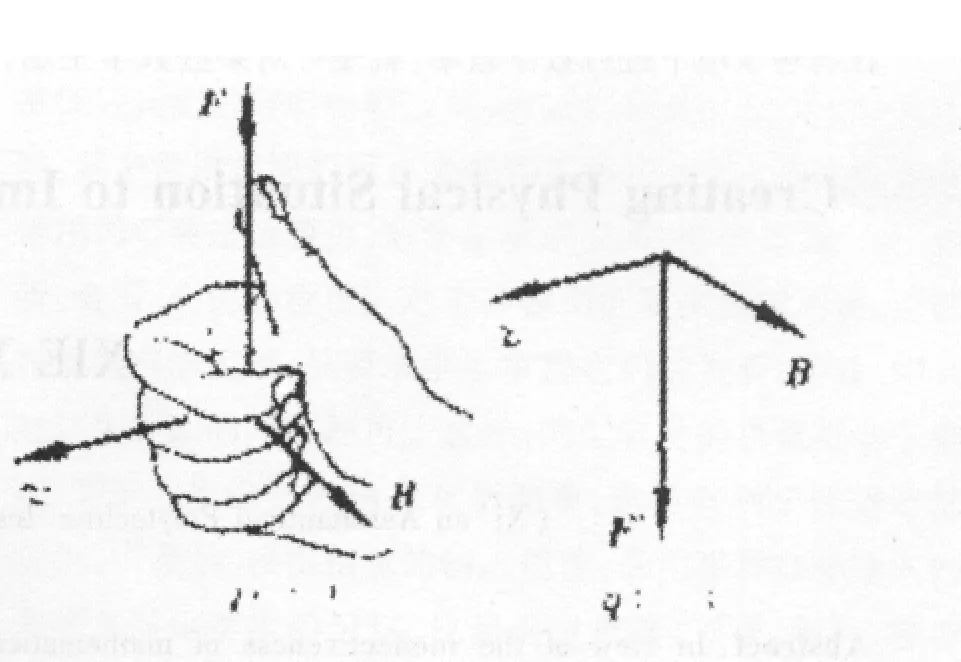
图2 右手螺旋定则

讲授定积分物理应用：求转动惯量I。这是一个学生以前没有接触过的刚体力学中的概念，学生将来在工程技术中会经常用到，因此有必要阐述清楚，而且有助于使用数学解决问题。但面临的实际情况是，刚体力学知识对学生而言是空白，在有限课堂时间内不可能讲得系统。拟采用类比和实例来讲清这个概念。首先，把刚体力学中转动惯量同质点运动学中的质量进行联系对比，获知其计算公式I=为了进一步加深对概念的理解，接着引出自然界的三大守恒定律之一——角动量守恒定律，得到守恒定律公式I2ω2=I1ω1。理论上虽然完成了，但效果还远远不够，能感觉到学生仍感枯涩。重要的是第二步，播放花样滑冰视频、跳水视频，让学生观察它们的运动特点，进而总结两者的共同点。然后与守恒定律公式联系起来，发现这两个运动在旋转转动动作中，都需要改变转动速度;而要改变转动角速度ω，就必须改变人体转动惯量I，转动惯量的改变需要不时地调整人体转动的半径和质量分布。这正是我们所要解决的问题，即定积分求解转动惯量。

【案例2】突破教材，概念简单化

讲授向量代数部分。概念 ——两向量的向量积(叉积)：C=A×B。客观地说，对于学生，从数学角度来看这是个没有任何意义的公式，难以接受这个概念。这部分教学内容在众多的教材安排中，通常选择两种方式引入：一种是直接给出，另一种是借助物理上“力矩”概念引入。从以往教学效果来看都不理想。原因是第一种方式没法理解和消化概念，第二种方式强调“力矩”是矢量概念太陌生(高中物理没有也无须指出)。所以，需要突破教材，另辟蹊径，寻找其它学生所熟悉的物理情境。于是，我们联想到高中时期学生最熟悉的物理概念：洛伦兹力——运动电荷在磁场中受到的磁场力(图1)，Fm=q·ν×B，其中，力的大小为：Fm=qνBsinθ;力的方向判断：右手螺旋定则。

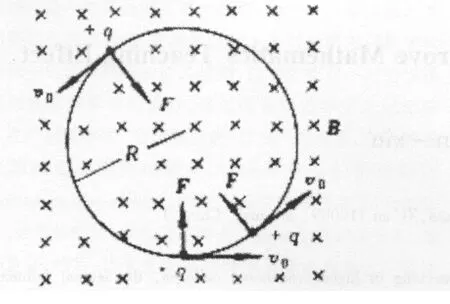
图1 运动电荷在磁场中受力图

这样可以为学生顺利地引入向量积的概念;同时，强调两个向量的向量积大小和方向与洛伦兹力判定完全相同。其中需要指出的是右手螺旋定则和高中时的左手定则效果一样，且更方便、形象，因为右手螺旋定则如同我们生活中用螺丝刀拧螺丝钉一样生动(图2)。

【案例3】紧跟时事，问题热点化

根据实际问题列解微分方程，这在讲解微分方程时是一个难点。需要根据实际问题背景，找出主要因素，构建正确的关系方程，并能求解列出的方程。

实例：求放射性元素的衰变规律问题。这个问题会令学生感觉有些遥远且显得高深。为了缩短这种距离感，我们跟踪时值发生的事件，即2011年3月11日日本本州东海岸附近海域发生里氏9.0级地震并引发海啸，造成福岛核电站严重核泄漏，泄漏的主要放射性物质是碘-131。由此把问题的研究对象由原来的铀-235换成了碘-131。这样做既不会改变教学的初衷，同时又引起学生的关注，使得他们有兴趣去解决这个问题。

当然，在完成这个问题过程中，可以适时补充一些相关知识，如碘-131，原子核内质子数是53个，中子却有78个，质子、中子总数是131个。中子数较稳定态多了4个，自然就处于不稳定状态，遇到原子核能级变化或其他触发条件，中子就会从原子核内散逸出去，同时释放出一定能量的射线，所以具有放射性，其半衰期为8.02天。该物质通过大气传输，溶于水，浓度超标会导致甲状腺癌。3月15日早北风吹到距离福岛220公里外的东京，东京浓度突增20倍，但辐射量仅相当于旧式电脑显示器的辐射量，东京市民没有恐慌，中国距离日本数千公里，有必要恐慌吗?甚至发生“抢盐”的一幕。数据显示，3月30日，陕西也检测出碘-131，但仅为天然本底辐射剂量的十万分之一，相当于乘坐飞机飞行2000公里所接受宇宙射线辐射的千分之一，因此我们更不必恐慌。要培养独立思考的习惯，谣言止于智者。

以上这些切实的教学案例体现了我们的初衷，是希望给单纯的数学问题尽量赋予一定的实际背景，以引起学生的兴趣，调动学生探求知识的积极性、主动性，达到教学的目的。从效果来看，学生是乐于接受的，达到了教者轻松、学者容易的双赢效果。

结语

在物理情境下进行数学教学，就是针对某些数学主题，选取适当的物理原型，创设物理情境，借助物理原型的形象直观性，在感性认识的基础上，通过对一系列物理问题的分析，建立相应的数学模型，寻找解决问题的数学方法，建立相应的数学理论，以便解决具有同一类数学结构的现实问题。这一过程，力求使学生在实践性的工作中将“感知经验”、“数学逻辑”、“问题方法”紧密结合起来，并在实践过程中探索、掌握和运用知识，培养思维能力，建立数学观念和意识。

很显然，采用这种教学方法，对教师的知识素养提出了更高要求，这不仅指教师已有的知识素养，还包括教师能够不断通过自我更新补充新知识的能力，以及从诸多相关学科中汲取自己学科所需教学素材的敏感性，因为数学的发展不仅与物理还与其它诸多学科是密切相关的。

［1］王晶昕.数学主题情境教学［J］.数学教育学报，2001，(2)：7-9.

［2］李心灿.微积分的创立及其先驱［M］.北京：航空工业出版社，1991.78-86.

［3］阎金铎.物理教学论［M］.南宁：广西教育出版社，1996.

［4］欧维义.数学物理方程［M］.长春：吉林大学出版社，1991.

［5］潘忠诚.数学物理方法教程［M］.天津：南开大学出版社，1993.

Creating Physical Situation to Improve Mathematics Teaching Effect

XIE Xin-xin
(Xi’an Aeronautical Polytechnic Institute，Xi’an 710089，Shaanxi，China)

In view of the ineffectiveness of mathematics teaching in higher vocational colleges，the mutual influence of mathematics and physics on each other in the development process，and the relationship between mathematics and physics，this paper studies and discovers that a reasonable use of physics case can help mathematics teaching，and make it concrete，vivid and visual，then reach the teaching goal of inspiring students＇application and cultivating their comprehensive quality.

physics situation;mathematics teaching;case;teaching effect

O13-4

A

1008-8156(2012)01-0076-03

2012-02-27

2012-03-08

谢歆鑫(1979-)，男，陕西安康人，西安航空职业技术学院讲师。研究方向：功率超声及换能器设计。

本文系陕西省职教学会教育科研项目(SZJYB2011014)的研究成果。