基于遗传灰色GM（1，1，ρ）模型的短时交通流量预测

吴宝春，郑蕊蕊，李 敏，杨亚宁

（大连民族学院 信息与通信工程学院，辽宁 大连116600）

短时交通流量预测是智能交通系统的一个研究热点，实时并准确的短时交通流量预测是实现交通控制和诱导的前提和技术基础，是影响智能交通系统可靠性的关键技术。短时交通流量预测是指利用预测算法分析已有的交通流量数据，对未来某段时间内的交通流量做出预测，以便及时采取适当的交通控制和诱导措施，达到方便出行、缓解道路拥堵、节能减排等目的[1－2]。由于交通控制的最大周期是2.5～3 min，交通诱导的周期一般是5 min，因此，短时交通流量预测一般指预测5～15 min之内的交通流量。

目前对短时交通流量的预测主要采用的方法可分为两类：即基于传统统计理论的方法和智能信息处理的方法[3]。由于道路交通系统是由人为参与、时变的复杂非线性系统，具有高度的不确定性，受随机干扰影响大，规律性不明显，随着预测周期的缩小，这种随机性、不确定性和非线性愈强。因此，传统的统计理论模型在预测精度和实时性方面难以达到要求[4]。神经网络等智能信息处理方法不需要严格的数学推导和明确的物理意义，对非线性和不确定性问题具有很强的适应性，在短时交通流量预测中取得了显著的成效[5]。但是神经网络需要大量的数据进行训练，模型的结构参数等对预测结果的影响较大且依赖于人的经验。灰色模型是灰色理论[6]的预测模型，具有所需样本小、预测准确度高、运算量小等特点，非常适合于短期预测，已成为短时预测的主要方法。文中利用遗传算法根据已知数据优化灰色新陈代谢GM（1，1，ρ）模型的背景值参数 ρ，采用遗传灰色 GM（1，1，ρ）模型对实时采集的交通流量数据进行仿真分析，实验结果验证了该模型的准确性、实时性和有效性。

1 遗传灰色 GM（1，1，ρ）模型

1.1 灰色 GM（1，1，ρ）模型

灰色模型（Gray Model，GM）是通过少量的、不完全的信息，建立数学模型并做出预测的一种预测方法。由于道路交通系统是一个动态的时变系统，具有一定的随机性，灰色系统理论针对时间序列短、统计数据少、信息不完全系统的分析与建模具有较强的针对性。

对原始数据序列作一阶累加灰生成运算，使生成序列呈一定规律更适于建模。 设 X（0）=（x（0）（1），x（0）（2），…，x（0）（n））为非负序列，其中 x（0）（k）≥0，k=1，2，…，n。 记 X（1）=（x（1）（1），x（1）（2），…，x（1）（n））为 X（0）的一阶累加生成序列，计算公式见（1）。

令 Z（1）=（z（1）（2），z（1）（3），…，z（1）（n））为 X（1）的紧邻生成序列，则有背景值构造公式：

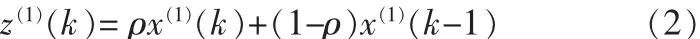
式中，k=1，2，…，n，ρ∈[0，1]。 公式（3）代表的模型：

为GM（1，1，ρ）模型。括号中的第一个参数表示模型的阶次，第二个参数表示变量的个数。参数－a为发展系数，－a的大小和符号反映 GM（1，1）模型对一阶累加生成序列 X（1）的估计值X^（1）和对原始序列 X（0）的估计值X^（0）的发展态势。 参数 b为灰色作用量，反映数据变化的关系。若a^=（a，b）T为参数序列，且有：

则公式（4）的最小二乘参数列满足：

GM（1，1）模型的时间响应函数为：

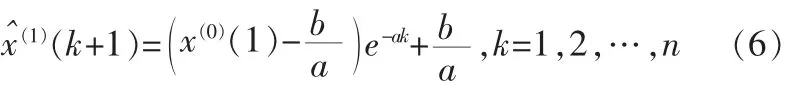
GM（1，1）模型对应的还原值：

即为 GM（1，1，ρ）模型的预测公式[7]。 灰色新陈代谢 GM（1，1，ρ）模型是指每次预测保持相同的数据个数，将得到的新数据直接加入 X（0）序列，同时删除原序列的第一个数据 x（0）（1），即构成新动态序列并建模。由于及时补充了实时观测的新鲜真实数据，因此有效地提高了预测精度。

1.2 遗传算法

遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，它借鉴了达尔文的生物进化论和孟德尔的遗传学说，是一种高效、并行的自适应全局优化概率搜索算法。

图1 遗传算法基本流程图Fig.1 Flaw chart of the genetic algorithm

遗传算法的基本流程如图1所示。首先，遗传算法需要确定所求问题的参数集和解空间，同时根据具体问题确定解空间中个体的编码方式。其次，遗传算法随机产生N个个体组成的初始种群，作为初始迭代点。然后计算每一代种群中个体的适应度，判断是否满足遗传算法的终止条件。最后根据适应度进行选择、交叉和变异等遗传操作，产生新的种群。经过循环迭代，直到满足搜索终止条件，遗传算法使问题解的种群逐步进化到搜索空间中最优或准最优解的区域。遗传算法的基本算子有：

1）编码

编码是将问题的解转化到遗传算法能够处理的搜索空间，是应用遗传算法的首要问题。常用的编码方法有二进制编码、实数编码和符号编码。其中，实数编码的个体的基因位值用一个浮点数来表示，一般采用决策变量的真实值，个体的编码长度取决于决策变量的个数[8]，适合于高精度的遗传算法，便于遗传算法与经典优化方法的混合使用。

2）选择算子

选择算子按照某种原则从父代中选择个体作为子代。选择算子建立在个体的适应度基础上，目的是避免基因损失，提高全局收敛性和计算效率。常用的选择算子有轮盘赌法、竞技选择法、最优保存法和随机均匀法等。

3）交叉算子

遗传算法的交叉算子模仿自然界有性繁殖的基因重组过程来产生新的个体。常用的交叉算子有单点交叉、两点交叉和分散交叉等。

4）变异参数

变异操作模拟自然界的进化过程中染色体上基因位的突变现象，能够保持种群中基因的多样性，使遗传算法的搜索空间更广。常用的变异参数有基本变异、高斯变异等。

1.3 遗传灰色 GM（1，1，ρ）模型

采用遗传算法优化灰色GM（1，1，ρ）模型的背景值参数ρ即获得遗传灰色 GM（1，1，ρ）模型。ρ的取值范围是[0，1]。遗传算法采用实数编码，种群大小为20，随机均匀选择，交叉概率为0.8，分散交叉，高斯变异。遗传算法的适应度函数是灰色GM（1，1，ρ）模型对已知数据估计的平均误差E：

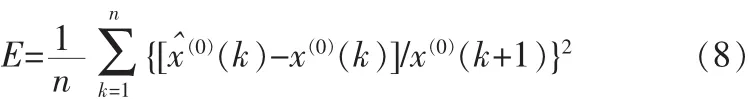
图2是遗传算法优化灰色GM（1，1，ρ）模型背景值 ρ的流程图。

2 实验结果

现以深圳市滨河大道和红岭南路交界处2007年10月26日6:00～7:15的交通流量数据[9]为例，采用灰色新陈代谢GM（1，1，ρ）模型根据已知的4个数据，预测第 5个时间间隔的交通流量。预测结果如表1和图3所示，平均相对误差1.941 8%。

图2 遗传算法优化灰色GM（1，1，ρ）模型参数流程图Fig.2 Flaw chart of the GM（1，1，ρ） model optimized by genetic algorithm

表1 遗传新陈代谢GM（1，1，ρ）模型预测结果表Tab.1 Table of the results of genetic metabolism GM（1，1， ρ）model to predict

图 4 是 GM（1，1，ρ）模型采用 6:05～6:20 的数据预测 6:25时交通流量时，遗传算法优化模型背景值参数ρ的效果图。通过遗传算法优化的背景值ρ=0.498。

3 结 论

文中提出了一种遗传灰色新陈代谢GM（1，1，ρ）模型，采用遗传算法优化灰色 GM（1，1，ρ）模型的背景值参数 ρ，并使用遗传灰色新陈代谢GM（1，1，ρ）模型预测交通流量。通过对实际的交通流量数据的预测结果分析表明，运用遗传灰色新陈代谢GM（1，1，ρ）模型预测交通流量具有很好的预测精度，且具有实时性高、使用数据少等优点，是一种有效的短时交通流量预测方法。

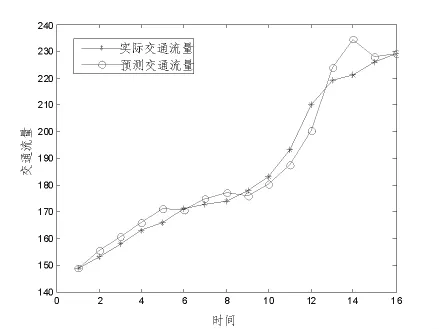
图3 遗传新陈代谢GM（1，1，ρ）模型预测效果图Fig.3 Forecast of the genetic metabolism GM（1，1，ρ） model

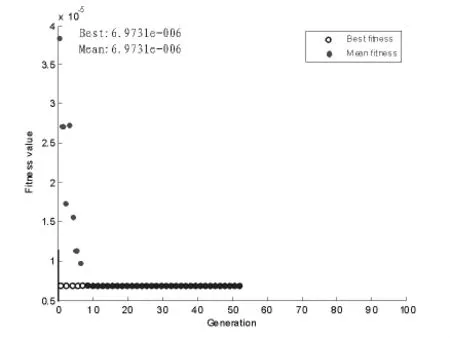
图4 遗传算法优化效果图Fig.4 ρ optimized by the genetic algorithm

[1]严光文，刘静，余振华.基于RBF神经网络的短时交通流量预测[C]//Proceedings of 2010 International Conference on Broadcast Technology and Multimedia Communication，24-27.

[2]高慧，赵建玉，曹磊.短时交通流预测方法综述[J].济南大学学报：自然科学版，2008，22（1）：88-94.GAO Hui，ZHAO Jian-yu，CAO Lei.Summary of short-time traffic flow forecasting methods[J].Journal of University of Jinan:Sc.i&Tech ，2008，22（1）：88-94.

[3]田晶，杨玉珍，陈阳舟.短时交通流量两种预测方法的研究[J].公路交通科技，2006，23（4）:103-106 TIAN Jing，YANG Yu-zhen，CHEN Yang-zhou.Study on short-time traffic flow forecsating based on two different methods[J].Journal of Highway and Transportation Research and Development，2006，23（4）:103-106

[4]罗向龙，牛国宏，潘若禹.交通流量经验模态分解与神经网络短时预测方法[J].计算机工程与应用，2010，46（26）:212-214.LUO Xiang-long，NIU Guo-hong，PAN Ruo-yu.Short-term traffic flow prediction method based on EMD and artificial neural network.Computer Engineering and Applications[J].ComputerEngineeringandApplications，2010，46（26）:212－214.

[5]韩进，王国华，张欣豫.基于神经网络的某仓储库气体质量预测系统[J].电子设计工程，2011，19（18）:75－77.HAN Jin，WANG Guo-hua，ZHANG Xin-yu.Position based on BP network prediction of air quality[J].Electronic Design Engineering，2011，19（18）:75－77.

[6]郭杰，丁镠，朱超余.灰色预测模型的系统动力学仿真[J].电子设计工程，2011，19（14）:4－7.GUO Jie，DING Liu，ZHU Chao-yu.System dynamics simulation of grey models[J].Electronic Design Engineering，2011，19（14）:4－7.

[7]刘思峰，郭天榜，党耀国.灰色系统理论及其应用[M].2版.北京：科学出版社，1999.

[8]高隽.智能信息处理方法导论[M].北京：机械工业出版社，2004.

[9]许大宏.灰色Verhulst模型在短时交通流预测中的应用[J].计算机时代，2011（2）:51－53.XU Da-hong.Application of Grey Verhulst Model in shorttime traffic flow prediction[J].Computer Era，2011（2）:51－53.