无迹卡尔曼滤波算法在目标跟踪中的研究

郝晓静，李国新，李明珠，张亚粉，常晓凤

（长安大学 信息工程学院，陕西 西安 710064）

在目标跟踪中，可靠而精确的目标跟踪是目标跟踪系统设计的主要目的。而对目标跟踪技术的研究，在军事以及民用领域中都有着十分重要的意义。对于目标跟踪问题的解决，不同的学者提出过不同的解决方案。在应用卡尔曼滤波方法解决许多实际问题时，状态方程或量测方程表现为非线性，那么滤波问题也表现为非线性。根据卡尔曼滤波方法，解决非线性滤波问题的最优方案需要得到其系统方程的完整描述。然而这种精确的描述需要无尽的参数而无法进行真正实际应用。为此人们提出了大量次优的近似方法[1-2]。对于非线性滤波问题的次优近似，共有两大途径：1）将系统方程中，非线性部分线性化，对高阶项采用忽略或逼近的方法；2）利用采样的方法，对近似非线性分布和非线性函数进行线性化近似。

1 无迹卡尔曼滤波（UKF）

UKF方法是采用采样策略逼近非线性分布的方法。UKF方法以UT变换[3-5]为基础，采用卡尔曼线性滤波框架，具体采样形式为确定性采样，而非粒子滤波方法[6]的随机采样。UKF方法采样的粒子点（一般称为Sigma点）的个数很少，具体个数根据所选的采样策略而定。UKF采用的是确定性采样，从而避免了粒子滤波方法的粒子退化问题。UT变换是UKF算法的核心和基础。它是计算进行非线性传递的随机向量概率的一种方法。具体变换方法可用图1解释。

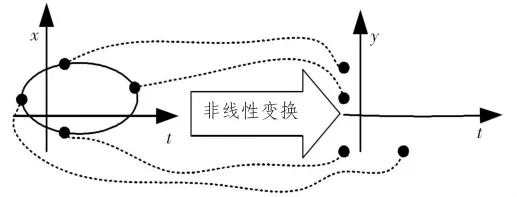
图1 UT变换原理Fig.1 UT transform principle

UT变换的思想是：在确保采样均值和协方差为x和Px的前提下，选择一组点集（Sigma点集），将非线性变换应用于采样的每个Sigma点，得到非线性转换后的点集y和Py是变换后Sigma点集的统计量。

UT变换算法框架[7-8]如下：

1）根据输入变量x的统计量x和 Px，选择一种 Sigma点采样策略，得到输入变量的 Sigma 点集{χi}，i=1，…，2n+1，以及对应的权值Wmi和Wci。其中：2n+1为所采用的采样策略的采样Sigma点个数，Wmi为均值加权所用权值，Wci为协方差加权所用权值。如果不采用比例修正，则Wmi=Wci=Wi。

2）对所采样的输入变量Sigma点集{χi}中的每个 Sigma点进行f（·）非线性变换，得到变换后的Sigma点集{yi}。

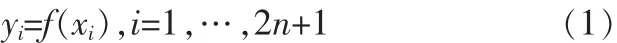
3）对变换后的Sigma点集{yi}进行加权处理，从而得到输出变量y的统计量y和Py，具体的权值仍然依据对输入变量x进行采样的各个Sigma点的对应权值Wmi和Wci。

在对称采样中，由2n+1个对称点来近似估计均值为x和协方差为Px。其中满足要求的附带相应权值的采样点，由下式确定：

其中κ是一调节参数，用来控制每个点到均值的距离，仅影响二阶之后的高阶矩带来的偏差；是矩阵（n+κ）Px平方根的第i列，可以利用乔勒斯基分解进行计算。若Px的矩阵平方根为A，可表示为Px=ATA的形式，则采样点为A的行向量，若Px=AAT，则采样点为A的列向量。Wi是与第i个Sigma点相应的权值。且有：

随着系统维数的增加，Sigma点到中心x的距离越来越远，会产生采样的非局部效应，对于许多非线性函数会产生一些问题，如κ为负数会导致方差矩阵的非正定。比例采样，可有效地解决采样非局部效应问题，并可适用于修正多种采样策略。比例采样修正算法如下：

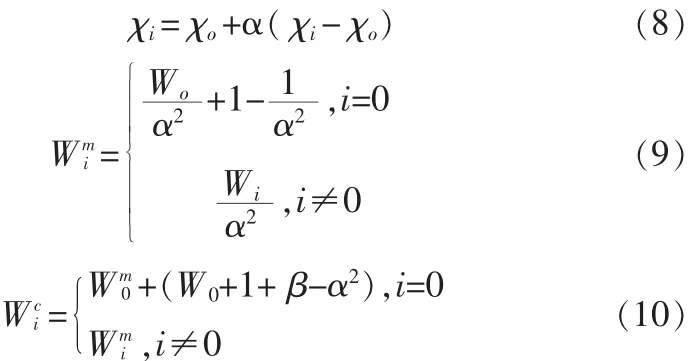
式中：α为正值的比例缩放因子，可通过调整α的取值来调节Sigma点与的距离；β为引入f（·）高阶项信息的参数，当不使用高阶项信息时，β=2。

将比例修正算法应用于对称采样中，得到比例对称采样方法。具体的Sigma点采样公式为：

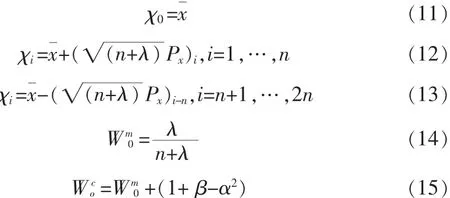
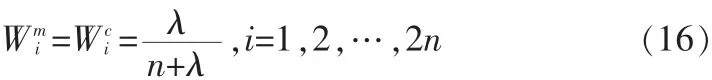
其中 λ=α2（n+κ）-n 是调节参数，控制 Sigma 点与均值的距离。参数确定的一般取值的范围：α决定了采样点x在附近的分布程度，通常取值的范围是10-4≤α≤1；参数β用来描述x的分布新息，对于正态高斯分布情况，β=2是最有效的；而κ是一个比例参数，通常设置为0或3-n。

综上所述，UT变换是将输入变量的统计特性通过非线性系统传播。传播后的均值和协方差矩阵是状态方程真实统计特性的更好逼近，它的计算精度比线性化近似有了很大的提高。由十在计算过程中，它无需进行雅克比矩阵计算，因而实现起来更加简便快捷。

UKF不必线性化非线性状态方程或量测方程，它直接利用非线性状态方程来估算状态向量的概率密度函数。UKF规定一组确定的采样点，当状态向量的概率密度函数是高斯型的，利用这组采样点能获取高斯密度函数的均值和协方差。当高斯型状态向量经非线性系统进行传递时，对任何一种非线性系统，利用这组采样点能获取精确到二阶矩的后验均值和协方差。

设 x 是 nx维随机向量，f：Rnx→Rnx：是非线性函数 y=g（x），假定x的均值和协方差分别是x和Px，利用UT方法计算y的一、二阶矩的步骤[7]如下：

1）计算2n+1个采样点 χi及相应的权值Wmi和Wci。

2）通过非线性方程传递采样点。

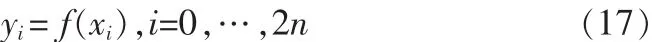
3）估算y的均值和协方差。

在UKF算法中，当需要对噪声进行估计时，需要对状态进行扩维处理。假定在时刻k，状态估计和协方差分别为x^k/k，Pk/k，状态方程和量测方程分别为：

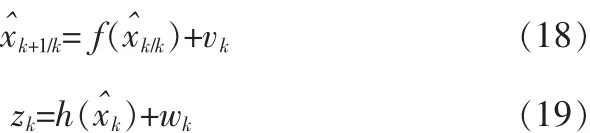
状态初始条件为：

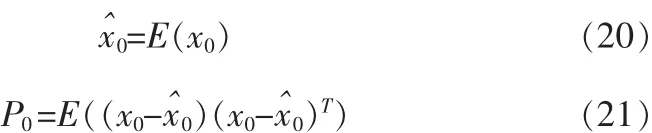
状态的初始条件扩维：

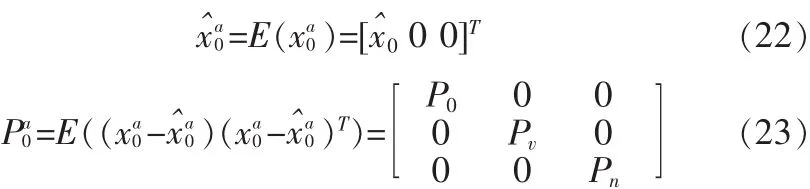
当不要求对噪声进行估计时，即不需要对状态进行扩维时就可以得到简化UKF算法，简化UKF算法只对状态进行Sigma点采样。简化的UKF算法的步骤如下：

1）Sigma点采样，根据UT变换计算状态向量矩阵

采用采样策略，得到 k时刻状态估计的Sigma点集{χk/k（i）}，i=1，…，2n+1和相应的权值Wmi和Wci。其中2n+1为所采用的采样策略的采样Sigma点个数。Wmi和Wci的值如上所述。

2）利用状态方程传递采样点 χk+1/k（i）=f（ χk/k（i））

3）利用预测采样点 χk+1/k（i），权值 Wmi，Wci计算预测均值x^k+1/k和协方差矩阵Pk+1/k

4）利用2）预测量测采样点

5）预测量测值和协方差

这里，Pzz是量测向量协方差矩阵；Pxz是状态向量与量测向量的协方差矩阵。

6）计算UKF增益，更新状态向量和方差

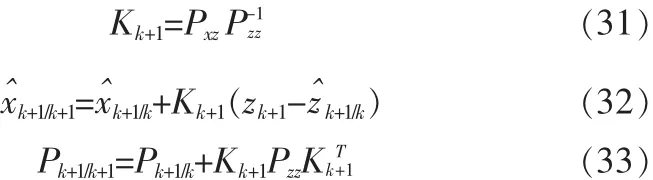
分析上述过程可以看出算法过程主要有2个方面，一方面是对时间的更新另一方面是对量测的更新。该算法适用于任意非线性系统模型，它不需要估算雅克比矩阵，实现简便。

2 仿真实验

仿真一：目标从（1 000 m，800 m，600 m）处飞行，以（200 m/s，250 m/s，300 m/s）的速度和（50 m/s2，30 m/s2，40 m/s2）的加速度加速飞行，仿真飞行的时间为120 s；机动频率α为0.5；采样周期T为1 s；过程噪声的方差为1 600；距离、方位角、俯仰角的测量误差分别为100，1，1；状态向量的维数n=9；初始值的方差矩阵为 diag[1 1 1 1 1 1 1 1 1]。UKF 参数设置 α′=1，κ=0，β=2。 仿真结果如图 2～图 5所示。

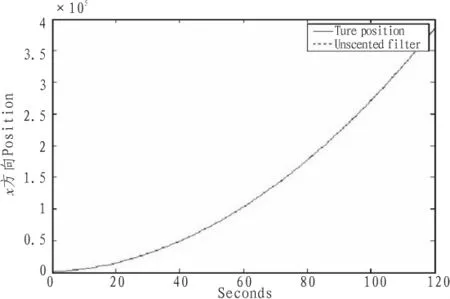
图2 位置的真实值和估计值Fig.2 Position real value and estimated value

图3 速度的真实值和估计值Fig.3 Velocity real value and estimated value

图4 加速度的真实值和估计值Fig.4 Acceleration real value and estimated value

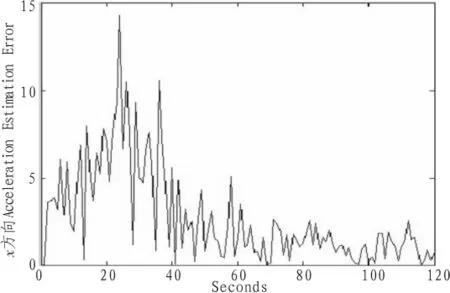
图5 加速度估计误差Fig.5 Acceleration estimate error

从图2～图4可以看出UKF滤波算法对机动目标的跟踪的位置、速度有很高的精度，对加速度大概在60 s时跟踪上机动目标运动的加速度；图5说明加速度的跟踪误差随着时间的增加而在不断减小，在120 s左右误差就接近为0，因此可以得出UKF滤波算法具有很好的跟踪效果。

仿真二：目标从（1 000 m，800 m，600 m）处飞行，以（200 m/s，250 m/s，300 m/s）的速度匀速飞行，仿真飞行时间为 120 s，在前60 s内做匀速运动， 在60 s到120 s以内 （38 m/s2，30 m/s2，40 m/s2）以做匀加速运动。机动频率为0.5；采样周期为1 s；过程噪声的方差为1 600；距离、方位角、俯仰角的测量误差分别为100，1，1；状态向量的维数n=9；初始值的方差矩阵为diag[1 1 1 1 1 1 1 1 1]。UKF 参数设置 α′=1，κ=0，β=2。仿真结果如图6～图9所示。

图6 位置的真实值和估计Fig.6 Position real value and estimated value

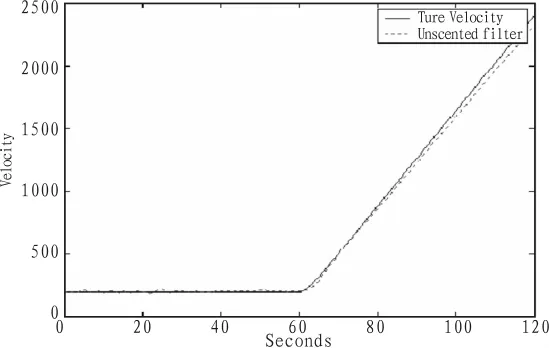
图7 速度的真实值和估计值Fig.7 Velocity real value and estimated value

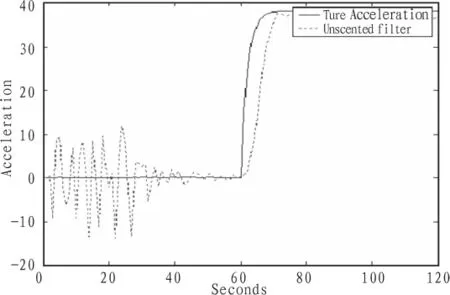
图8 加速度的真实值和估计值Fig.8 Acceleration real value and estimated value

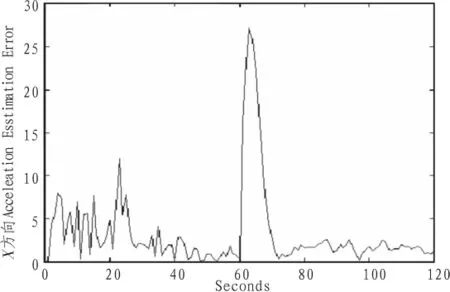
图9 加速度估计误差Fig.9 Acceleration estimate error

由图6～8可以看出，当机动目标在不同的时间段内分别作两种运动时，UKF滤波算法对状态向量在坐标轴x轴方向的位置、速度同样有很高的精度。加速度的估计值在第一段运动的过程中，大概经过30 s就能跟踪上机动目标的加速度，在第二段运动的过程中，在经过30 s左右的时间就能对机动的目标又很好的跟踪。图9表明目标在发生机动的时刻60 s左右由很大的跟踪误差，但经过10左右的时间误差就会相应的减少。因此，可以看出机动目标在不同时间段做不同的运动时，UKF算法对机动目标的跟踪同样有很高的精度和稳定性。

3 结 论

文中对无迹卡尔曼滤波方法进行了分析和总结，无迹卡尔曼滤波方法能有效处理系统方程非线性强度大的情况，滤波精度和稳定性也好于卡尔曼滤波方法，但要求噪声是高斯白噪声。并通过两个仿真例子，对目标跟踪的位置、速度、加速度进行深入分析讨论。仿真结果表明无迹卡尔曼滤波算法对机动目标的跟踪有很高的精度和稳定性。

[1]Maybeck P S.Stochastic models estimation and control[M].New York:Academic，1982.

[2]Jazwinski A H.Stochastic processes and filtering thery[M].New York:Academic，1970.

[3]王志刚，芮国胜，胡昊.UPF算法及其在目标跟踪中的应用[J].雷达科学与技术，2005（2）:21－23.WANG Zhi-gang，RUI Guo-sheng，HU Hao.Unscented particle filter algorithm and its application to target tracking[J].Radar Science and Technology，2005（2）:21－23.

[4]Julier S J，UhlmannJ K.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE，2004，92（3）:401－422.

[5]韩春雷，陈赤联，宋明，等.卡尔曼滤波在被动目标跟踪系统中的应用[J].电子科技，2012（4）：47－50，53.HAN Chun-lei，CHEN Chi-lian，SONG Ming，et al.Application of Kalman filter in passive target tracking[J].Electronic Science and Technology，2012（4）：47－50，53.

[6]朱志宇.粒子滤波算法及其应用 [M].北京：科学出版社，2010.

[7]Julier S J.The scaled unscented transformation.Proc of American Control Conf[C]//Jedderson City，2002:4555－4559.

[8]Julier S J，Durrant-Whyte H F.Navigation and parameter estimation of high speed road vehicles[C]//In Robotics and Automation Conference，1995:101－105.