一种基于阶跃阻抗波导带通滤波器的设计

金海陆，李良荣，李 奇，黄绳雄，张 旭

（贵州大学 理学院，贵州 贵阳 550025）

微波带通滤波器作为无线电通信和雷达系统中的关键无源器件，目前被广泛的研究。现在应用非常普遍的有波导滤波器、同轴滤波器、带状线滤波器和微带滤波器等等。带状线滤波器具有小的尺寸、通过光刻技术易于加工、与其它有源电路元件易于集成等优点，在射频和微波电路中常被使用。但是，当要求滤波器能够承受高功率、低插损、高抑制、窄带宽时，腔体滤波器是最好的选择。但腔体滤波器件最大缺点是——尺寸明显比其他可应用在微波波段的滤波器大。因此紧凑型波导滤波器就成为微波技术领域的一个经典而又十分活跃的研究课题[1-3]。

M.Makimoto和S.Yamashita证实：SIR在不减小无载Q值的情况下可缩短谐振器的长度。作者正是利用阶跃阻抗谐振器（SIR）原理，实现腔体带通滤波器体积的压缩，并且杂散谐振频率被移开[3-5]。

1 阶跃阻抗谐振器的原理

所谓阶跃阻抗谐振器（SIR），是指由2个以上具有不同特征阻抗的传输线组合而成的横向电磁场或准横向电磁场模式的谐振器。 SIR 的 3 种基本结构，如图 1（a）、（b）和（c）所示，它们分别对应的是lg/4型、lg/2型和lg型。基本的SIR结构的共同单元是，都包括开路端、短路端和它们之间的阻抗阶跃结合面。他们分别看成由1个、2个和4个这样的基本单元所组成。在图2所示的SIR基本单元结构中，传输线短路端和开路端之间的特征阻抗和等效电长度分别对应为Z1、Z2和q1、q2。 首先定义阻抗比 RZ=Z2/Z1，随后，通过 RZ系统的讨论了SIR的一些基本特性，比如：谐振条件、谐振器长度、杂散谐振频率以及等效电路[3-7]。

1.1 谐振条件

可以看出，SIR的谐振条件取决于q1、q2和阻抗比RZ，与均匀阻抗谐振器（UIR）的谐振条件相比，SIR设计的自由度将变大。

1.2 谐振器长度

SIR开路端与短路端之间的总电长度为qTA，即

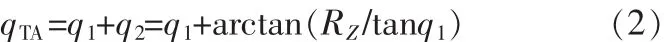
当 0＜RZ＜1、0＜qTA＜p/2 时：得

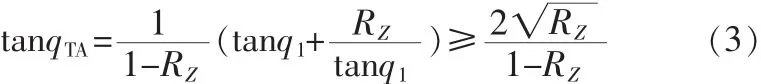
当q1=q2=arctan，qTA取 得 最 小 值 ： （qTA）min=arctan

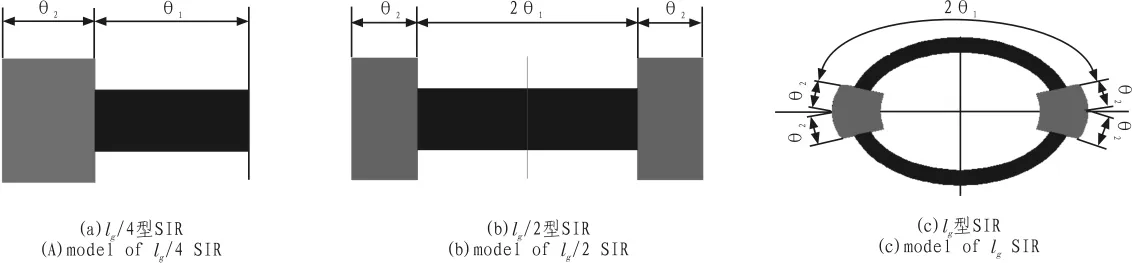
图1 SIR 3种基本结构Fig.1 Three basic structures of SIR

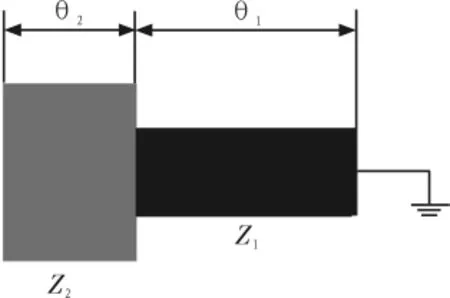
图2 单元SIR的电学参数Fig.2 Electrical parameter of SIR

当 RZ＞1、p/2＜qTA＜p 时，同样可以得到

当q1=q2=arctan时，qTA取得极大值：

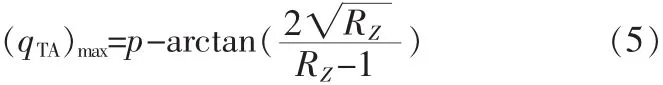
由推导可知，q1=q2是一个特殊条件，它给出了SIR的极大或极小的长度，以后的设计都主要基于这一条件。由此可知，理论上可以用过采用较小的RZ值来无限地缩短SIR谐振器的长度，但是SIR长度被限定于对应UIR长度的两倍。

1.3 杂散谐振频率

设基本谐振频率为f0，lg/4型、lg/2型和lg型SIR相应的最低杂散谐振频率分别为fSA、fSB和fSC，对应的电长度分别为qSA、qSB和qSC。假定SIR结构满足q1=q2=q0，并且忽略谐振器传输线的阻抗阶跃结合面，主导谐振模式为TEM模。

qSA、qSB和 qSC有：

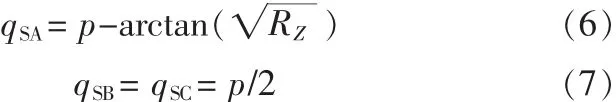
因此，杂散谐振频率为：

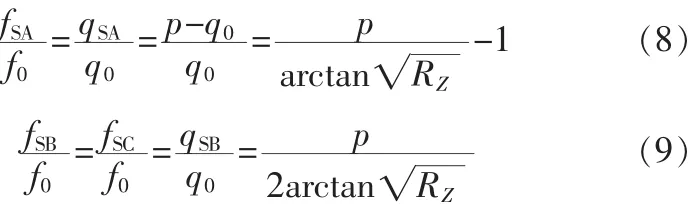
由上面的公式可得：要尽使得杂散频率远离基本谐振频率，优化设计中应取小的RZ值，相应的可以减小谐振器的长度。

1.4 等效电路

在谐振状态下，SIR可以近似等效，等效电路如图3所示。lg/4型、lg/2型和 lg型的磁化率斜率为 bSA0、bSB0，其 bSC0值为：

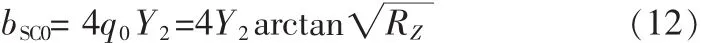
集总参数谐振器磁化率斜率与L0、C0、G0之间的对应关系为：C0=bs/ω0；G0=bs/Q0；Q0:未加 Q 值；L0=1/ω0bs；bs：敏感度斜率参数。

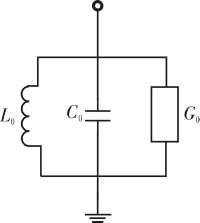
图3 SIR谐振时的等效电路Fig.3 Microwave equivalent circuits of SIR

2 带通滤波器的设计

利用跃阻抗谐振器（SIR）原理，运用HFSS软件对带通腔体滤波器进行建模和仿真，为以后的工程实践提供技术支持。

2.1 滤波器的具体指标

中心频率： f0=780 MHz；通带带宽：Δf=40 MHz；通带差损：S21≥-0.5 dB；驻波：S11≤-20 dB；带外差损： 当 f0±60 MHz时，S21≤-30 dB；体积：110×60×35 mm。

2.2 设计说明

根据上面的技术指标的要求，对于切比雪夫型滤波器，选择级数n=4。为了进一步压缩腔体带通滤波器的体积和方便调试，采用lg/4型SIR结构和调谐销钉相结合的谐振结构。滤波器的设计中常见的耦合方式，如电容耦合、电感耦合、电磁耦合，选择适合于小型化设计的电容耦合方式。谐振器间采用耦合窗和耦合销钉的方式，便于生产调试。

2.3 尺寸表

仿真尺寸（加工实体依据）如表1所示。

2.4 建模及仿真

2.4.1 3D模型

运用HFSS建立的3D模型如图4（a）所示，加工实体如图 4（b）所示。

2.4.2 仿真结果

滤波器的外部耦合采用一种以零相位方式接入的抽头结构。抽头的位置可以通过HFSS仿真来确定：不断的改变输入输出抽头的位置、耦合孔的大小以及谐振器，以得到最好的驻波特性曲线。经过反复的改变抽头的位置，最终得到仿响应及宽频带传输特性的仿真结果。

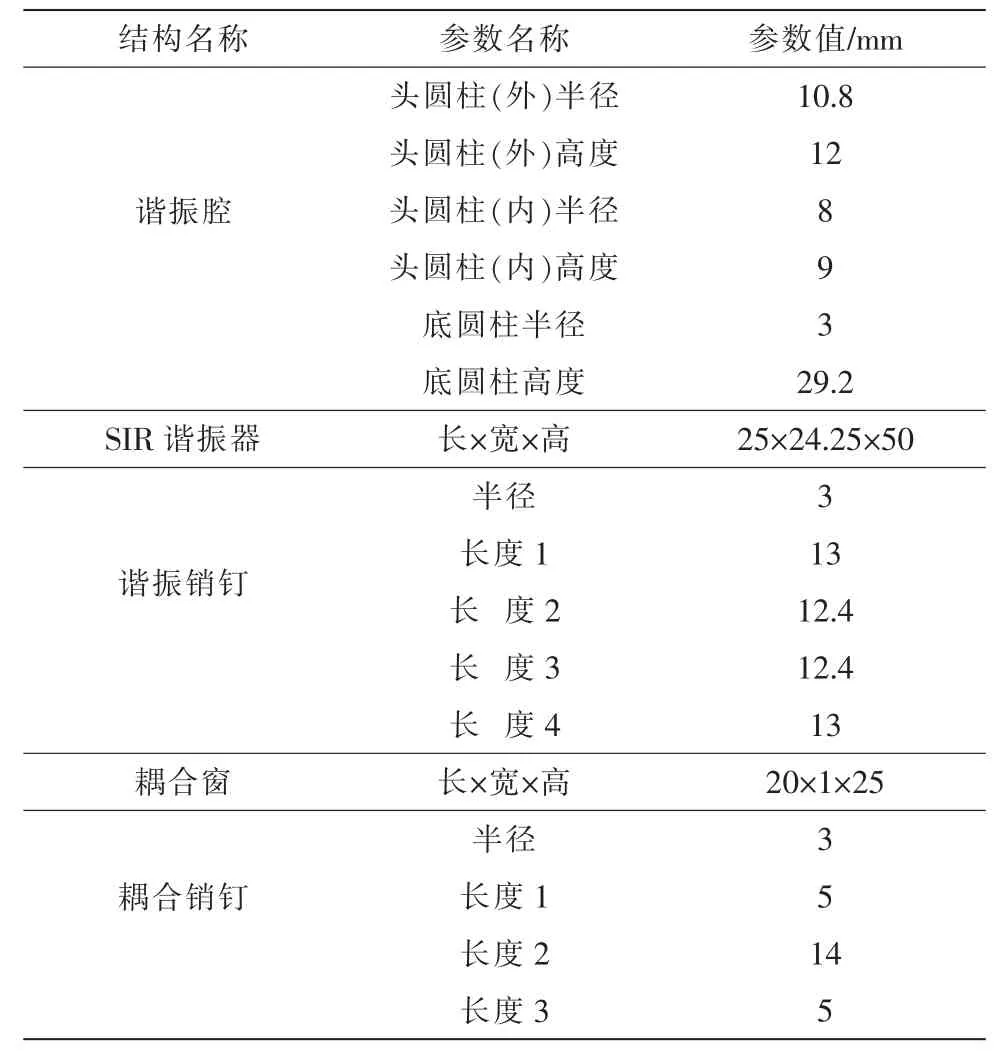
表1 尺寸表Tab.1 Result of dimension

图4 滤波器的实体和模型Fig.4 Model and entity of filter

3 测试及调试经验

真的频响特性曲线，如图5（a）和（b）所示为通带附近的频率

3.1 实体及测试

测试条件：地点：电子科技大学通信学院RFIC实验室；使用的仪器：矢量网络分析仪（型号为Agilent N5230A）。

最后通过调试得到的测试曲线如图5所示。在图6（a）中，可以看出，仿真结果和实际测试结果基本吻合，在3.5 GHz无杂散频率，同时体积也压缩了200%以上。

3.2 波导腔体滤波器调试经验

1）通带内有功损耗的问题

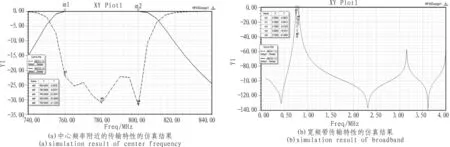
图5 滤波器的仿真结果Fig.5 Simulation result of filter

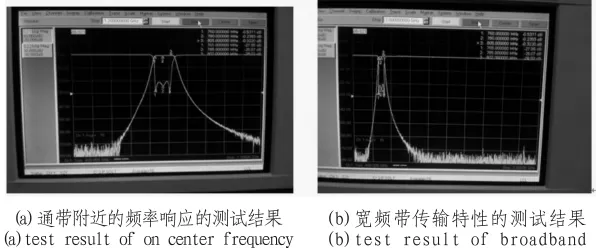
图6 滤波器的测试结果Fig.6 Test result of filter

①对窄带滤波器，上下盖板和侧壁配合是否紧密是减少通带内有功损耗的关键；

②滤波器内表面的光洁度对有功损耗也有明显的影响；

③适当调整谐振柱的长度，使其刚好谐振，调谐螺钉螺纹进入腔内不要太深，以减少有功损耗，并减小温度影响；

④耦合电感近乎插棒处是电流最强处，故必须焊接良好，且必须进行清洁处理，以减小通带内的有功损耗。

2）驻波的问题

制造出的滤波器如果发现驻波过大时，可以适当减小第一腔和最后一腔的SIR谐振结构及谐振腔之间的耦合量，驻波将有所改善。

3）其他问题

窄带腔体滤波器，还必须采用调谐螺钉，否则滤波器中心频率的准确性无法保证；另外在耦合窗增加耦合螺钉，将使谐振腔之间的耦合增加。

4 结 论

结果表明，使用SIR技术设计的腔体带通滤波器，有效的缩小了滤波器的体积，并且该结构也便于生产和调试，另外，滤波器多方面的性能却得到了提高，如通带到阻带下降陡峭度更高、带外抑制性更好、寄生通带更远等。同时，也存在一些问题：差损变差（可以通过提高腔体滤波器内测表面的光洁度，并优化表面的镀层结构得以弥补）。

可以看出，SIR技术可以广泛应用于滤波器的腔体结构中，是实现腔体滤波器小型化的有效方法。

[1]甘本祓.微波传输线设计手册[M].北京：人民邮电出版社，1981.

[2]甘本祓，吴万春.现代微波滤波器的结构与设计[M].北京：科学出版社，1973.

[3]Makimoto M，Yamashita S.Microwave Resonators and Filters for Wireless Communication[M].赵宏锦 译.北京：国防工业出版社，2002.

[4]Kuo J T，Shih E.Microstrip stepped impedance resonator bandpass filter with an extended optimal rejection bandwidth[J].IEEE Trans.On MTT，2003，51（5）:1554－1560.

[5]Sagawa M，Makimoto M，Yamashita S.Geometrical structure and fundamentalcharacteristics ofmicrowave steppedimpedance resonators[J].IEEE Trans.On MTT，1997，45（7）:1078－1085.

[6]Makimoto M，Yamashita S.Bandpass filters using parallelcoupled stripline stepped impedance resonators[J].IEEE Trans.On MTT，1980（28）:1413－1417.

[7]Huang C L，Yen P Y，Weng M H.Planar SIR microwave bandpass filter using high-permittivity ceramics[J].Microwave Opt.Technol.Lett，2000（26）:410－413.