微弱GPS信号差分快速捕获算法

史彦芳，刘 静，马 娟

（西北工业大学 电子信息学院，陕西 西安 710129）

当前GPS作为全球性卫星导航系统在各领域的应用受到普遍关注，尤其是在弱信号环境下的接收定位技术研究，受到紧急救援和军事作战需求的刺激已经成为研究热点，其中的高灵敏度接收技术，由于不受环境和条件的限制尤为受到重视。在高灵敏度GPS接收机中，由于信号的捕获处在基带处理的最前端，因此高效的微弱GPS信号捕获算法是提高高灵敏度GPS接收机性能的关键。通常的弱GPS信号比室外信号强度低约20～30 dB，或在载噪比小于28 dB-Hz则被视为弱信号[1]，普通GPS接收机在这种情况下无法工作，高灵敏度GPS接收机主要通过信号处理算法来获得高的信号处理增益。针对高灵敏度接收机在弱信号的捕获过程中耗费大量时间的问题，文章分析了主要信号累积技术的优缺点，讨论了弱信号环境下GPS信号检测值的概率统计分布特性，利用差分相关所独有的一维搜索特性，结合快速相干累积算法提出了一种新的微弱GPS信号快速捕获算法，并分析了其可行性。通过仿真验证和实际数据测测试，证明算法可行有效。

1 GPS弱信号模型

到达GPS接收机天线的信号经低噪声放大、带通滤波、变频、A/D转换后得到包含各种干扰的数字中频信号。考虑弱信号捕获当中以研究C/A码为主，忽略P码，则中频信号仿真的数学模型为[2]。

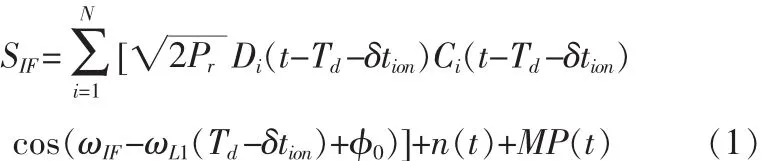
其中，t为GPS时间；ωIF为中频角频率；收信号幅值；Di（t）为卫星 i的导航电文；Ci（t）为第 i颗卫星对应的 C/A 码；MP（t）为多径干扰；tion为电离层延时；Td为卫星时钟偏差、星历误差等引起的时延；传输时延表现在接收的信号中导航数据、C/A码和载波相位发生相应变化。同时可根据文献[2]中给出的多普勒频移模型和噪声模型，可对微弱GPS信号的特性进行深入分析，从而设计更有效的捕获算法。

2 GPS弱信号累积算法的性能分析

在微弱GPS信号捕获算法中，信号累积技术是提高处理增益的关键。当前基本的信号累积技术可分为3类：相干累积、非相干累积和差分累积，其中信号经相干累积处理获取的增益效果最佳，但其应用受到导航数据比特翻转的限制，如累积过程中遇到数据比特翻转性能会有所下降；非相干累积和差分累积的提出就是为了克服和减少这种影响，但需付出不同程度的信噪比损失作为代价，并且原始信号越差它们的信噪比损失越大，因此只能与相干累积结合使用。目前微弱GPS信号捕获算法均是以信号累积理论为基础，如半比特捕获算法和全比特捕获算法[3]，通过估计数据比特跳变来进行长相干累积的捕获算法[4]，以及在对三种数据累积技术分析比较的基础上提出的相干累积与差分检测相结合的方法[5]等，这些算法的改进均是为了提高对微弱GPS信号的捕获性能，以使高灵敏度GPS接收机实用化。因而，在这里我们尽量延长相干累积的时间，从而最大限度的提高信号的处理增益，捕获更加微弱的GPS信号。

2.1 差分累积

差分累积作为一种新的弱信号累积技术，其在高灵敏度接收机中的应用逐渐受到关注。差分累积的相关运算采用比较新颖的差分式相关，然后再将多个周期的相关结果进行对应叠加。差分相关法又称延时相乘法，由于该算法是在复数模型下推导运算的，因而实际当中，首先将传统的I、Q两个支 路 下变 频 后 的数 据 ，以 SIF，I（n）+jSIF，Q（n）的 形 式 构 造 一 个 复 数型数字中频信号。

差分相关首先将复数数字中频与其延迟后的复数共轭相乘，同时接收机的复制C/A码也与其延迟后的复数共轭相乘，然后用这两个结果进行相关运算[6]。假设某颗卫星的数字中频信号 SIF（n）可表示为

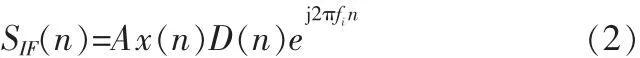
其中，x（n）与D（n）分别为卫星C/A码与导航电文数据比特，fi为接收信号的数字中频频率。数字中频与其延迟共轭的乘积为

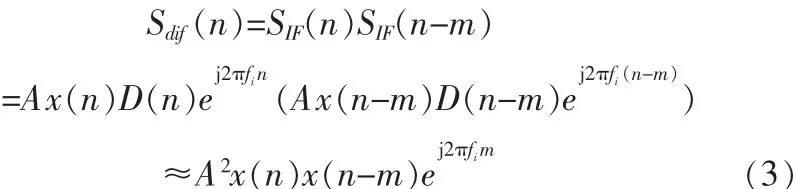
对本地复制 C/A 码 c（n）进行相同操作，则与 sdif（n）进行相关的 cdif（n）为

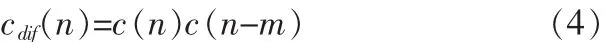
由式（3）可得出差分相关运算的两个特点：第一，接收的数字中频信号经过差分后，数据比特D（n）经平方后被消去；第二，由于 ej2πfim是不随时间变化的常数，因而差分后的信号中载波频率也被消除。基于以上原因，差分相关后的数据累积不再受到20 ms导航数据比特的限制，同时由于差分信号中不含载波，在对卫星信号搜索时，可以直接获得接收信号的码相位。载波分量经过差分运算后变为常量，使得相关运算后的数据累积结果不再受多普勒频移的影响，不会因多普勒频差的存在而降低相关峰值。差分相关运算将卫星信号的二维搜索确认过程，变为仅在一维内搜索，因而极大的提高了对卫星信号的搜索确认速度。

2.2 累积算法性能对比

由于3种累积方式的不同特性，在低信噪比环境下，单独的使用一种累积方式，很难获得理想的捕获性能。为了平衡算法效率与信号捕获效果，通常是将相干累积与另外两种累积算法结合使用，或在基本的累积算法基础上进行改进，以克服其存在不足，使弱信号累积算法具有更好的性能。

在改善检测统计量信噪比方面，相干累积的效果是最好的，差分相干累积捕获算法其次，非相干累积最差。因为相干累积时信号功率呈平方倍增长，噪声功率仅是线性增长，使得信噪比线性提高；差分相关捕获算法对相邻相干累积值的共轭相乘再累积会使信号部分增强，但信号和噪声的交叉乘积项成为新的噪声，它对信噪比的改善不及相干累积；而非相干累积把信号和噪声作平方处理再累积，由于平方损失（squaring loss）噪声部分被放大，对信噪比的改善效果最差。若在低信噪比环境下应用非相干累积算法，要么检测性能很差，要么必须通过大幅增加累积次数来抬高信噪比，这样会延长捕获时间。

在捕获时间方面，相干累积由于sinc（πΔ fT）中Δ f的限制，频域搜索的步长较小，频域搜索次数增多，整个搜索时间较长。而差分相关捕获算法和非相干累积算法都在相干累积后进行了第二次累积以提高信噪比，因此，相干累积时间T可设得较短，Δ f的限制也可相应放宽，频域搜索步长可加长，捕获时间比相干累积算法短。

在实际的算法设计中，都是以1 ms相关结果矩阵为基本单元。然后根据提高处理增益的累积方式，进行累积处理。非相干累积的基础是相干累积，同样差分相干累积的基础也是相干累积。

自我超越是创建学习型组织需要的重要技能之一，是指通过加深对个人愿望的理解，从而促进精力的集中。在此过程中培养和锻炼自己的耐心与责任心，不断结合客观实际，加强对个人能力拓展的学习，充分发挥想象力和创造力，共同完成最终想要实现的目标，取得最佳成绩，并且要营造出和谐的组织环境，激励组织成员能够充分发展自我，不断为自己选择的目标奋斗，实现愿望。

3 新算法的设计

通过对导航电文数据的分析，可发现导航数据编码规则中，通过特殊的运算规则使得在帧同步字之前的交接字的最后两个比特始终为00，来保证接收机收到的帧同步信息始终为10001011，因而在接收数据的帧同步位置可预知的接收比特为0010001011共10的比特。综合考虑算法效率和捕获灵敏度等综合因素，利用导航数据中已知的与帧同步相关的信息和快速相干累积的思想，充分利用差分相关时可快速进行一维搜索的特性，设计算法整体方案如图1所示。

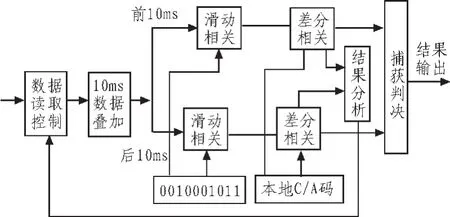
图1 算法捕获方案设计Fig.1 Algorithm capture scheme desig

算法的具体实现步骤如下：

1）每次控制读取160 ms的GPS数字中频数据，并进行以10 ms为单位的数据直接叠加；

2）分别将两组叠加数据与本地10比特帧同步信息进行滑动相关，当接收数据当中含有帧同步信息时，相关操作会获得与之相对应的信号处理增益；

3）将上步获得的数据与本地C/A码进行差分相关运算，得到捕获运算结果；

4）分析捕获结果，控制数据读取的位置，从而找到帧同步码提高信号处理增益；

5）输出捕获判决结果。

3.1 数据直接叠加

3.2 捕获判决

由算法的捕获步骤可知，算法读取数据后实际是对一组10比特数据进行交替半比特相干累积，而导航数据比特翻转要么在奇数组数据中，要么在偶数组数据中。对于存在数据比特翻转的数据组，其最终捕获运算的结果幅值能量应当小于另外一组。对于捕获结果的判决采用成熟的tang搜索算法，其流程如图2所示。

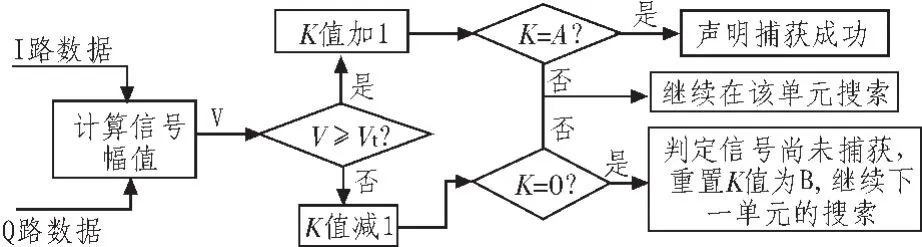
图2 tang搜索算法Fig.2 Tang search algorithm

当捕获程序对信号进行粗捕获，人为某一搜索单元可能存在卫星信号时，则使用tang搜索捕获算法，在同一搜索单元多次搜索对信号进行捕获判决。算初始时设定一初值K，对设定的一组数据进行多次捕获判决记录分析，当捕获幅值V超过捕获门限Vt时K值加1，否则K值减1，当K=A（A为一设定值）时，则人为该信号存在，并成功捕获；当K=0时，则人为该信号不存在，捕获失败。

3.3 差分码的快速构建

在使用差分相关算法进行捕获运算时，由于要构建新的差分码是捕获中新增的运算量，因而这里采用文献[8]中的思想，基于块处理方法，利用常规数字匹配滤波器捕获结构进行新差分码的生成。在n和，n－1时刻CDMF输出表达式为：

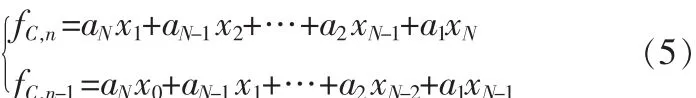
其中，xi为接收到的数字信号，ai为本地伪码序列。由于本算法采用的是GPS基带数据保持不动、本地伪码序列作循环移位结构，故式（5）应改写为

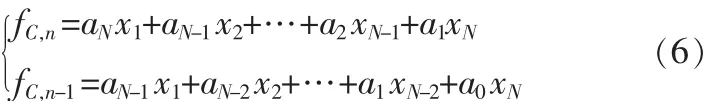
由于C／A码的周期性可得a0=aN，两式相减，得到一个新序列为

由式（3）可知，fC，n可由 fD，n和 fC，n－1获得，差分码 di为

显而易见，差分码di的取值范围只有+2、－2和0 3种，当差分码为0时，是不需要乘法运算的。在这里将差分码di中非零各项的位置和数值分别用pj和ej表示，其中j=1～k，K为差分码di（i=1～N）中非零项的个数。由文献[9]的推导，差分码中数值为0的个数为2r－1－1（r为PN码生成多项式的阶数），所以本算法中所需乘法运算的次数K=2r－1，约为CDMF所需数量的1/2。特别是当每个码片采样为M点时，相乘累加运算量降低为常规方法的I/2M，大大降低了系统所需乘法器的数量。经过对GPS卫星32个C/A码序列的分别计算，K取值范围为480～544，与GPS中频信号采样频率和C/A码初始相位无关。

4 算法性能验证

通过GPS中频信号采样器，将普通环境下接收到的GPS卫星信号进行中频采样后，对同一组数据分别用普通捕获算法和本算法进行捕获。采用普通捕获算法对采集到的GPS信号进行捕获的结果如图3所示。当在采集信号中加入22 dBW的高斯噪声后，普通捕获算法的捕获结果如图4所示，而采用本文捕获方案的捕获结果如图5所示。

图3 普通捕获算法的捕获结果Fig.3 Capture algorithm capture results

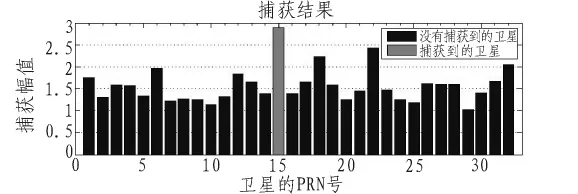
图4 加入噪声后普通算法的捕获结果Fig.4 Adding noise common algorithm for capturing results

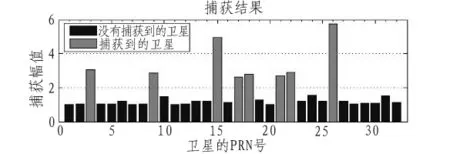
图5 信号中加入噪声后本文设计方案的捕获结果Fig.5 Signal adding noise this paper design capture results

通过上面的对比可以看出，在接收的采样信号中加了仿真噪声后，信噪比降低的情况下，使用普通捕获算法只能捕获到一颗较强的卫星信号。而本文提出的弱信号捕获算法，可以稳定的捕获到低信噪比下的卫星信号，使接收机在弱信号下的定位解算成为可能。采用本算法后多捕获到的较弱的卫星信号，可显著提高GPS接收机灵敏度的同时有效提高定位精度。

5 结束语

通过理论分析算法效果验证，证明本捕获方案具有速度快和灵敏度高的特点，可稳定的捕获信噪比为－42 dB的微弱GPS信号。在低信噪比下，方案中利用GPS数据中帧同步相关的已知信息，有效克服导航数据翻转对相关累积的影响，大大提高了信号处理增益。仿真结果显示，该捕获方案的捕获灵敏度在使用tang搜索捕获判决之后，更加准确的捕获信号。由于采用了快速累积及快速的差分码构建方法，是的本方案在同等条件下的捕获速度明显优于同类算法。

[1]谢刚.GPS原理与接收机设计[M].北京：电子工业出版社，2009.

[2]LEI Dong.IF GPS signal simulator development and verification[D].Calgary University，2003.

[3]PSIAKI M L.Block acquisition of weak GPS signals in a software receiver[C]//ION GPS，Salt Lake City， 2001.

[4]Wang C.，Jia Z.，Wang H.， Continuous integration based navigational signal acquisition:United States，US 7180446[EB/OL].（2007-02-20）.http://www.google.com/patents/.

[5]SHANMUGAMSurendranK，NielsenJ，LachapelleG.Enhanced differential detection scheme for weak GPS signal acquisition[C]//ION GNSS 2007，Session C1，Fort Worth，2007.

[6]皮亦鸣，张婧，蔡昌听.GPS信号的差分相关捕获算法研究[J].全球定位系统，2006（4）:1-4.PIYi-ming，ZHANG Jing，CAIChang-ting.GPS signal differential correlation acquisition algorithm for[J].Global Positioning System，2006（4）:1-4.

[7]Liu K C，Lin W C，Wang C K．A pipelined digital diferentia matched filter FPGA implementation＆ VLSI design[C]//Custom Integrated Circuits Conference，Proceedings of the IEEE，l996．

[8]高胜友，吴硕.采用GPS同步技术和电磁感应原理的电缆识别方法[J].陕西电力，2011（9）:27-29.GAO Sheng-you，WU Shuo.Cable identification based on GPS simultaneous techniques and electromagnetic induction principle[J].Shaanxi Electric Power，2011（9）:27-29.