网络分析法在物流服务供应商选择中的应用

1.引言

物流服务中供应商的选择在供应链管理中是一项非常重要的问题。供应商的价格和质量很大程度上影响着最终消费商品的价格和质量，同时也决定了最终产品竞争、市场份额以及市场可行性。同时，供应商也影响了制造商交货时的成败、产品类型、产品设计差异等方面。至于企业，早已高度重视选择供应商时的弹性。科学合理的选择供应商影响着产品弹性增加、成本降低以及竞争增强。

层次分析法(AHP)广泛应用于处理多指标决策问题。但是AHP方法重大局限是在不同决策原则下的假设独立性。ANP则抓住了决策因素内部依赖关系，支持系统分析，还支持承载着最优决策的相关原则的引入。与AHP相比，ANP在决策过程中提供了更多一般模型，而没有关于一定程度上从低层次到更高层次因素独立性的假设。尽管有以上优势，ANP在决策时的应用还未普及。

近年来，ANP在处理多指标决策问题的应用逐步提高。选择供应商时，要综合考虑类型、主客观因素。这些原则也有一定的内部相关性，并且不能被AHP方法分析。因此，本文推荐选择供应商时以ANP基本模型替代用广泛应用的AHP方法来处理此类问题。

2.文献综述

文献综述主要是为了确定在选择物流服务供应商时的原则。形成初始框架，以便构建选择供应商的ANP基础模型。

2.1 供应商的选择原则

Dickson在1996年系统地研究了供应商评价指标，此后，很多学者开始研究供应商的选择问题。1991年，Weber对物流服务供应商的选择问题的文献进行了统计分析，指出价格、准时交货及质量是主要的三项原则，同时也是重要的评价指标。另外，生产能力、地理位置、技术水平、行业声誉等评价指标也会用到。随着经济全球化加剧，企业的生存环境日趋复杂，柔性成为供应商选择的一项重要指标。因此，文章选择质量、价格、弹性及地理位置、技术水平、资本等因素作为选择供应商的指标。

2.2 网络分析法

网络分析法是一种基于两两比较的思想解决排序问题数学理论方法。ANP能解决系统内部高度独立性的问题及反馈关系，因此我们可以准确地处理复杂的实际问题。能够用于考虑供应商选择因素（明确的或隐含的）及因素独立性反馈关系。这对供应商的选择是一项较好的解决途径。

网络分析法是一个综合决策技术，它涉及了所有相关指标，承接着最终结论。AHP法作为ANP的开端。AHP在组群决策时的优点如下：1)有形资产与无形资产、个人价值和共同价值都被概括在内；2)群组决议选择更侧重目的性；3)结论能够建模，可涉及到每个相关因素。虽然AHP有这些优点，但ANP是更全面的决策模型，没有对从低水平到高水平、同等水平间因素独立性的假设。不同层次指标之间的一个双向箭头或弧线可以代表在ANP模型的相互依存关系。如果相互依存关系是在同一水平的分析，可用于环形弧代表对等的相互依存关系。

3.网络分析法在物流服务供应商选择中的应用

根据前文分析，文章选择质量、价格、柔性以及地理位置、技术水平、财务状况等因素作为供应商选择的指标。在指标与反馈关系独立的情况下，ANP方法应可用于供应商的选择。在ANP方法应用之前，案例公司选定三个潜在供应商。为了使潜在供应商的能力更清晰，可在他们的网站验证基础设施及其他设施，将搜集到的信息用于比较矩阵。ANP方法的应用有以下几个步骤：

3.1 确定指标

首先要准确描述决策问题，目前已有很多文献研究供应商选择的相关原则。这些原则是ANP模型发展的基础。详见表1。

3.2 建立网络

指标网络如图1所示，典型ANP网络包括两部分：一是控制方或者是目标层、指标层；另一部分是网络层，是一层被称为销售基础的部分，在相应的目标中反映出来。指标网络元素或者组织内部元素互相反馈。另外，建立在不同指标上的ANP方法，是在子网上构建的，每个子网反映了相应的控制因素群。

3.3 决定因素的成对比较

在这一步，一系列成对比较用来说明实现这一目标的决定因素的相对重要性。在这种比较下，1—9的比例规模用于比较任两个因素。1分表示两个因素平等重要，9分表示一个因素（列因素）比另一个因素（行因素）有绝对重要性。如果一个因素比它的对比因素影响弱，分数排列会是从1到9，1表示不重视，1/9表示列因素对行因素的绝对重要。对于反向比较，矩阵内的互惠值自动分配，因此矩阵AijAji=1。

物流服务供应商在决定ANP网络中，首先需要建立无权重矩阵，即建立比较因素然后使其指标化。如果“灵活性”作为主要指标，“供应商1”作为第二指标，可反映在表2矩阵里(表1～3作为成对比较中1到9的分值)。

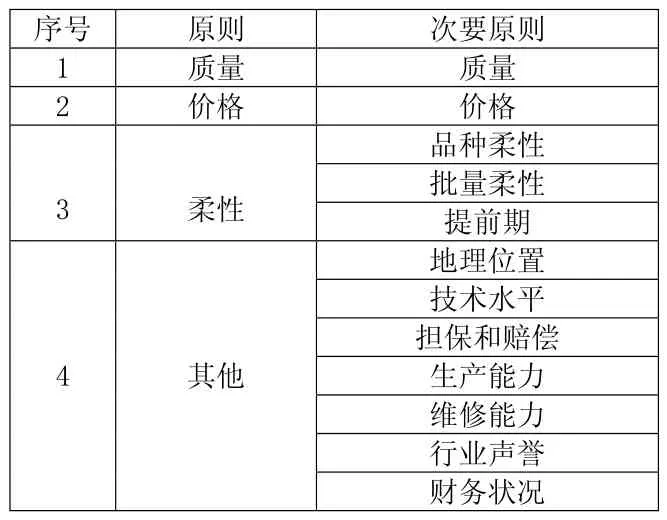
表1 物流服务供应商选择原则

表2 供应商1指标的灵活性矩阵

表3 供应商各种灵活性指标矩阵

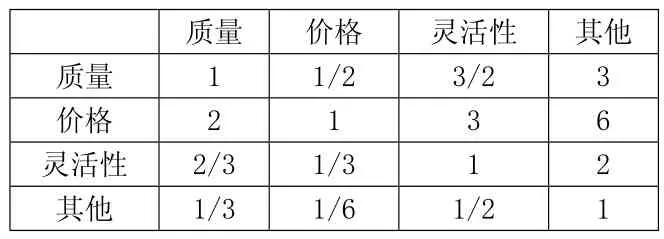
表4 供应商指标矩阵

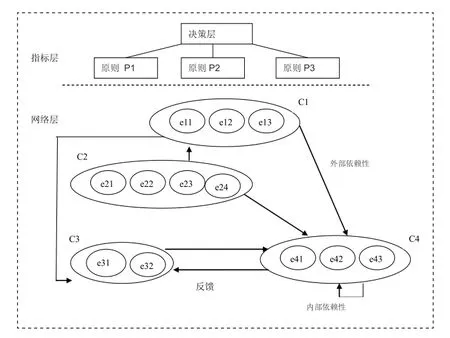
图1 典型ANP网络

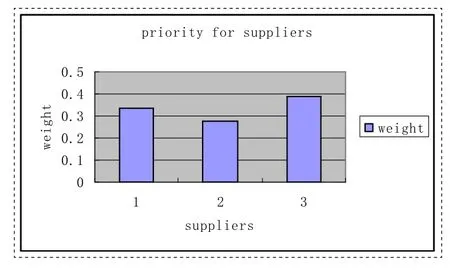
图2 物流服务供应商优先权

矩阵反映了一系列量灵活性下的供应商，量灵活性和能力、资本以及交货时间。但是和其他两类灵活供应商比较，该矩阵没有反映各种灵活供应商。此时，选择供应商主要指标、灵活性是次要指标，如表3的对比矩阵。

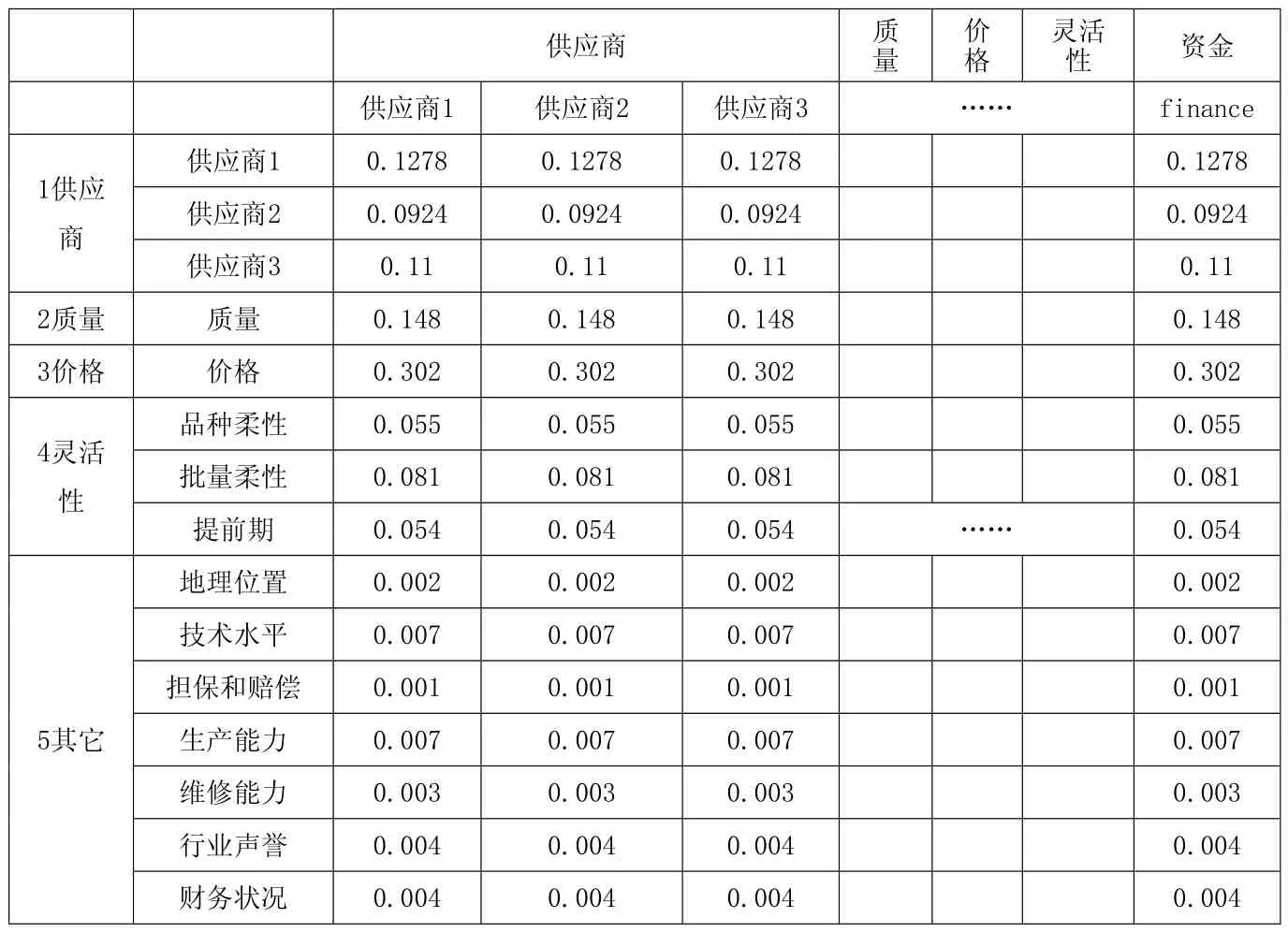
表5 有限矩阵

多重比较矩阵建立后，判断矩阵从极右的权重矩阵指标化。它不能重组后两组之间的超级矩阵的元素，如“替代供应商”作为一个组中的任何两个元素的指标，如表4显示了比较矩阵。

3.4 形成超级矩阵

超级矩阵允许一个系统的元素之间存在相互依存。它是一个分块矩阵，每个子矩阵都是由一套以供应商模型为代表的水平之间或内部的关系组成。超级矩阵如表5，代表每个兼容性行列式推动者的相对重要性措施的结果。

根据各组指标内容的比较，接受矩阵标准化，然后没有重量重矩阵的乘法，你可以得到权重矩阵。根据加权矩阵，可以得到最终表5的有限矩阵。超级矩阵中的元素的相互依存关系来源于成对比较矩阵。

4.结论与建议

从图2可以看出，0.1278，0.0924，0.110表明这三个值可以进行标准化的各供应商的优先显示。供应商优先选择顺序为：供应商1，供应商3，供应商2。拟议的方法使得一个复杂多准则的决策问题简化。它也可以用来量化许多主观判断，这是必要的，以评估不同的替代供应商。这种方法的另一个好处是，它不仅支持集体决策，但也使我们能够记录在决策过程中的种种考虑。如果结果是要传达给各种利益集团，那么这个文件是有用的。

通过ANP的办法来解决物流服务供应商选择问题，如反馈网络间的依赖关系。ANP的方法是在更真实的情况下，提高了物流服务供应商优先选择的准确性，最终使物流服务供应商的选择更加科学。

[1]Saaty T L.Decision making with Dependence and Feedback:the analytic network process[J].Pittsburgh,PA:RWS Publications,1996.

[2]Weber C A.Current J R.Benton W C Vendor selection criteria and methods[J].European Joural of Operational Reasearch,1991(01).

[3]王能民,孙林岩,汪应洛.绿色制造模式下的供应商选择[J].系统工程,2001,3:37-41.