小波去噪在缓变机械故障检测中的应用

2012-01-13

电子世界 2012年19期

91619部队余道友

1.引言

由于机械振动信号本身的复杂性，在接收和处理机械振动信号的各个阶段都可能引入噪声。各种形式噪声的存在会使有用的信号完全淹没在噪声中，从而造成信噪比严重降低，这会给后期的数据处理和分析带来很多不便。传统的降噪方法的原理是将原始信号进行频谱分析，根据有效信号与噪声的频谱范围不同，选择合适的滤波器来去除噪声干扰，保留有用信号。然而在实际的机械振动信号处理中，会遇到噪声与有用信号的频率范围有重叠的情况，如果采用传统的滤波方法虽然能去除噪声，但同时也把有用信号中与噪声频率范围重合的那部分信号去掉了。并且实际检测到的机械振动信号，都属于瞬时激发的非平稳性信号，如果想要处理和分析其特征信息，用傅里叶变换或者短时傅里叶变换的方法都不能保证准确有效的时间分辨率和频率分辨率[1-5]。因此，本文选择小波变换的方法对机械振动信号进行去噪处理，并对实验室所测数据进行了验证。

2.小波去噪基本原理

小波变换是把一称为基本小波的函数ψ（t）做位移τ后，再在不同尺度a下与待分析信号x(t)做内积：

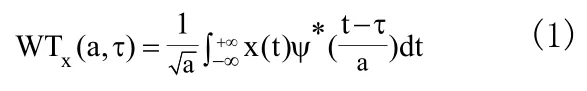
式中，a ≥ 0，X(ω)、ψ( ω)分别是x(t)、ψ（t）的傅立叶变换，a称为尺度因子，τ为平移因子，为归一化因子。

根据信号和噪声在小波变换下的变化规律不同，通过小波变换将信号分解成不同频带和时段内的成分，如果噪声信号和真实信号位于不同的频带内，则只要将噪声所对应的那一阶小波系数按阈值进行处理，然后按重构公式对信号进行重构就可以达到信号滤波的目的。如果噪声信号和真实信号位于相同的频带内，则通过多层分解将一个信号分解成为低频部分和高频部分，如果信号的主要特征包含在比较稳定的部分，即低频部分，高频部分即为其它干扰信息。依照干扰出现的时间变化，对干扰部分进行分时段加权衰减，对有效成分保留，然后将处理后的高、低频成分重构即得到压制噪声后的信号。如果信号的大部分噪声能够分解到某一频带内，那么就将这一频带的信号加权衰减或全部置零，然后进行小波重构，即达到噪声压制的目的。

因此，机械振动信号小波变换去噪过程可总结为如下几个步骤[1-7]：

（1）对信号进行小波分解。选择一个小波函数并确定分解层数N，对信号S进行N层小波分解。

（2）小波分解高频系数的域值量化。对1-N层的高频系数，选择一个阈值进行阈值量化处理。

（3）信号重组。小波分解的第N层低频系数和经处理后第1～N层高频系数，进行信号小波重组。

在小波阈值去噪过程中，阈值选取[5]的优劣，直接影响着降噪的效果。如果阈值选取过大，虽能减少重构信号中残留的噪声部分，但会使信号有较大的失真；反之，减低阈值能减小重构信号的失真，但恢复的信号中残留的噪声也增多了。选取的阈值必须刚好大于噪声的最大水平，通常选取阈值：

式中，σ为噪声信号标准差，也是噪声强度，N为信号长度。

当第m层第n个系数ωm，n小于该阈值时，认为这时的ωm，n主要是由噪声引起的，将系数ωm，n减小至零；当ω m，n大于该阈值时，认为这时的ωm，n主要是由信号引起的，该系数予以保留，从而实现信噪分离。

在实际应用中，噪声强度是未知的，需要进行估计，可以利用小波系数估计噪声标准差：

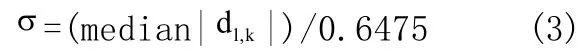
式中：median|dl,k|表示取尺度l上的小波系数的中值。当然，这个阈值不是最优的，根据噪声的小波系数幅值随分解尺度的增加而减小的特性，对得到的阈值T进行改进，使之随尺度变化。

式中：j为尺度；λ为尺度j上的阈值。

对于阈值的选取有：Rigrsure，Heursure，Sqtwolog和Minimax等4种阈值选择规则。其中，Rigrsure是一种基于史坦的无偏似然估计原理的自适应阈值选择，Sqtwolog采用的是一种固定阈值选择，Heursure采用的是最优预测变量阈值选择，Minimax采用极大极小原理产生阈值选择。

3.振动信号频谱分析

3.1 背景噪声频谱分析

在实验室环境下，利用三轴振动传感器对机器的振动信号进行采集和处理，由于排除环境干扰的影响，背景噪声相对较小。实验中振动传感器测量了一组背景噪声，其频谱分别如图1所示。

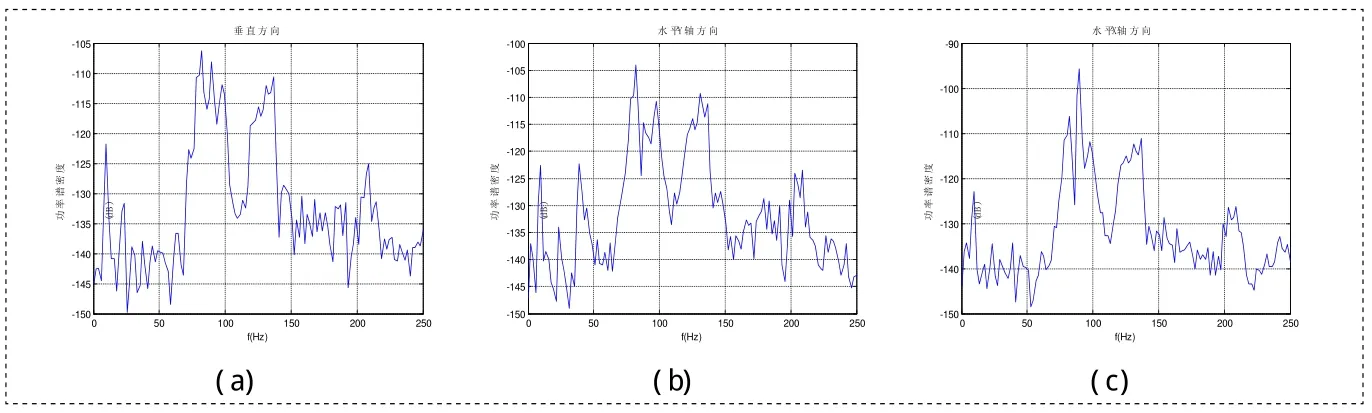
图1 振动传感器检测噪声的功率谱

图2 振动传感器垂直轴检测信号的功率谱图

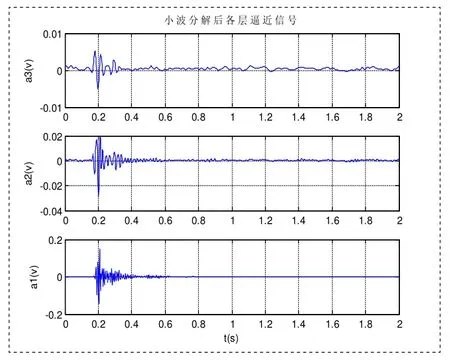
图3 小波分解后各层逼近信号

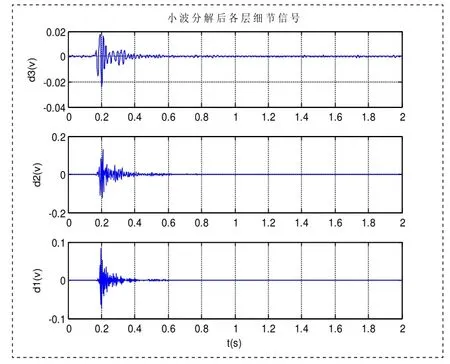
图4 小波分解后各层细节信号

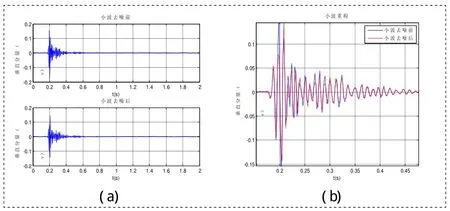
图5 垂直分量小波去噪前后对比图

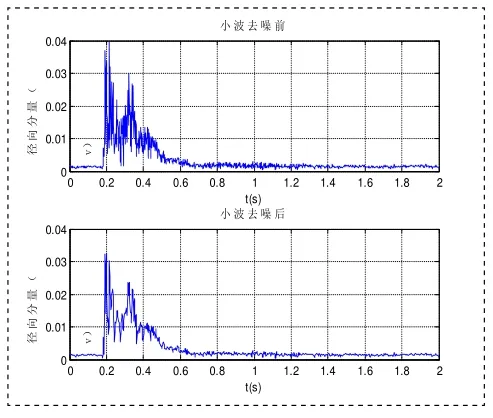
图6 水平分量X轴小波去噪前后对比图

从图1中可以看出，振动传感器获取的背景噪声频谱分布差别不大，检波器三个轴检测的背景噪声都主要集中在70-140Hz频率范围内，这一频段的背景噪声的功率谱都超过了-120dB。从图1中还可以看出，除了图1(c)中所示水平X轴分量中90Hz的噪声功率谱超过了-100dB，其余都在-100dB以下。

3.2 接收信号频谱分析

对振动传感器接收到的信号进行功率谱分析，其三轴分量的频谱分析结果如图2所示。

从图2(a)中可以看出，信号的垂直分量功率谱在-100dB以上的信号分布在23-41Hz和59-174Hz频段内。从图2(b)中可以看出，信号的水平Y轴分量功率谱在-100dB以上的信号在33-49Hz、65-75Hz、80-82Hz、86-102Hz、106-119Hz和133-148Hz频段内。从图2(c)中可以看出，信号的水平X轴分量功率谱在-100dB以上的信号在24-156Hz频段内。

从上面的机械振动信号频谱分析中可以发现，信号的频谱范围比较大，频带宽度达到100Hz以上，既有低频成分又有高频成分。通过与背景噪声的频谱对比可以发现，背景噪声的主要频谱范围和接收信号的主要频谱范围重叠部分很大，虽然有用信号的功率谱远大于噪声信号，但是由于探测目标体积较小、回波信号极小等原因，如果不对噪声进行去除，会严重减弱回波信号的信噪比，甚至接收不到回波信号。然而用经典频域滤波器却难以有效地去掉具有相同频率段的背景噪声。因此，需要采用小波变换的方法去除信号中的噪声干扰。