混沌随机系统的响应预测

沈焰焰

(福建船政交通职业学院,福建福州 350007)

其中,平均首尔穿越率定义为,

0 引 言

考虑到非线性动力学系统可能具有的复杂确定性响应以及随机响应,Y im等[1]和Naess等[2,5-7]建议利用随机响应的概率密度来分析混沌响应.事实上,在动力结构的工程分析中一个基本的响应预测就是估计相关响应变量的极值,对此,研究者通常是去估计它在一个特定时间范围内,超过某一个水平的可能性.基于此,本文主要利用路径积分法[2,5-7]来研究2种非线性动力系统的混沌响应,分别计算了高斯随机激励的混沌系统和l vy噪声激励的混沌系统的平均概率密度,讨论了高斯噪声和勒维噪声的首尔穿越率.

1 路径积分法原理

在文献[7]中,Naess介绍了Wehner等研究了借助路径积分法来寻求“非线性”FPK方程的形式解的思路,并首先提出求解较高维的FPK方程的路径积分数值方法.这里“非线性”指的是FPK方程漂移向量和扩散向量对系统状态变量的非线性依赖关系.研究人员之所以对形式解感兴趣,是因为路径积分能给出绕确定性路径的近似解的适当初值点.

路径积分的基本思想是,在空间和时间上分别离散化,以路径和代替积分,即通过连接短时的转移概率密度形成全局的转移概率密度,进而得到状态向量的联合概率密度函数.路径积分法最优越的特性在于可得到非负的、较准确的尾部概率密度.此外,路径积分法还可以计算系统的非平稳瞬态概率密度以及首次穿越问题等.

定义路径积分的最简便方法是把连续过程离散化在空间和时间限定的充分小的网格点上,然而,一个连续过程的离散化并不唯一.这样,对于不同的离散规则,就产生了许多不同的路径积分方法.为建立协变路径积分,就需要选择特定的离散化规则,这使得很多研究者致力于在不给出特定的离散化规则的情况下,提出各种推导佃变路径积分的方法.

2 两种混沌随机系统的平均概率密度

平均概率密度能很好地描述混沌吸引子.针对时变系统,特别是漂移或扩散系数中含有周期函数的系统,文献[3]引入时间上的平均概率密度定义:

2.1 高斯噪声的混沌运动

本研究在前人的工作基础上分析了复杂化的Van der Pol system混沌运动[3]:

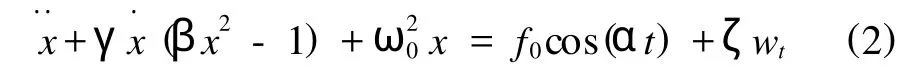
其中,γ、ζ都是正的,wt是标准的高斯白噪声,其强度为ζ,f0、α分别表示周期项系数的强度和频率.

当ζ=0时,式(2)就变成了确定性系统:

考虑式(2)在参数γ=2,β=1,ω20=1,f0= 0.3,α=1,ζ=0.005时,其时间平均的联合概率密度如图1所示.

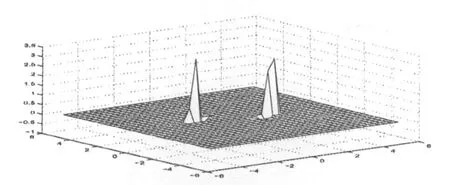
图1 特定参数下式(2)的时间平均的联合概率密度

由图1知,在随机激励较小时,随机系统的概率密度的形状在一定程度上可以表征相应的确定性系统的混沌吸引子结构,但当随机激励较大时,会使得确定性系统受到破坏.

2.2 l vy噪声的混沌运动

鉴于l vy过程越来越广泛地被应用在各相关领域,本研究尝试把高斯白噪声改成l vy噪声,l vy过程为α-stablel vy过程[4].考虑如下的动力系统:

其中,γ、ζ、β都是正的,Lt是α-stablel vy噪声,其强度为ζ,f0、α分别表示周期系数的强度和频率.

当ζ=0时,式(4)为确定性系统:

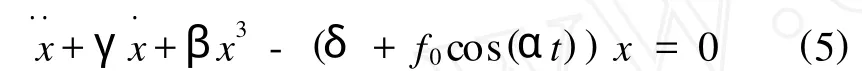
用路径积分方法求解式(4)在参数为,γ=0.3, β=1,δ=1,f0=0.6,α=1.2,ζ=0.0005时,其时间平均的联合概率密度分布如图2所示.

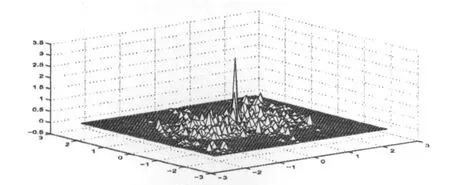
图2 特定参数下式(4)的时间平均的联合概率密度

3 混沌随机系统的响应预测

在动力结构的工程分析中一个基本的响应预测就是估计相关响应变量的极值,对此,研究者通常是去估计它在一个特定时间范围内,超过某一个水平的可能性.假设在有噪声激励的情况下,Yt=(Xt, X·t)的概率密度为,

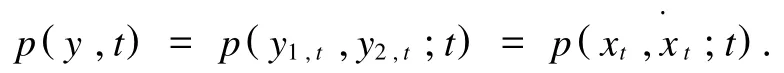
假设通过使用Rice公式可以计算水平为ζ的首尔穿越率.Rice公式如下,

实际估计 Xt的极值分布是依赖于高水平的首尔穿越事件是独立的这个前提假设.在给定一定的时间T内,就可以得到关于最大值X∧(T)=sup(Xt; 0≤t≤T)的分布函数,

因为转移概率密度函数是周期的,故当t′充分大,且 t>t′时,可以得到,

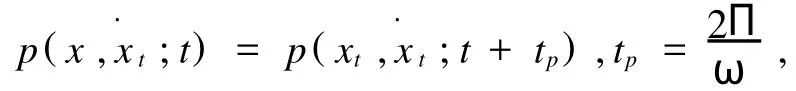
其中,ω为周期项系数的频率.设 T=mtp,则可得,

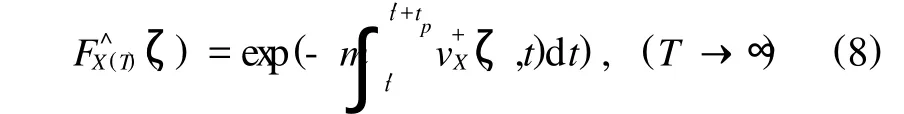
由平均概率密度可以导出,

这样,极值分布就可以改写成,

其中,平均首尔穿越率定义为,

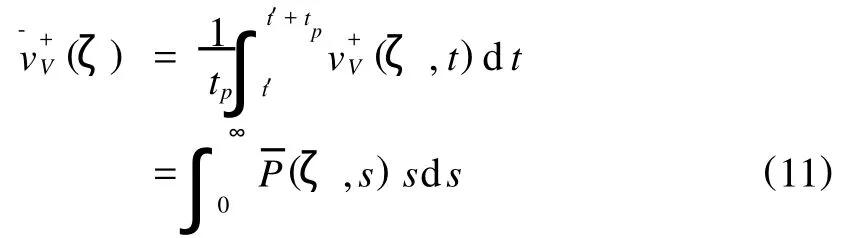
在这里,对于大的响应预测,平均概率密度是很重要的.式(2)、式(4)的首尔穿越率曲线如图3、图4所示.

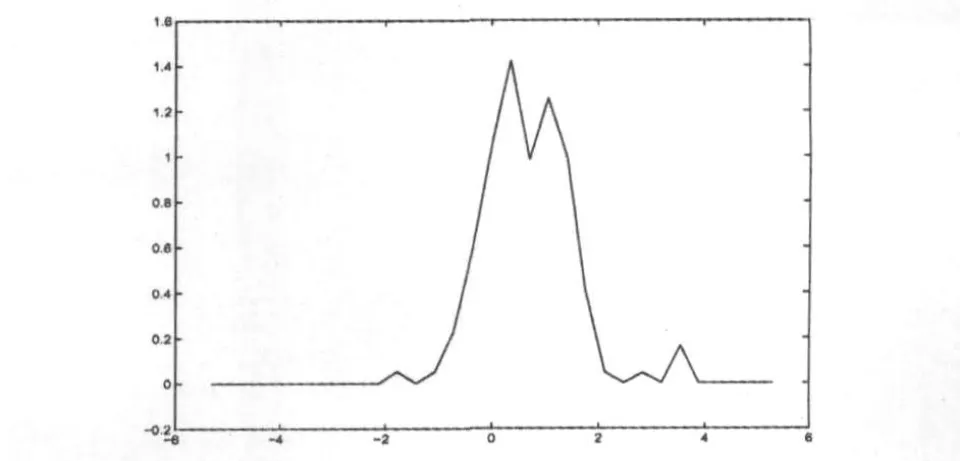
图3 式(2)的首尔穿越率曲线

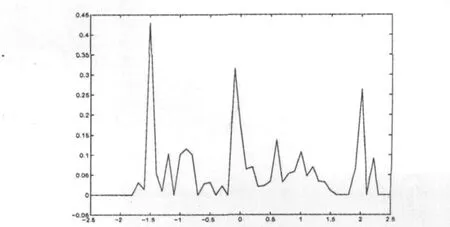
图4 式(4)的首尔穿越率曲线

4 结 论

本研究着重讨论了受高斯白噪声激励的混沌运动(2)在参数为γ=2,β=1,ω20=1,f0=0.3,α= 1,ζ=0.005下的平均概率密度、响应预测及首尔穿越率.本研究的另外一个重点就是尝试把高斯白噪声改成 l vy噪声,讨论了受 l vy噪声激励的混沌运动(4)在参数γ=0.3,β=1,δ=1,f0=0.6,α= 1.2,ζ=0.0005下的平均概率密度、响应预测及首尔穿越率.此外,还可以用概率密度角度解释混沌吸引子的存在性,即借助随机系统的概率密度在一定程度上刻画确定性系统的混沌吸引子.同时,通过实验发现,l vy噪声与高斯白噪声相比,其噪声强度要求相对更小,否则会使得确定系统遭到严重的破坏.

[1]Y im S C S,Lin H.Unified Analysis of Complex Nonlinear Motion Via Densities[J].Nonlinear Dynamics,2001,24(1):103-127.

[2]Naess A.Chaos and Nonlinear Stochastic Dynamics[J].Probalistic Engineering Mechanics,2000,15(1):37-47.

[3]Moon F C.Chaotic and Fractal Dynamics:An Intorduction for Applied Scientists and Engineers[M].New Y ork:Wilery-Interscience,1992.

[4]Samorodnitsky G,Taqqu M S.Stable Non-Gausian Random Processes[M].New Y ork:Chapman and Hall,1994.

[5]Naess A,JohnsenJ M.Response Statistics of Nonlinear Compliant Offshore Stuctures by the Path Integral Solution Method[J]. Probabilistic Engineering Mechanics,1993,8(2):91-106.

[6]Naess A,Moe V.Stationary and Non-stationary Radom Vibraton of Oscillators with Bilinear Hysteresis[J].International Journal of Non-Linear Mechanics,1996,31(5):553-562.

[7]Naess A,Moe V.Efficinet Path Integration Mehtod for Nonlinear Dynamic Systems[J].Probabilistic Engineering Mechanics, 2000,15(2):221-231.