带梯度项的半线性椭圆型方程正径向整大解的存在性＊

方钟波，茹海霞

（中国海洋大学数学科学学院，山东青岛266100）

0 引言

本文考虑带梯度项的半线性椭圆型方程

其中N≥3，m＞0，λ≠0，f（u）满足

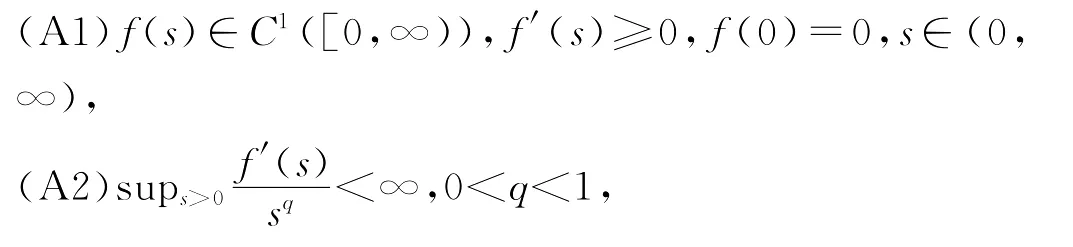
p（x）为非负连续函数，且有α＝infx∈RN p（x）＞0，β＝supx∈RNp（x）＞0。

对于方程（1），若当｜x｜→∞时，u（x）→∞，则称此时的解为整大解（Entire large solution）。

最近，关于有界区域中或整体空间中椭圆型方程大解的研究非常活跃，其中大解指的是当空间变量趋于边界时方程的解趋于无穷大。当Ω是RN空间中具有光滑边界的有界区域或整体空间且此时方程不带梯度项时，关于方程（1）的大解或整大解的存在性和非存在性的研究已得出很多结论。例如，Bieberbach［1］研究了p（x）＝1，f（u）＝eu的情形；高维情形中p（x）和f（u）满足适当条件时大解的存在性问题及爆破速率［2－3］；p（x）满足适当条件且f（u）为乘幂形式时整大解的存在性［4－6］等。当方程带有梯度项时，Lair和Shaker［7］利用单调收敛法证明了当p（x）满足适当条件且f（u）为乘幂形式时整大解存在性和不存在性的结论；在高维空间中p（x）满足衰退条件（当｜x｜→∞时，其中以及f（u）为满足过原点的正连续非减函数时整大解的存在性［8］。此外，当Ω是有界区域时Shuibo Huang和Qiaoyu Tian［9］利用上下解方法研究了大解的边界渐近性态。

1 主要结论

据查找文献所知，对拉普拉斯方程而言，p（x）满足较弱条件下的研究甚少。尤其是关于方程中梯度项的指数m＞0时正径向整大解存在性问题的研究还未展开。本文将采用Banach不动点定理和反证法证明正径向整大解的存在性。结果发现，正径向整大解的存在性依赖于梯度项的系数符号和指数的范围。详细结论如下：

定理1 若f满足（A1）和（A2），且λ＞0，m＞0或λ＜0，0＜m≤1则方程（1）存在正径向整大解u（r）。

2 主要结论的证明

为了证明定理，考虑如下更一般的径向问题

其中a＞0为常数。下面分3步来证明问题（2）～（4）存在正径向整大解。

第一步：局部存在性。

主要利用Banach不动点定理来证明问题（2）～（4）存在局部解。首先对方程（2）关于变量r从0到r积分，可得

考虑如下空间

其中ra，c为常数，

在空间E上定义映射T：

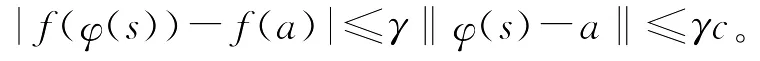
因为

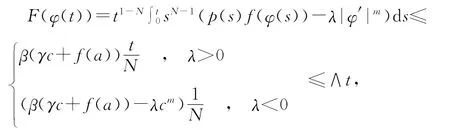
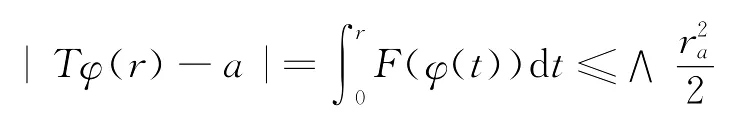
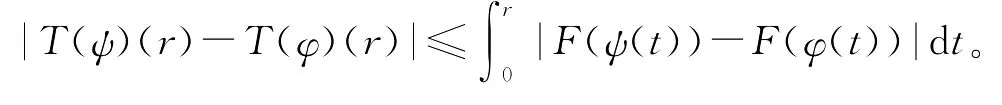
因为

所以有

同理可知

显然，若取ra≤inf（r1，r2，r3，r4），则T为压缩映射。由①②即得，问题（2）～（4）在［0，ra］内存在局部解。

第二步：整体存在性。

设问题（2）～（4）的解u＝u（·，a）的最大存在区间为［0，rmax），则只需验证rmax＝∞。

假设rmax＜∞，显然有u（r）→∞，当r→rmax。先把问题（2）～（4）转化为积分方程

上述积分方程中，若λ＞0，m＞0，则有

且

由条件（A2）知，当r→rmax时u（r）有界，这与假设矛盾。即rmax＝∞。

若λ＜0，0＜m≤1，则

即

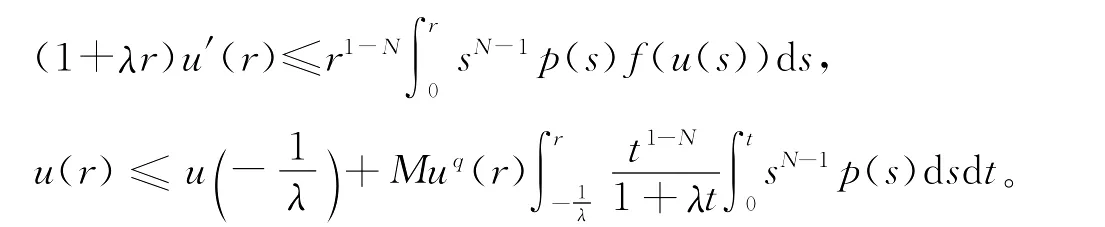
由条件（A2）知，当r→rmax时u（r）有界，这与假设矛盾。即rmax＝∞。

第三步：正径向解u（r）为整大解。

先证在［0，∞）上u′（r）≥0。由初值条件u（0）＝a和u（r）的连续性知，存在r0＞0，对任意的成立。又由条件（A1）知，对任意的有

即

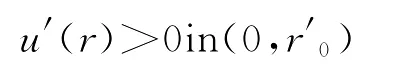
方程（2）两边取r→∞极限得

则存在充分大的r＞0，使得

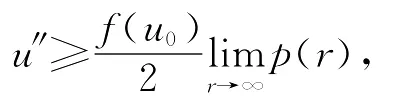
进而得

这与假设矛盾。

由上述1～3步知，方程（1）存在正径向整大解u（r）。

定理证毕。

［1］ Bieberbach L.Δu＝euund die automorphen Funktionen［J］.Math Ann，1916，77：173－212.

［2］ Lair A V.A necessary and sufficient condition for existence of large solutions to semilinear elliptic equations［J］.J Math Anal Appl，1999，240：205－218.

［3］ Zhang Zhijun，Ma Yunjie，Mi Ling，et al.Blow－up rates of large solutions for elliptic equations［J］.J Differ Equations，2010，249：180－199.

［4］ Lair A V，Wood A W.Large solutions of sublinear elliptic equations［J］.Nonlinear Anal，2000，39：745－753.

［5］ Cheng K S，Ni W M.On the structure of the conformal scalar curvature equation on RN［J］.Indiana Univ Math J，1992，41：261－278.

［6］ Tao Shuangping，Zhang Zhijun.On the existence of explosive solutions for semilinear elliptic problem［J］.Nonlinear Anal，2002，48：1043－1050.

［7］ Lair A V，Shaker A W.Large solutions of semilinear elliptic equations with nonlinear gradient terms［J］.Int J Math Sci，1999，22：869－883.

［8］ Peng Yahong，Wang Yaguang.Large solution of a semilinear elliptic problem［J］.Comput Math Appl，2005，49：1387－1395.

［9］ Huang Shuibo，Tian Qiaoyu.Asymptotic behavior of large solution for boundary blowup problems with nonlinear gradient terms［J］.Appl Math Comput，2009，215：3091－3097.