太湖风浪场的计算与比较

张洪生，戴 甦，张 怡

(1.上海海事大学海洋环境与工程学院，上海 201306;2.水利部太湖流域管理局，上海 200434)

太湖风浪场的计算与比较

张洪生1，戴 甦2，张 怡2

(1.上海海事大学海洋环境与工程学院，上海 201306;2.水利部太湖流域管理局，上海 200434)

首先探讨了浅水风浪数值模型—SWAN模型应用于模拟内陆湖泊风浪生成和传播变形时的特点。该模型存在不能有效地模拟近固壁边界处风浪场的缺点，以能正确地模拟湖区的风浪场和节约计算时间为原则，确定了计算范围。对太湖进行了风场和风浪场的现场观测。分别利用规范公式和SWAN模型两种方法、根据观测和预报的风场计算了湖区的有效波高，并将计算结果和现场观测值进行了详细比较。结果表明基于观测的风场，利用两种方法所计算的太湖风浪场的精度基本相当;在根据观测的风场、利用SWAN模型计算内陆湖泊的风浪场时，需要精心选择恰当的风场;在根据预报的风场预报湖区风浪场时，SWAN模型的精度要高于规范公式的精度。

风浪场;风场;SWAN模型;规范公式;太湖

作为太湖流域第一大湖的太湖，是长江中下游五大淡水湖之一。湖面形态如向西突出的新月。湖区南岸为典型的圆弧形岸线，东北岸曲折多湾，湖岬、湖荡相间分布，以湖岸计算的湖泊面积为2 427.8 km2。太湖中现有51个岛屿，总面积为89.7 km2。因此，太湖实际水面面积为2 338.1 km2。岸线总长为405 km，平均水深为1.89 m，为平原浅水湖泊，具有风生浪起的特征。太湖流域属亚热带季风气候区。冬季受大陆冷气团侵袭，盛行偏北风;夏季受海洋气团的控制，盛行东南风，水汽丰沛。夏秋季节在东南季风的影响下，降水量大，导致水位暴涨［1］。大风尤其是台风天气，又会导致风浪的增大，而风浪可导致堤坝工程护坡的损坏和淘刷。因而研究太湖水域的风浪对环湖大提工程的建设、维护和防汛都具有十分重要的意义。

计算内陆湖泊的风浪场可以采用两种方法:一种是经验公式的方法，例如，《堤防工程设计规范》(GB50286-98)［2］规定的方法;另一种是采用风浪数值模型进行模拟的方法。文献［2］规定了计算内陆湖泊风浪要素的方法。该方法在计算单个工程位置的波要素时较为简单，但采用该方法很难较快地计算出整个湖区在不同时刻的波要素。Simulating Waves Nearshore(简写为SWAN)模型［3］是荷兰Delft理工大学基于第三代风浪模式而建立的风浪数值模型，该模型综合考虑了波浪传播过程中水底地形的折射影响、波浪破碎、底摩擦、波波相互作用和白帽浪等多种因素的影响，是国际上比较通用的近岸风浪模型［4-6］。应用该模型可以得到在计算的有效时间段内的任意时刻在任意位置上的波要素。根据实测的风场和风浪场，文献［5］验证了它应用于河口海岸地区时的精度;根据计算的风场，文献［7］将计算的风浪场和实测值进行了比较。现在该模型仍处于不断发展和完善之中［8-9］。近年来，有部分学者将该模型应用于内陆湖泊风浪场的数值模拟［10-11］。相对于近岸水域，一般说来内陆湖泊的岸线更为曲折复杂，水深变化也更为剧烈。这就需要探讨如何将该模型应用于内陆湖泊风浪的数值模拟。而且，SWAN模型和规范公式两种方法的计算精度，需要进行详细的比较。文献［12］根据两天观测的风场和风浪场，在淀山湖水域初步地比较了SWAN模型和规范公式的计算精度，但淀山湖水域面积狭小，仅63 km2。

首先探讨了风速和水深定常情况下，利用SWAN模型模拟侧边界为固壁边界的计算域内波高随空间变化的特点，以此确定合适的计算范围。然后将分别利用规范公式和SWAN模型两种方法，根据多天观测和预报的风场进行计算所得的波高与现场观测值进行了详细比较，从而研究了两种计算方法的精度。

1 SWAN模型的简介与测试

1.1 模型的简介

SWAN模型［3］是根据风、底部和水流的条件对近海地区、湖泊和河口的波浪参数进行现实模拟的第三代波浪模型。该模型的控制方程是基于带有源汇项的波作用平衡方程，其在直角坐标系下的表达形式:

式中:N(σ，θ)=E(σ，θ)/σ，σ 为相对频率，θ为波向，E(σ，θ)为能谱密度，N(σ，θ)为波作用量;cx，cy，cσ和cθ分别为波作用量在x方向、y方向、频率空间和波向空间中的传播速度;S代表各物理过程所产生的源汇项。

模型的优点是能够根据需要灵活选用所需要考虑的物理过程以及某一物理过程的不同参数化形式。模型采用全隐式有限差分格式求解，无条件稳定，与采用显式有限差分格式的传统波浪谱模型相比，其时间步长可以取得更大，在用作波浪预报时增强了其时效性。

1.2 模型有关参数的选取

SWAN模型中包含有若干物理过程的处理，相应地含有不少计算参数。但模型手册［3］强烈建议使用模型系数的缺省值。鉴于该模型是一个得到较为广泛使用的模型，在数值计算太湖的风浪场时，对于物理过程的处理我们使用了SWAN模型建议的相关参数值。其它相关参数主要有:θ空间的网格数采用36，即谱方向的分辨率为 10°;最小频率为 0.08 Hz、最高频率为 1.0 Hz。JONSWAP底摩擦公式的系数取为0.067 m2/s3。当波高的最大值与水深的比值为0.73时允许波浪破碎。数值求解格式采用一阶的空间和时间向后差分格式(BSBT)。

1.3 计算范围的测试

鉴于内陆湖泊的边界大多为固壁边界，因此，假设计算域的侧边界为固壁边界，以此探讨固壁边界对模型计算结果的影响。

假定水深和风速定常，以检验在理想状态下SWAN模型计算结果的特点。采用恒稳模式(stationary mode)进行计算。淀山湖五十年一遇的设计风速为20.3 m/s［13］。淀山湖和太湖同属太湖流域，因此假定10 m高度处的风速为20.0 m/s，这一风速属8级风。假设计算域的水深为1 000.0 m。计算域沿x和y轴方向的长度分别为15和60 km，y方向计算域的两端均为固壁边界，x轴设在计算域的中心，并假定风向沿x轴。计算网格点为151×601，x和y方向的网格空间步长均为100 m。

计算结果见图1和2。在图1中，横坐标为无因次化的风距，纵坐标为无因次化的有效波高，它们的表达式分别为

式中:X为风距，单位为m;g为重力加速度，单位为m/s2;H为有效波高，单位为m;U10为10 m高度处的风速，单位为m/s;˜X为无因次化的风距;˜H为无因次化的有效波高。

由图1和2可见，波高关于x轴对称，而且在距离侧边界约15 km范围内所计算的波高失真;出流边界对波高计算结果无影响。

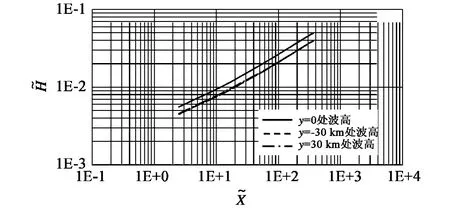
图1 沿风向的波高沿程变化Fig.1 The spatial distribution of calculated wave heights along the wind direction

图2 与风向垂直方向的波高沿程变化Fig.2 The spatial distribution of calculated wave heights across the wind direction

进一步检验模型在水深较浅情况下的计算结果。将水深设为3 m，计算范围为70 km×120 km，10 m高度处的风速仍为20.0 m/s。计算网格为351×201，x和y方向的网格空间步长均为200 m。

计算结果见图3。由图3可见，在x=35.0 km和x=70.0 km处的波高一致，这是因为风距足够大。但仍在侧边界的一定距离内所计算的波高失效，此距离为2 km。对比图2和3可见，随水深的变小，计算结果失真的范围也变小。

鉴于水深的大小影响到计算结果的有效范围，参照太湖最高水位和最低水位来探讨模式的计算结果的特点。将计算域设为90 km×90 km，风速仍设为20 m/s，参照多年平均值，将最高和最低水位分别设为4.97和1.78 m(吴淞高程)。根据太湖的水深地形图，分别对应于最高和最低水位，将水深分别设为4.5和1.24 m。

水深为4.5 m时的计算结果见图4和5;水深为1.24 m时的计算结果见图6。对比最高和最低水位的计算结果，仍可明显地看出水深越浅，计算结果的失真范围越小。在多年平均的最高水位时，在距离侧边界9 km左右的范围内计算结果失真;在多年平均最低水位时，在距离侧边界约2 km的范围计算结果失真。这两组计算结果为确定太湖的有效计算区域提供了非常有力的支持。

图3 与风向垂直方向的波高沿程变化Fig.3 The spatial distribution of calculated wave heights across the wind direction

图4 沿风向的波高沿程变化Fig.4 The spatial distribution of calculated wave heights along the wind direction

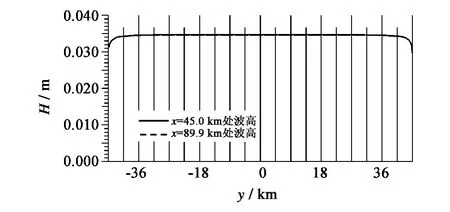
图5 与风向垂直方向的波高沿程变化(水深4.5 m)Fig.5 The spatial distribution of calculated wave heights across the wind direction

图6 与风向垂直方向的波高沿程变化(水深1.24 m)Fig.6 The spatial distribution of calculated wave heights across the wind direction

综上所述，SWAN模型数值解的有效范围随水深的变化而变化:水深越大，计算结果的失真范围越大;水深越小，计算结果的失真范围越小。对于太湖这一实际地形，需要适当地扩大其计算范围。遵循的原则是:既尽可能地使整个实际水域都在有效计算范围内，又不过大地扩大计算范围，以避免过多地增加计算时间。

2 现场观测的介绍

2.1 观测位置

在三个测点位置进行了风场和风浪场的现场测量，其中1号站位(大浦口站)的坐标为(东经119.931 19°、北纬31.266 06°)，2 号站位(贡湖站)的坐标为(东径120.395 94°、北纬31.443 89°)，3 号站位(平台山站)的坐标为(东经120.105 6°、北纬30.231 8°)。三个站位的示意见图7。

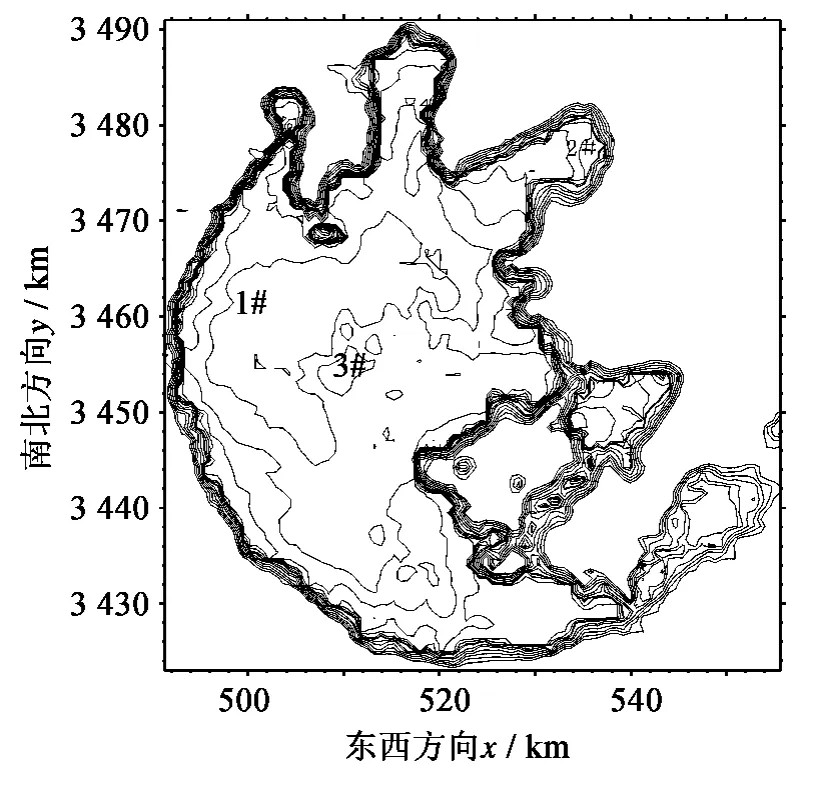
图7 各测站位置示意Fig.7 The sketch of measurement locations of Taihu Lake

2.2 观测结果

由于湖中三个观测站处于运行的初期，观测部门在采集观测数据时还缺乏比较完善的手段，因此，观测数据［14］并不连续。而且观测的波高部分偏离正常值，主要是偏大。例如，2号站─贡湖站从8月21日20时到22日20时的波浪观测资料存在明显问题，其25个整点时刻的有效波高记录值分别为:1.529、0.968、0.16、0.134、0.364、1.1、无数据、0.798、5.496、3.968、2.242、0.18、0.669、0.159、0.132、0.131、0.157、0.195、0.311、0.67、0.162、1.513、0.119、1.038 和1.118 m。太湖是一个水深很浅的内陆湖泊，而贡湖站在离岸不远的湖湾内，根本不可能在该站产生太大的波高。在上述时段内三个观测站风速观测值的平均值在5 m/s左右，并且大部分时间的风向在东到东东南之间，该风向对贡湖站来说属离岸风。但在上述时段内相当一部分记录的有效波高却达0.5 m以上，甚至有3.968 m和5.496 m的记录值，显然观测结果存在问题。判断某一观测站记录的波高值是否正常的根据是:和前后时段的波高观测值相比较是否存在明显偏差(主要是偏大);如果存在明显偏差，则进一步观察在该时段前后的风场有无明显变化、与其他两个观测站的波高观测值相比有无异常。如观测数据存在较为明显的问题，在进行统计计算时，将不对该数据进行统计。对于“存在较为明显的问题”的数据的选择，采取了非常慎重的态度，而不会采用实用主义的态度。鉴于风浪对太湖的危害主要是发生在秋季，因此，计算2007年8月8日到9月2日期间的风浪场。在此期间，台风“圣帕”影响太湖流域。在选取有效的观测天数时，要兼顾到第4节提到的预报情况，即如果某一天只有观测的风场和风浪场，而无预报的风场资料，那么也没有统计该天的观测资料。为了便于和预报的风场，及据此计算的风浪场相比较，这里“某一天”的含义是从当日20时开始，到第二天19时结束。选取了2007年8月8日到9月2日期间的20天。有效的观测结果见表1。在表1中，为了便于比较各测站的观测值，选取了三个站都有有效的观测值的时刻进行统计。

在表1中，为了便于比较各站观测风速的大小，采用式(3)将各站的观测值统一换算为10米高度处的风速值U［15］:

式中:Up为各观测站的风速观测值;h=10 m;h0=0.03 m;hp为各观测站的位置高度(m)。

湖中的大浦口和平台山站的风力风向仪安装高程为15.08 m，在太湖平均水位(以3.00 m计)以上12.08 m，湖中的贡湖站的风力风向仪安装高程为23.00 m，在太湖平均水位以上20.00 m。因此，对于1号和3号站，hp=12.08 m;对应于2号站，hp=20.00 m。

由表1可见，紧靠岸边的2号站的风速最小，分别比水面开阔处的1号和3号站的风速小1.76 m/s和2.08 m/s。尽管在8月21日2号站没有有效的观测波高，但为了尽可能多地利用观测资料，仍统计了该日1号和3号站的有效波高。在19天中(不包括21号的观测结果)，1号、2号和3号站的平均有效波高分别为0.34 m、0.15 m和0.37 m。和风场类似，离岸最近的2号站的波高最小，分别为1号站和3号站波高的44.12%和40.54%。虽然2号站距离岸边较近，其离岸的最小距离也有2.0 km左右，但观测到的最大有效波高也还远未达到破碎的标准。

表1 各观测站的风场和风浪场统计表Tab.1 The statistical table of the measured wind fields and wind wave fields at different locations

3 根据观测风速所计算的波高的比较

3.1 利用规范公式计算波高

文献［2］规定了计算内陆湖泊风浪要素的方法。鉴于太湖水域的边界形状很不规则，需要引入等效风区长度的概念来进行波浪的计算。等效风区长度Fe的计算公式:

式中:ri为主风向两侧各45°范围内，每隔Δα角由计算点引到对岸的射线长度(m);αi为射线ri与主风向上射线 r0之间的夹角(°)，αi=i×Δα，可取 Δα =15°，i=0，±1，±2，±3。见图8。

太湖两岸之间的最大长度均不超过100.0 km，因此可不计入风时的影响。应用式(5)计算平均波高:

3.2 利用SWAN模型计算波高

3.2.1 计算范围的选取及水深的插值

整个 太 湖 水 域 在 (119°53'00″，30°55'00″)(西 南 角)、(119°53'00″，31°34'00″)(西 北 角)、(120°40’00”，31°34’00”)(东北角)和(120°40'00″，30°55'00″)(东南角)的矩形范围内，见图 7。正如在 1.3所讨论的，SWAN模型不能有效地模拟近边界处的浪高，因此，需要适当扩大计算范围。鉴于太湖的防汛工作所关心的重点是西大堤，同时考虑到南、北方向水域开阔以及东太湖的实际有价值的计算范围比较狭小，将水域的最外侧向西延伸12.8 km、向东延伸2.5 km，向南延伸14.9 km，向北延伸13.0 km。延长后的计算域大小为南北长为100.0 km，东西长为90.0 km。在平面直角坐标系中进行计算。延长后的计算域四个角点分别为(119°44'57.382 68″，30°46'58.688 23″)(西南角)、(119°44'48.767 43″，31°41'05.543 35″)(西北角)、(120°41'45.821 14″，31°40'59.610 92″)(东北角)和(120°41'22.131 83″，30°46'52.961 66″)(东南角)。扩展后的计算域范围见图9。

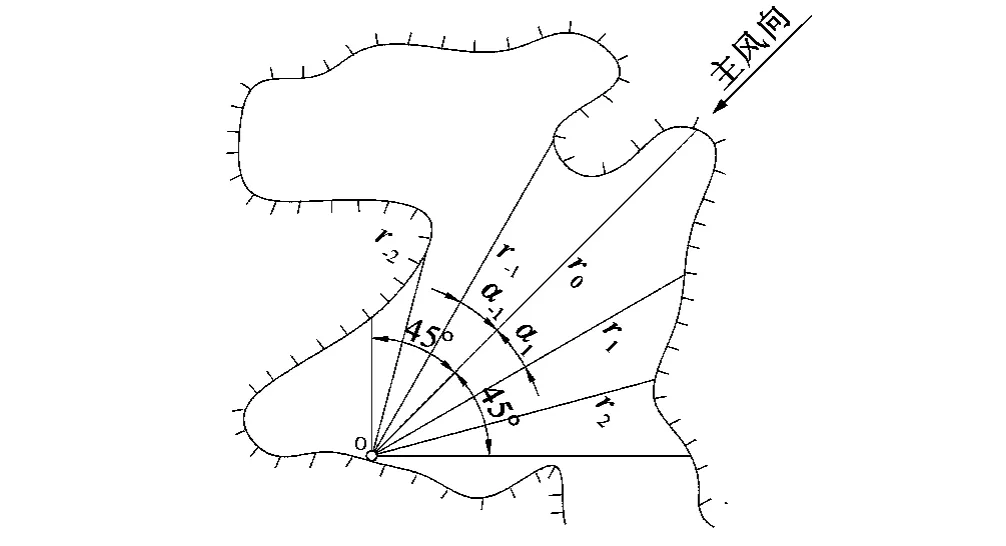
图8 等效风区长度计算Fig.8 The calculation chart of equivalent fetch length

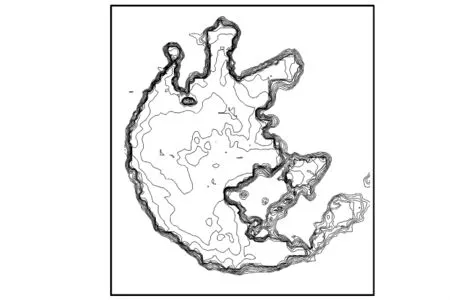
图9 扩展后的太湖水域计算范围示意Fig.9 The sketch of extended calculation domain of Taihu Lake

3.2.2 水深的插值计算风场的选取

经过数值试验，将计算域剖分为200×200个网格，在x(东西方向)和y方向(南北方向)的网格步长分别为450 m和500 m。将读入点的水底地形高程插值到计算网格点上。采用如下公式进行插值:

其中，Sj为第j个节点到第i点的距离，ωj为权重。水位减去水底地形高程即为水深。

如表1所示，湖区三个观测站的风速和浪高都存在差别，特别是靠近岸边的2号站的风速和浪高均明显小于其它两站。在利用SWAN模型进行计算时，首先用三站平均的风场作为输入，然后再用1号站和3号站平均的风场作为输入，输出3个站位的浪高;最后用2号站的风场作为输入，单独输出2号站的浪高。以此和经验公式的计算值以及观测值进行比较。

3.2.3 不同计算结果的比较

计算结果见表2～4。在表2～4中，“有效时刻”的含义是指既有有效的波高观测值，SWAN模型的计算结果也可以接受(计算结果稳定)，还可以利用经验公式得到波高计算结果的时刻。例如，在8月8日的20时和21时两个时刻，虽然可以利用SWAN模型进行计算，但这两个时刻的风浪还不稳定，因此，将这两个时刻作为无效时刻。表中，H0代表观测的有效波高(m);Hcm代表利用规范公式计算所得的有效波高(m);Hcs3代表利用SWAN模型，根据三个站点的平均风场计算所得的有效波高(m);Hcs2代表利用SWAN模型，根据1号和3号站点的平均风场计算所得的有效波高(m);Hcs1代表利用SWAN模型，根据单站点的风场计算所得的有效波高(m)(文中仅根据2号站的风场输出了该站的波高)。由于各天的有效时刻数不同，在计算平均的绝对误差和分散系数SI(Scatter Index)［16］时，是对所有的有效时刻的数据进行统一计算，而非简单的算术平均。分散系数的计算表达式为:

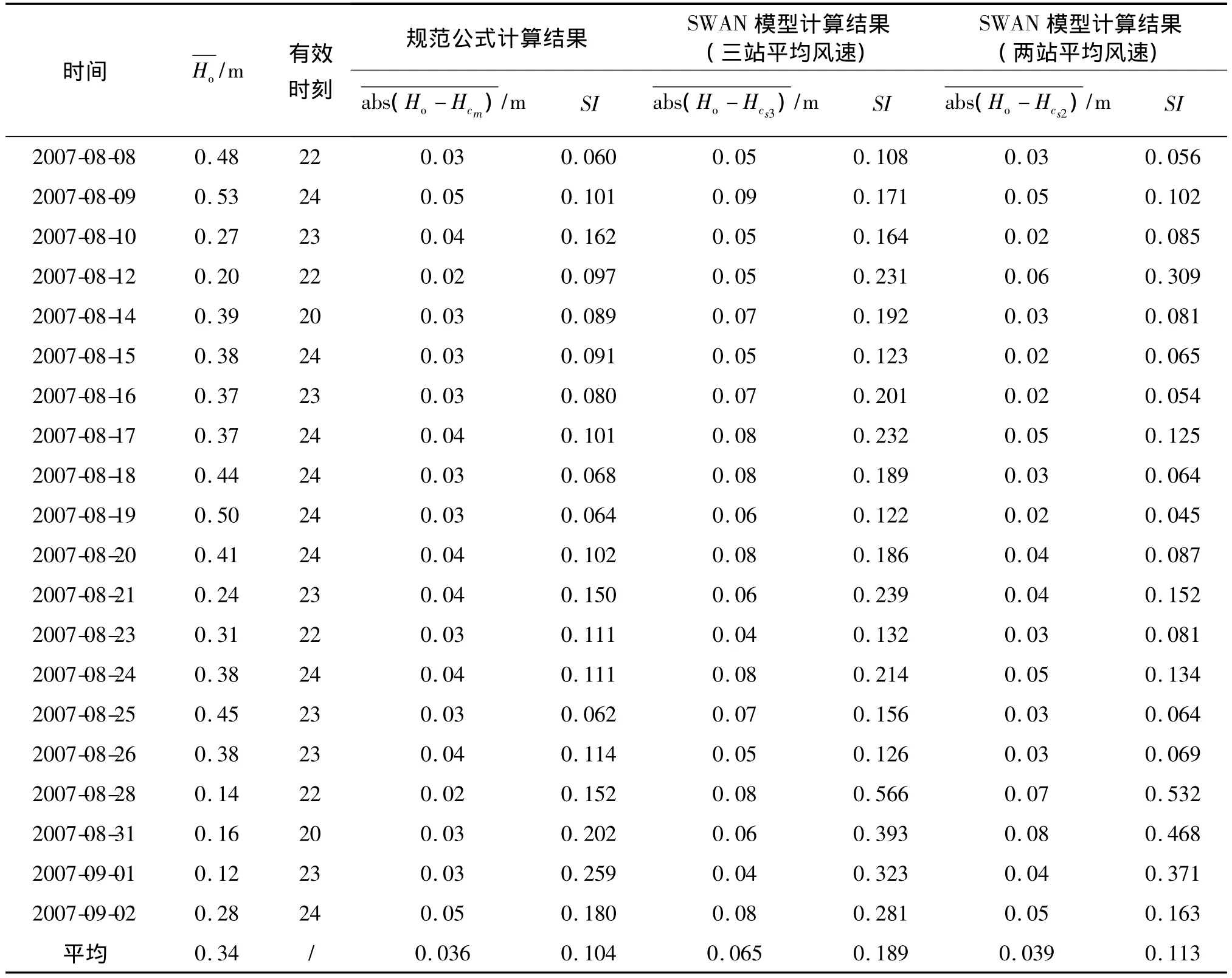
表2 1号站位的波高结果比较表Tab.2 The comparisons between the measured and calculated wave heights at location 1

在计算所有时刻的绝对误差的平均值时，为了更好地判断利用不同方法所得计算结果的精度，在小数点后保留了三位有效数字。由表2可见，1号站在有效时刻内的观测的有效波高的平均值为0.34 m;利用规范公式进行计算，所得结果的精度最高，平均绝对误差为0.036 m，SI为0.104;根据两站平均风速，即1号站和3号站的平均风速、利用SWAN模型进行计算，所得结果的精度次之，平均绝对误差为0.039 m，SI为0.113;根据三站平均风速、利用SWAN模型进行计算，所得结果的精度最低，绝对误差为0.065 m，SI为0.189。由表3可见，2号站在有效时刻内的观测的有效波高的平均值为0.16 m;利用规范公式进行计算，所得结果的精度最高，平均绝对误差0.048 m，SI为0.296;单独根据该站风速、利用SWAN模型进行计算，所得结果的精度次之，平均绝对误差为0.049 m，SI为0.305;根据三站平均风速，利用SWAN模型进行计算，所得结果的精度排在第三位，平均绝对误差为0.072 m，SI为0.442;根据1号站和3号站两个站的平均风速，利用SWAN模型进行计算，所得结果的精度最低，绝对误差为0.087 m，SI为0.540。由表4可见，3号站在有效时刻内的观测的有效波高的平均值为0.37 m;根据1号站和3号站两个站的平均风速，利用SWAN模型进行计算，所得计算结果的精度最高，绝对误差为0.041 m，SI为0.111;利用规范公式进行计算，所得结果的精度次之，绝对误差0.045 m，SI为0.120;根据三站平均风速，利用SWAN模型进行计算，所得结果的精度最低，绝对误差为 0.064 m，SI为0.172。

表3 2号站位的波高结果比较表Tab.3 The comparisons between the measured and calculated wave heights at location 2

如前所述，2号站位距离岸边很近，其风速和波高均比其它两个站位为小。因此，当利用SWAN模型计算该站的风浪场时，如根据三站平均的风场进行计算，误差明显偏大;如根据1号和3号两站的平均风场进行计算，则计算结果的误差就更大了。如仅仅将该站的风速作为输入，那么利用SWAN模型进行计算所得结果的精度和利用经验公式进行计算所得结果的精度相当。鉴于1号站和3号站都处于水域开阔处，将两个站的计算结果进行算术平均:在利用经验公式进行计算时，两个站的平均绝对误差为0.040 m，SI为0.112;在利用SWAN模型、根据三站平均风速进行计算时，两个站的平均绝对误差为0.064 m，SI为0.181;在利用SWAN模型、根据两站平均风速进行计算时，两个站的平均绝对误差为0.040 m，SI为0.112。可见，利用SWAN模型、根据两站平均风速进行计算所得结果的精度与经验公式所得结果的精度相当。如果根据三站平均风场、利用SWAN模型计算1号和3号站这两个站点的风浪场，那么计算精度明显偏低。其原因仍然是2号站的风速明显小于这两个站的风速。因此，在利用SWAN模型、根据实测的风速计算内陆湖泊的风浪场时，恰当地选择观测站点，进而正确地输入风场至关重要;在选择恰当风场的情况下，利用SWAN模型进行计算所得结果的精度与经验公式的精度相当。

表4 3号站位的波高结果比较表Tab.4 The comparisons between the measured and calculated wave heights at location 3

将各时刻的观测值(Ho)减去计算值(Hc)，对计算的差值的正负情况进行分析，结果见表5。1号站位总共比较了458个时刻，184个时刻的Ho大于等于Hcm，274个时刻的Ho小于Hcm;340个时刻的Ho大于等于Hcs3，118个时刻的Ho小于Hcs3;269个时刻的Ho大于等于Hcs2，189个时刻的Ho小于Hcs2。3号站位总共比较了420个时刻，240个时刻的Ho大于等于Hcm，180个时刻的Ho小于Hcm;358个时刻的Ho大于等于Hcs3，62个时刻的Ho小于Hcs3;304个时刻的Ho大于等于Hcs2，116个时刻的Ho小于Hcs2。可见，在利用SWAN模型计算1号和3号站的波高时，如根据三个站点的平均风速进行计算，则所得结果明显偏小;恰当的方法是以这两个站的平均风速作为输入。2号站位总共比较了358个时刻，280个时刻的Ho大于等于Hcm，78个时刻的Ho小于Hcm;109个时刻的Ho大于等于Hcs3，249个时刻的Ho小于Hcs3;98个时刻的Ho大于等于Hcs2，260个时刻的Ho小于Hcs2;152个时刻的Ho大于等于Hcs1，204个时刻的Ho小于Hcs1(考虑到风浪场的稳定性，少统计了两个时刻)。从这个统计结果也可看出，对于2号站，单独利用该站的风场作为输入，进行风浪数值模型的计算更为合理。

表5 各站位的观测波高与计算波高相比大小情况Tab.5 The variations of sign for the measured wave heights in contrast to the calculated ones at different locations

为了进一步定量地探讨利用不同方法所得计算结果的精度，采用公式［17］:

进行定量地比较。其中，x(j)为标准值(这里为现场观测值)，¯x为x(j)的平均值，y(j)为计算值。当d=0时代表二者完全失配;当d=1时代表二者完全一致。

利用不同方法所得计算结果与现场观测值的一致程度比较见表6。根据经验公式的计算结果统计的1号站和3号站的d的平均值为0.952;以三站平均风速作为输入、根据SWAN模型的数值解统计的1号站和3号站的d的平均值为0.894;以1号和3号站的平均风速作为输入、根据SWAN模型的数值解统计的这两个站位的d的平均值为0.953。由此可见，经验公式的计算结果和以两站平均风速作为输入、利用SWAN模型进行计算所得结果的精度相当;以三站平均风速作为输入、利用SWAN模型进行计算所得结果的精度仍然稍低。对2号站而言，利用经验公式进行计算所得结果的精度最高;在利用SWAN模型进行计算时，以该站的风场作为输入所得结果的精度最高，以三站平均风速作为输入所得结果的精度次之，以1号和3号站的平均风速作为输入所得结果的精度最低。从一致程度的定量比较，也可看出前述结论是正确的。

表6 以现场观测值作为x(j)、以不同方法的计算结果作为y(j)计算的dTab.6 The calculated index d with field data as x(j)and calculated results as y(j)

4 根据预报风场所计算的波高的比较

4.1 风场预报结果的简介

为了能够预报太湖的风浪场，采用上海市气象局建立的上海短时数值天气预报模式所模拟计算的风场，上海市据此发布每日的天气预报。该模式是以美国新一代中尺度数值预报业务和研究模式—WRF(Weather Research and Forecasting model)模式［18］的三重嵌套为框架进行研究开发的。该模式覆盖了太湖水域。采用每天20时开始起报、网格步长为3 km×3 km、时间步长为2小时的风场数据，该数据提供13个时次(20、22、00、02、04、06、08、10、12、14、16、18 和 20 时)的风场。所提供的风场计算结果都是固定的数据格式，通过编写程序读取风场，将风场插值到计算点上。插值方法同对水深的处理。

三个站位既有风场观测值又有风场预报值的时刻总共200个。在统计的所有时刻内1号、2号和3号站位的风速与风向的平均绝对误差分别为1.64、1.37 和3.32 m/s，30.67°、21.92°和32.50°。三个站位的平均风速和风向误差分别为2.11 m/s和28.36°。观测风场和预报风场的详细比较情况可参见文献［14］。因此，预报风场的误差在可以接受的范围内。

4.2 根据预报风场利用不同方法计算的波高的比较

计算结果见表7～9。在表中，“有效时刻”的含义同样是指既有有效的波高观测值，SWAN模型的计算结果也可以接受采用，还可以利用经验公式得到波高计算结果的时刻;Hcs为利用SWAN模型计算的有效波高(m)。由于各天的有效时刻数不同，在计算平均的绝对误差和SI时，同样是对所有的有效时刻的数据进行统一计算，而非简单的算术平均。

表7 1号站位的波高结果比较表Tab.7 The comparisons between the measured and calculated wave heights at location 1

表8 2号站位的波高结果比较表Tab.8 The comparisons between the measured and calculated wave heights at location 2

续表8

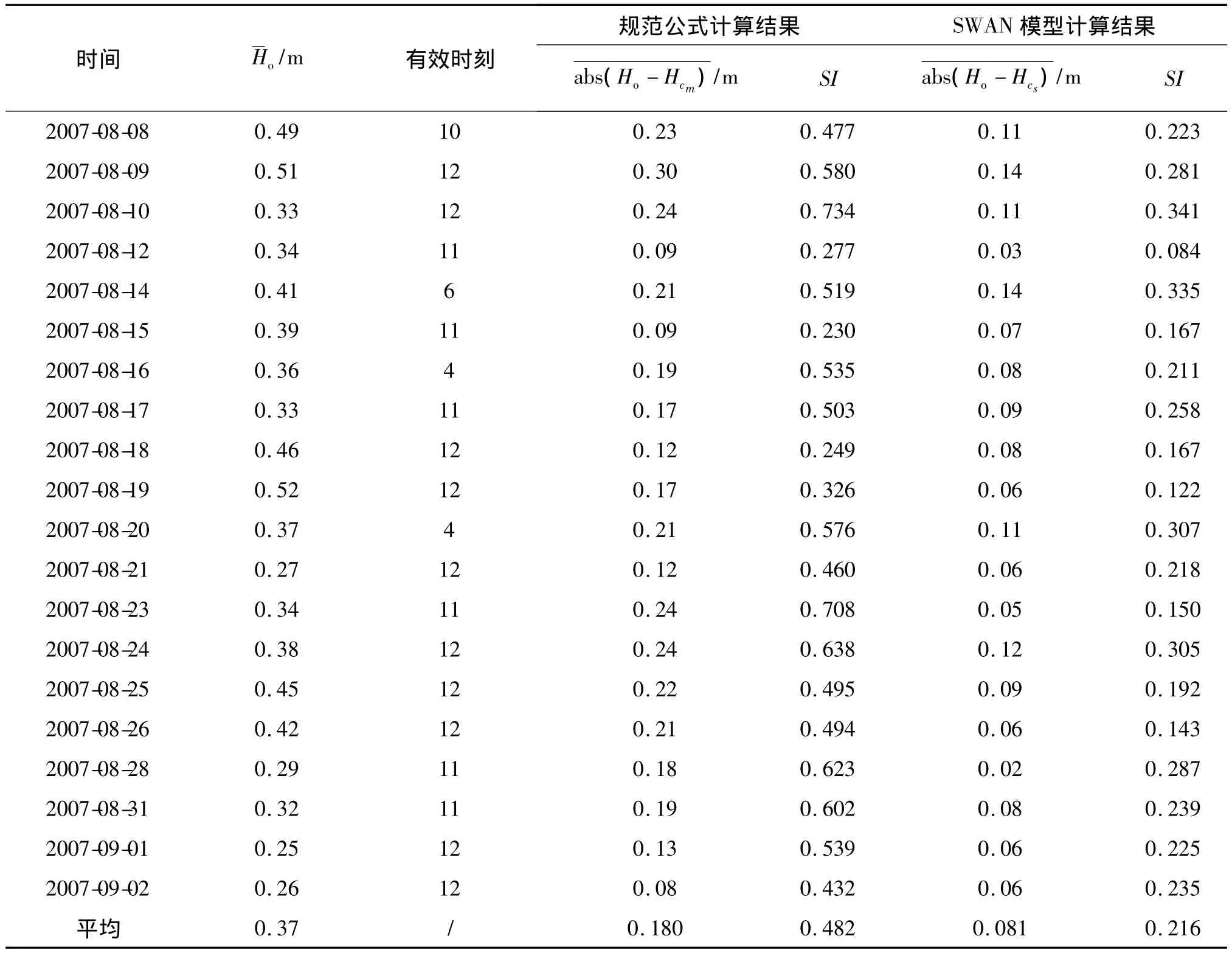
表9 3号站位的波高结果比较表Tab.9 The comparisons between the measured and calculated wave heights at location 3

由表7可见，1号站在有效时刻内的观测的有效波高的平均值为0.34 m;利用规范公式进行计算，所得结果的精度较高，平均绝对误差为0.078 m，SI为0.227;利用SWAN模型进行计算所得结果的精度较低，绝对误差为0.084 m，SI为0.245。由表8可见，2号站在有效时刻内的观测的有效波高的平均值为0.16 m;利用规范公式进行计算所得结果的精度较低，绝对误差为0.072 m，SI为0.439;利用SWAN模型进行计算所得结果的精度较高，绝对误差为0.053 m，SI为0.322。由表9可见，3号站在有效时刻内的观测的有效波高的平均值为0.37 m;利用规范公式进行计算所得结果的精度较低，绝对误差0.180 m，SI为0.482;利用SWAN模型进行计算所得计算结果的精度较高，绝对误差为0.081 m，SI为0.216。3号站位利用规范公式所计算的波高误差较大，其原因应当是该站的风场误差较大、而规范公式计算波高的方法是直接利用该站的风场进行计算。对三个站位的计算结果进行算术平均:利用规范公式和利用SWAN模型进行计算的平均绝对误差分别为0.110 m和0.072 m;SI分别为0.383和0.261。因此，当利用预报风速预报风浪场时，SWAN模型的精度明显高于规范公式的精度。其原因应当是预报的风场存在一定的误差，而规范公式是利用单个站点的风场进行计算，这样就会导致利用该方法进行计算所得结果的精度较低;而SWAN模型则是全区域进行连立求解，会部分地减少在部分站点较大的风速误差所引起的风浪场的误差。而文献［5］根据实测的风场、在平均波高为0.99 m时，利用SWAN模型的恒稳模式计算的河口海岸地区的风浪场的绝对误差为0.15 m，SI为0.37;文献［16］根据实测的风场，在平均波高为0.81 m时，利用SWAN模型的非恒稳模式计算的内陆湖泊的风浪场的SI为0.19。因此，根据预报的风场，计算风浪场是可行的。

利用不同方法所得计算结果与现场观测值的一致程度比较见表10。根据经验公式的计算结果统计的d的平均值为0.638;根据SWAN模型的数值解统计的d的平均值为0.712。从表10也可看出，SWAN模型的计算精度要高于规范公式的计算精度。

表10 以现场观测值作为x(j)、以不同方法的计算结果作为y(j)计算的dTab.10 The calculated index d with field data as x(j)and calculated results as y(j)

5 结语

1)首先探讨了浅水风浪数值模型—SWAN模型应用于模拟内陆湖泊风浪生成和传播变形时的特点。该模型存在不能有效地模拟近边界处风浪场的缺点，因此在模拟内陆湖泊的风浪场时，应首先适当地扩大计算范围。在确定计算范围时，应以能正确地模拟风浪场和节约计算时间为原则。

2)在对观测的风场和风浪场进行统计时，剔除了不合理的观测数据。在统计的有效时刻内，靠近岸边的2号观测站的风速比水域开阔处的1号站和3号站的风速分别小1.76 m/s和2.08 m/s，有效波高分别比1号站和3号站的有效波高小0.19 m和0.22 m。

3)计算并统计了利用不同方法所得有效波高的绝对误差、分散系数、计算结果和观测结果的一致程度。在根据观测的风场计算1号站和3号站的有效波高时，经验公式的计算结果和以这两个站的风场平均值作为输入、利用SWAN模型进行计算所得结果的精度相当，而以三个站的风场平均值作为输入、利用SWAN模型进行计算的结果的精度较低，其原因是距离岸边较近的2号站的风速明显小于这两个站的风速。在利用SWAN模型计算2号站的风浪时，应以该站的风场作为输入，而不能够以三个站的平均风场作为输入，其原因仍然是该站的风场明显不同于水域开阔处的风场。因此，在利用SWAN模型、根据实测的风场计算水域面积较大的内陆湖泊的风浪场时，不能盲目地以各观测站点风场的平均值作为输入，而应当谨慎地布置观测站点，并小心地选择所输入的风场。为了能够预报风浪场，需使用气象预报部门所提供的数值预报风场。气象部门所提供的风场与实测值相比，存在一定的误差，误差产生的主要根源是气象预报模式本身的问题。在根据预报的风场计算风浪场时，计算结果的误差部分是由风浪场的计算方法引起的，部分是由所采用的风场的误差引起的。如果要根据预报风场实时预报风浪场，那么就应当采用SWAN模型进行计算。这是因为该模型是进行全区域联立求解，能够平滑由于部分位置的较大的风场误差所引起的风浪场的误差。而利用经验公式计算风浪场，则是仅仅依赖所计算位置的风场，如果该位置的风场具有较大误差，那么计算的风浪场肯定也会产生较大的误差。虽然根据预报的风场所计算的内陆湖泊风浪场的误差比根据实测风场所得计算结果的误差大，但仍然小于他人根据实测的风场所计算的风浪场的误差。因此，无论是根据实测的风场还是根据预报的风场，利用SWAN模型都较好地模拟了太湖的风浪场。

［1］中国科学院南京地理与湖泊研究所.太湖［M］.北京:海洋出版社，1993:1-14.

［2］中华人民共和国水利部.堤防工程设计规范［S］.北京:中国水利水电出版社，1999:55-56.

［3］The SWAN team.SWAN Technical Documentation［R］.The Netherlands:Delft University of Technology，2010.

［4］Booij N，Ris R C，Holthuijsen L H.A third-generation wave model for coastal regions 1:model description and validation［J］.Journal of Geophysical Research，1999，104(C4):7649-7666.

［5］Ris R C，Holthuijsen L H，Booij N.A third-generation wave model for coastal regions 2:verification［J］.Journal of Geophysical Research，1999，104(C4):7667-7681.

［6］Lin W Q，Sanford L P，Suttles S E.Wave measurement and modeling in Chesapeake Bay［J］.Continental Shelf Research，2002，22:2673-2686.

［7］Ou S H，Liau J M，Hsu T W，et al.Simulating typhoon waves by SWAN wave model in coastal waters of Taiwan［J］.Ocean Engineering，2002，29:947-971.

［8］Holthuijsen L H，Herman A，Booij N.Phase-decoupled refraction-diffraction for spectral wave models［J］.Coastal Engineering，2003，49:291-305

［9］贾 晓，潘军宁，Niclasen B.SWAN模型风能输入项的改进与验证［J］.河海大学学报:自然科学版，2010，38(5):585-591.

［10］李一平，逢 勇，刘兴平，等.太湖波浪数值模拟［J］.湖泊科学，2008，20(1):117-122.

［11］Bottema M，Vledder G.A ten-year data set for fetch-and depth-limited wave growth［J］.Coastal Engineering，2009，56(6):703-725.

［12］张洪生，文武键，辜俊波.用两种不同方法计算淀山湖风浪［J］.海洋工程，2011，29(1):122-129.

［13］张洪生，辜俊波，文武键.淀山湖风浪场的数值模拟［J］.湖泊科学，2011，23(5):783-788.

［14］张洪生，周华伟，于小伟，等.太湖风浪预测系统应急完善技术报告［R］.上海交通大学船舶海洋与建筑工程学院，2009.

［15］文圣常，余宙文.海浪理论与计算原理［M］.北京:科学出版社，1984:309.

［16］Moeini M H，Etemad-Shagidi A.Wave parameter hindcasting in a lake using the SWAN model［J］.Scientia Iranica，Rransaction A:Civil Engineering，2009，16(2):156-164.

［17］ZHANG Hong-sheng，ZHU Liang-sheng，YOU Yun-xiang.A numerical model for wave propagation in curvilinear coordinate［J］.Coastal Engineering，2005，52:513-533.

［18］Skamarock W C，Klemp J B，Dudhia J，et al.A description of the advanced research WRF version 3［M］.NCAR/TN-475+STR，Boulder.Colorado，USA，2008.

Comparisons of calculated wave heights in Taihu Lake

ZHANG Hong-sheng1，DAI Su2，ZHANG Yi2
(1.Ocean Environmental and Engineering College，Shanghai Maritime University，Shanghai 201306，China;2.Taihu Basin Authority，Shanghai 200434，China)

The characteristics of the wave model Simulating Waves Nearshore(SWAN)are found when the model is applied to simulate the wind wave generation and propagation in the inland lakes.In view of the drawback of the SWAN model that it can not effectively simulate the wave field near the solid boundaries，the calculation domain of Taihu Lake is determined after modeling test.When the calculation domain is determined，the principles should be obeyed that the wind waves in the lake district can be simulated properly and that the computing time is not wasted.The wind field and wind wave field are measured.The significant wave heights are calculated by use of normal formula and the SWAN model，with the measured and predicted wind field input，respectively，and the calculated results are compared to the measured data in detail.It is indicated that the precisions of the calculated results according to the normal formula are similar with those of SWAN model if the measured wind field is input.When the wave field is simulated by use of SWAN model according to the measured wind field，the measuring locations should be arranged carefully and the wind field should be selected properly.The precisions of the calculated results according to the SWAN model are greater than those of the normal formula if the predicted wind field is input.

wind wave field;wind field;SWAN model;normal formula;Taihu Lake

TV148

A

1005-9865(2012)04-0068-14

2011-09-30

国家自然科学基金资助项目(51079082，40676053);上海交通大学海洋工程国家重点实验室资助项目(GKZD010012，GK2D010024);华东师范大学河口海岸学国家重点实验室开放基金资助项目(200907)

张洪生(1967－)，男，山东高唐人，教授，从事水波动力学的理论及其应用研究。E-mail:hszhang@shmtu.edu.cn