基于年龄移算法的人口预测

蒋远营

（桂林理工大学理学院统计学教研室，广西 桂林 541004）

1 人口预测模型的建立与求解

中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。根据已有数据，运用数学建模的方法，对中国人口做出分析和预测是一个重要问题。人口预测是通过采集基础资料、建立预测模型和确定预测参数等基本环节来完成。人口预测的基本方法和模型较多，一般较为流行和实用的有年龄移算法、矩阵方程、人口发展方程和指数方程等几类。我们基于《中国人口和就业统计年鉴2010》中的部分数据利用年龄移算法模型对我国人口情况进行预测。本文将从中国的实际情况出发，参考相关数据，建立中国人口增长的数学模型并利用求得的增长模型对中国人口增长的中短期和长期趋势做出预测。

1.1 年龄移算法的基本原理

年龄移算法，是指以各个年龄组的实际人口数为基数，按照一定的存活率进行逐年递推来预测人口的方法。该算法能够准确地对未来人口作出预测，主要基于人口是时间的函数原理。即人口的年龄是用时间来表示的，一年即为一岁，时间过一年，人的年龄也就增长了一岁。因此，随着时间的推移，人口的年龄也在不断地发生着转移。当在一定死亡率水平条件下，人口的年龄在其不断地转移过程中，人口数也就相应而随之发生着变化。由此原理，即可把由某一年度、某一年龄组的人口数，在相应年龄组的死亡率水平条件下，通过转移到下一个年度、下一个年龄组的人口数测算出来。故将此一预测人口的方法，谓之年龄移算法。

1.2 年龄移算法模型的基本描述

年龄移算法模型的基本表达式为：Px+1(t+1)=Px(t)·Sx，当x=0,1,2,...,ω-1时，上面模型可具体描述为：

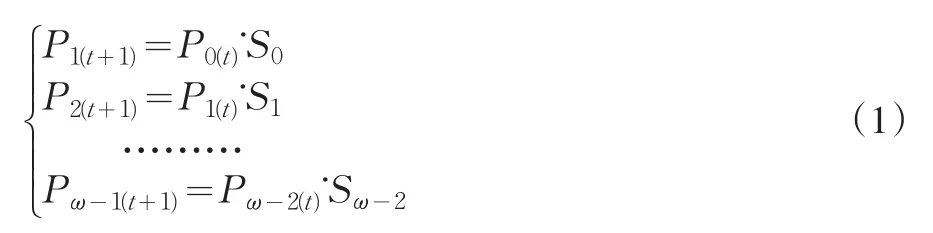
式中：Px+1(t+1)为预测年度x+1岁的人口数；Px(t)为预测基年x岁的实际人口数；Pω-1(t+1)为预测年度最高年龄组之预测人口数；Sx为x岁的存活率,Sx=1-mx.(1)式所描述的年龄移算法模型。模型中每一行的预测关系式很明确，即：预测年度1岁组人数，系由预测基年的0岁组人口数乘上0岁组人口存活率而来；预测年度2岁组人口系由预测基年的1岁组人口数乘上1岁组人口存活率而来；其余类推。这样，就可以把预测年度的人口数，从最低年龄到最高年龄组逐一推算出来。

（1）出生人数预测

(2)死亡人数预测基本模型

人口死亡现象会直接引起人口总体的数量发生变动。而人口总体又是由按年龄、分性别构成的一个复杂整体，即如，按年龄分布由0,1,2,...,ω-1的结构，而其中又有男女不同性别的区分。因此，由人口死亡现象所引起的人口数量变动在各个不同年龄间和性别间也就有着差异。然而，由于死亡因素而使各个年龄组人口数变动的特征却又是一致的。即当在封岁组外，闭人口条件下，也就是在不存在或不考虑迁移因素条件下，除0岁组外每一个年龄组的人口数的变动，只有绝对减少的变动。因此，根据各个年龄组人口数量变动的这一特点，对于同一年龄组的人口数，在不同的时间条件下，如今年x岁年龄组的人口数，到下一年度进入x+1岁年龄组的时间条件下所引起的人口数的变动之差，即可由此得到相应的死亡人数的预测与计量。于是，这就得到下面一个重要结论：x岁年龄组的死亡人数等于这个年龄组同其相邻的x+1岁年龄组的人口数之差。这就是死亡人数预测的基本理论依据。

根据上述死亡人数预测的基本理论结论，即预测年度某年龄组的死亡人数，可以通过同一年龄组的生存人口数与大一岁的相邻年龄组的生存人口数的相减来求得，也就是把死亡人数预测变成为通过由对存活人口数的技术处理来获得。于是，即可得到关于死亡人数预测模型的如下描述：

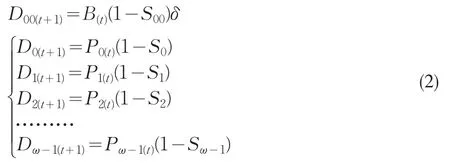
式中：D00为出生当年过程中的死亡人数；Dx为预测年度x岁的死亡人数；B(t)为预测年度之出生人数（由出生人数预测取得）；S00为出生当年存活率，Sx为x岁人口之存活率，Px(t)为t年x岁的人口数.这里的Px(t)人口数,在预测的第一年时，其为预测基年的实际人口数,在此以后的预测年份时，即为预测年度的预测人数。

(3)总人口数预测：采用按年龄人口预测求和法

总人口预测可以由分年龄、分性别的人口数预测结果直接取和而得。并且，由于分年龄、分性别人口数预测所使用的预测模型一般数理含量较高，预测变量定义严格，技术处理规范，预测结果的精度较高。所以，由按龄人口数预测结果进行求和，由此得到的总人口数预测，其预测精度可以得到充分保证。

1.3 短期（近6年）的预测结果：

表1 2010～2015年人口预测值 （单位：人）

我们在具体预测时，把城市、乡镇、农村分别看作各自封闭的群体分别计算，然后加总，表1即为近6年的预测值：

1.4 中长期预测

在第3节短期预测中，人口迁移可以忽略，把城市、乡镇、农村分别看作封闭的群体分别计算，然后加总，但是在中长期的预测过程中由于城镇化等原因不能再把城市、乡镇、农村分别看作封闭的群体，为了简化起见，先将分市镇村的死亡生育男女比例等按加权平均的思想重新得到一个全国的死亡生育男女比例表格，再进行计算，预测值如表2。

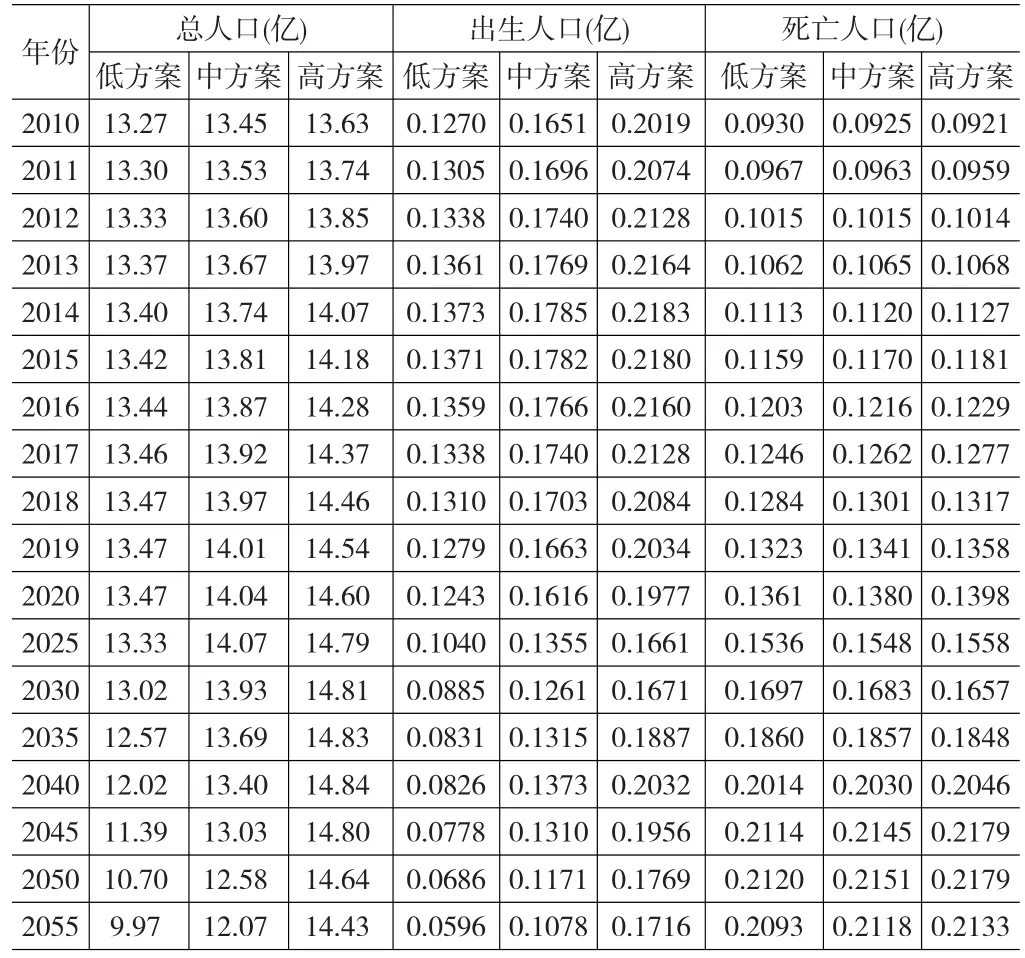
表2 2010～2055年相关人口预测值 （单位：亿人）

低方案：TFR=1.386(2009年水平)中方案：TFR=1.8高方案：TFR=2.2

修正生育率法，是指依据人口控制目标要求而对实际生育率水平加以修正来进行预测的方法。修正的前提，是在当前生育率水平不能适应未来社会经济发展水平要求而提出的，如国在解放初的总和生育率将近4.5的生育水平，这与我国当前的国情来讲，是为我国未来时期的社会经济发展的客观实践所不能接受的。所以，这就要求必须根据人口控制目标的不同方案，对实际生育率加以修正与调整，然后纳入预测模型进行测算。

2 动态修正生育率下的中长期人口预测算法

我们可以看到在中长期预测中我们使用的修正总和生育率TFR取值有3个水平，TFR=1.386为低水平，表示为低低生育模式，也就是现行的计划生育政策环境；TFR=2.2为高水平，为人类为保持人口数量平稳的更替繁衍时的生育水平；而TFR=1.8为介于两者之中的一种模式，也就是半计划生育模式环境，或者是差别计划生育模式环境。

事实上考虑到计划生育政策的连贯性、渐进性、科学性，我们可以设计一个比上述高中低模式更为科学和实用的调整方法：在2009～2015年期间考虑到目前计划生育政策的连续性和长期性，我们设定为目前的修正生育率水平TFR=1.386，在2016～2020年期间TFR=1.52，在2021～2025年期间TFR=1.60，在2026～2030年期间TFR=1.66，在2031～2035年期间TFR=1.73，在2036～2040年期间TFR=1.80，在2041～2045年期间TFR=1.88，在2046～2050年期间TFR=1.94，在2051～2055年期间TFR=2.00，详情见表3。

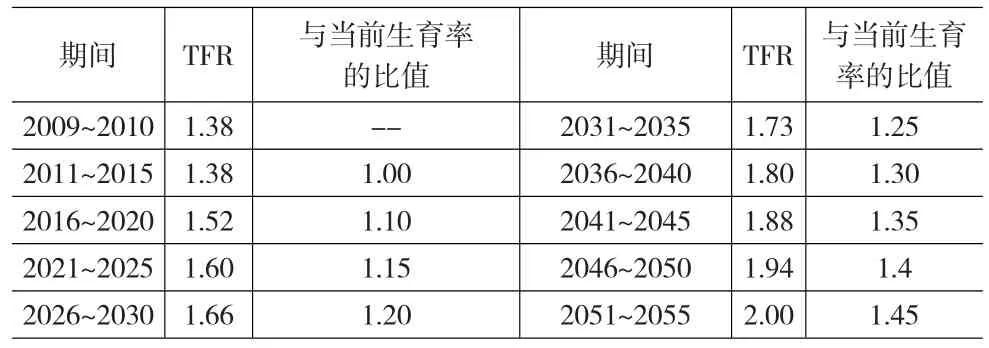
表3 2010～2055年各阶段 TFR值及环比值

3 结论

（1）方法直观简单易于实现，易于编程。优于一些数学预测（曲线预测，如指数曲线、灰度模型GM(1,1)），主要是这些方法只能对人口总数做预测，而不能像本方法给出详尽的人口的各个年龄段的数量分布情况。

（2）由于短期内人口的出生率、死亡率可以近似看作恒定的，人口的迁移也可以不考虑，或者人口迁移的影响很小，所以基于2009年城市、乡镇、农村人口统计数据，用年龄移算法模型预测的人口增长结果还是相当精确可靠的，但是缺点是非常依赖基年统计数据的精度。

（3）这种城市、乡镇、农村分开单独计算长期来说是不可取的，因为没考虑到人口迁移（城镇化）问题，为了避免这个问题我们在对人口做中长期预测时，我们根据3个类别的人数比例、出生率、死亡率、性别比例计算出一个全国的2009年0～90岁人口的一个综合生命表，这样再利用年龄移算法计算出2009～2050年人口增长状况，根据最后递推结果可以算出中长期的人口增长问题、老龄化问题、男女比例问题、育龄妇女比例数据。缺点是依然十分依靠2009年的统计数据的精度，还有长期预测时，随着误差的叠加，预测的精度可能难以控制，但是能够大致了解稳定的社会环境下的人口增长趋势，为我国人口政策具有指导意义以及提供可靠的理论依据。

[1]李永胜.人口统计学[M].成都：西南财经大学出版社，2002.

[2]黄荣清等.人口分析技术[M].北京：中国统计出版社，1989.

[3]宋健.人口预测和人口控制[M].北京：科学出版社，1982.

[4]田雪原.中国人口控制和发展趋势研究[M].北京：经济科学出版，1985.

[5]姜启源.数学模型[M].北京:高等教育出版社，1993.

[6]国务院人口普查办公室.第五次全国人口普查国家级课题论文集[M].北京:中国统计出版社，2003.

[7]方建卫.基于最小二乘法GM(1,1)模型在人口预测中的应用[J].贵州大学学报，2007(4).

[8]国家统计局.中国人口和就业统计年鉴2010[M].北京:中国统计出版社,2011.

[9]蒋远营,王想.人口发展方程模型在我国人口预测中的应用与研究[J].统计与决策,2011,(15).