基于收益管理的信用信息商品动态定价方法
2012-01-07付尔泰龙海明
付尔泰,龙海明
(湖南大学金融与统计学院,长沙 410079)
0 引言
市场经济是信用经济。如今,无论是企业生产过程还是个人消费过程,难免会产生信贷需求,由此促使人们对信用重要性的认知越来越高,并进而促进人们对信用信息商品化的认同感不断增强,对信用信息商品的需求也逐步增大。信用信息商品又称“信用商品”或“征信产品”,是指以信用信息为原材料进一步进行加工增值、能够真实全面反映信用主体信用状况的商品,比如个人的信用评分报告、企业的信用评级报告等[1]。狭义的信用信息商品的内容仅局限于金融交易活动,更广义的信用信息商品内容还可以包括个人的道德状况、守法状况等内容。本文将主要讨论狭义的信用信息商品定价问题。
1 特征分析:信用信息商品定价的现实基础
商品定价方法的选择涉及商品的特性把握,因此分析信用信息商品的特性是选择定价方法的基础。
1.1 信用信息商品的成本特性
信用信息商品属于一种特殊的信息商品,它的成本构成具有特殊性[2]。信用信息商品的生产具有高固定成本、低变动成本和接近于零的边际成本。但征信机构的固定成本投入并不是产品销售量的函数,更重要的是总变动成本也不是产品销售量的函数,或者只有微弱的函数关系,即:

从(1)式不难理解,一家征信机构一天收到上万次的信用报告查询和未卖出一份信用报告所耗费的变动成本应该是差不多的。如果运用现代西方经济学的边际成本定价方法会发生如下情况:
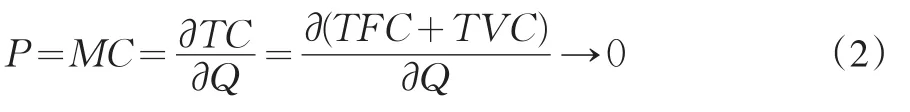
即无论何种规格与质量的信用信息商品的定价都趋近于零,显然这样的定价无法让征信机构生存下去。
1.2 信用信息商品的价值易逝性
信用信息具有非常大的时效性特点,或者说其商品价值具有易逝性特点。基于此特点,信用信息商品的内容需要不断被更新以维持其价值,内容越陈旧的信用信息商品价值越低。所以,在信息更新之前没有将信用信息商品销售出去即意味着价值的损失,征信机构应该随时尽可能多地增加产品销售量,否则随时都面对着产品价值的消逝。
1.3 信用信息商品容易实现差别化生产
信用信息商品的生产原料来自原始信用信息数据库,征信机构一旦建成较完整的原始信用信息数据库就可以设计各种产品模型并生产多种满足不同需求的信用信息商品,甚至同一购买者可以分条选择信息以生成所需的信用报告。这样看来,信用信息商品具有很强的差别化特征,理论上征信机构可以提供无限种类的信用信息商品。综上,信用信息商品属于具有无限供给能力的差别化易逝性信息商品。
2 收益管理:信用信息商品定价的动态原理
收益管理(Revenue Management)是指企业对市场进行细分,对各个子市场的需求特征做出分析和预测,生产差别化的商品并确定适当的商品价格实现收益最大化[4]。收益管理应用的产品对象主要是有易逝特点的商品,另外分为不可补货和可补货两类商品,本文依据信用信息商品的产品特性将其视为无限补货的易逝品,并将收益管理思想应用于其定价全过程。收益管理的基本价格策略是差别定价,且动态定价是其中的一个重要分支。动态定价方法(Dynamic Pricing)最早由Kincaid和Darling[5](1963)开始研究并应用于解决易逝品定价问题,随着市场中商品的极大丰富、商品内容日益多样化,产品生命周期越来越短,消费者的个性化需求越来越受到重视,动态定价开始应用于更多的产品种类[6]。动态定价的基本原理是厂商面对不同消费者以及在不同时间下的不同需求偏好,对商品实施变化定价以达到收益最大化的目的,与收益管理思想具有一致性,是解决收益管理问题的重要手段之一。
随着信用信息商品种类的丰富和多样化,同时消费者的需求偏好对商品属性更加敏感并且会随时间变化而变化,征信机构面临的市场需求更加多变和不可预测,在这种情况下基于收益管理的动态定价方法是一个合理的选择。
3 模型构建:信用信息商品定价的核心内容
3.1 模型构建思路
本文信用信息商品的定价主要分为三个步骤:第一步,建立某征信机构差异化的产品集,该产品集是其向市场供应的全部产品种类,产品差异来自于信用信息商品的信息元数量和质量两个属性;第二步,建立消费者效用函数和基于效用函数的产品选择概率函数,用以描述消费者对不同产品的偏好和选择行为;第三步,建立收益最大化的动态定价模型,通过模型得到整个市场最优定价的分布,并整理得到最终定价。
3.2 产品集设计
假设信用信息商品主要有两个属性,一是其信息元数量级别,即所包含的信息容量大小,二是信用信息商品的质量。在这里,一般化的信用信息商品集合设计如表1所示。

表1 某征信机构的信用信息商品集
q1,q2,…qn为信用信息商品的质量级别,共n个质量级别并且q1< q2<…< qn;Q1,Q2,…Qm为信用信息商品包含的信息元数量级别,共有m个信息元数量级别,并且Q1<Q2<…<Qm;Nij表示信息元数量级别为Qi、质量为qj的信用信息商品。某信用信息商品可以用如下方法表示:

在(3)式中,Rij为某信用信息商品的物元化表示,ci为信息元的属性,vi为对应属性的量值,(ci,vi)称为信息元,是信用信息商品中独立的最小的信息单位,(3)式所表示的信用信息商品Nij包含s个信息元。
关于信用信息商品的质量级别,主要包括信用信息商品的时效性、准确性、技术含量、分析深度、包含的时间跨度、实用性等内容,据此来区分不同商品的质量级别。
3.3 购买者选择行为及其效用函数参数市场分布假设
目前消费者面对的商品可选方案集合为N,包含k个不同的可选方案,其中方案j对于该消费者的效用为Uj,根据效用最大化的原则,消费者选择方案j的条件为:

j方案的效用Uj可以分解为两部分:

其中Vj是效用的可观测部分或确定性部分,εj是效用的不可观测部分或随机部分,并且服从独立极值同分布(Gumbel分布),利用多项Logit(MNL)概率选择模型[6]的到的信用信息商品选择概率函数为:
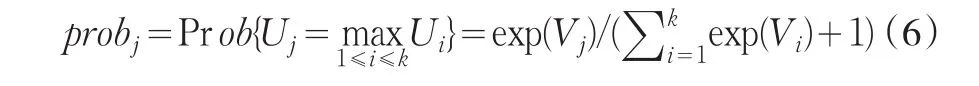
其中,probj为消费者选择方案j的概率。
MNL选择模型效用函数的确定也是一个难点,多设定为参数的线性函数,函数的形式需要在多次的模拟试错过程中获得。Mahajan和Van Ryzin(1999)的研究假设产品i的对于消费者的效用为产品价格p的线性函数[7]:

其中参数α表示产品的质量、品牌形象和市场流行度,β表示价格敏感系数,Z表示随机变量,与εj同分布。
本文假定信用信息商品的效用依赖商品的信息元数量、质量和价格,因此消费者的效用偏好也由这三个属性来解释。依据偏好的不同,信用信息商品的购买者有信息元数量敏感型、质量敏感型、价格敏感型和中度敏感型等。消费者的效用函数是由三个参数表示的非线性函数,函数设计如下:

式(8)中Uij为某征信机构信用信息商品集合中商品Nij的效用,α为尺度参数,即效用大小的度量由α来定调,b表示信息元数量敏感参数,d表示质量敏感参数,β表示价格敏感参数,Z为随机项。不同消费者的b、d、β参数都各不相同,并且三个参数都服从独立正态分布,描述了消费者群体的偏好类型也服从一个正态分布,也就是大多数消费者都属于中度敏感型。
该效用函数有如下性质:

(9)式表明:①在三项参数相同的条件下,信用信息商品的信息元数量级别越高效用越高,质量级别越高效用越高,价格越高效用越低。②在同一信用信息商品条件下,消费者的信息元数量敏感参数越大,随着信用信息商品信息元数量级别越高效用增长越快;消费者质量敏感参数越大,随着信用信息商品的质量级别越高效用增长越快;消费者价格敏感参数越大,效用越低。
3.4 收益最大化动态定价模型
针对表1所示的信用信息商品集合,矩阵P为对应商品集的价格矩阵:

其中,Pij为信用信息商品Nij对应的出售价格,动态定价模型的目标就是确定最终合适的价格矩阵P。征信机构面对的单个消费者或者具有相同效用函数的消费群体的期望收益函数为:

征信机构收益最大化的条件为:

征信机构在时期[Ti,Ti+1]最大期望收益为π(P*),消费者对每一种信用信息商品的选择首先要根据自身的金融交易需要来确定,其次依据自身的效用函数来确定自己的购买意愿。在确定最终价格之前,征信机构可以利用已有信息估计消费者选择函数的参数并用以试探市场能获得最大收益的价格。以产品N11为例,征信机构以价格将产品N11分别投向市场,通过MNL选择函数可以确定对产品N11有需求的市场群体在各个价格下的选择概率,即为,则产品N11的最优定价为:
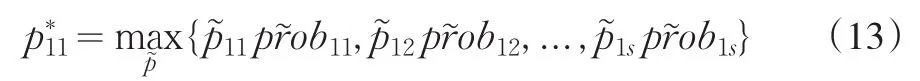
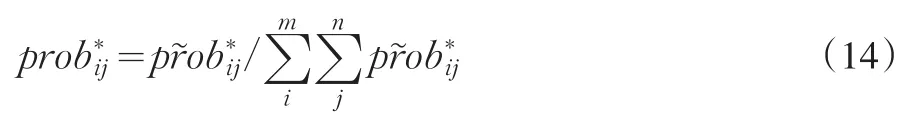
在单个消费者或者具有相同效用函数的消费群体条件下的最大期望收益为:

但是征信机构面对的整个市场存在具有各种不同偏好的消费者,因而对应的最优价格解也不同。在整个市场条件下,征信机构在[Ti,Ti+1]时段内的需求密度为λ,它将面对λ个最优价格解P*。以产品N11的价格为例,其在针对λ个消费者最优定价条件下的价格向量为:,通过加权平均值的方法对这些离散的最优价格进行整来确定商品N11最终的单一价格,同理,可求出时段[Ti,Ti+1]内商品集对应的收益最大化的最优价格解:

4 算例分析
4.1 算例参数假设
假设该案例中征信机构的产品集由5个信息元数量级别和6个质量级别组合而成,共30个单一产品,具体产品如表2所示。
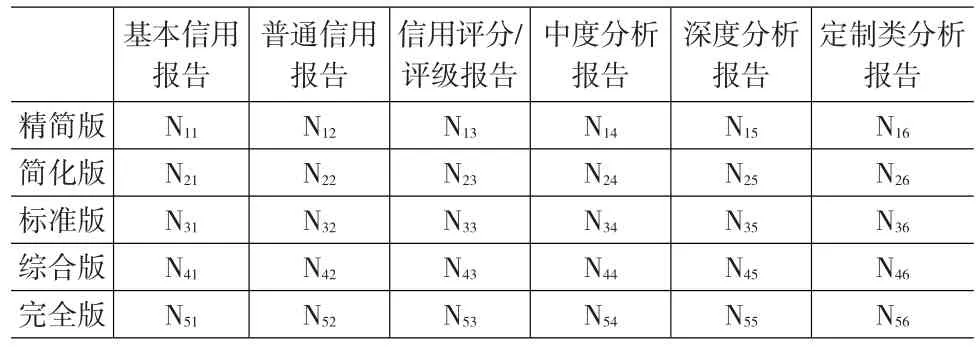
表2 某征信机构信用信息商品集合
具体的产品名称这里用Nij代表,如N22表示简化版的普通信用报告,信息元数量级别和质量级别解释如表3所示。
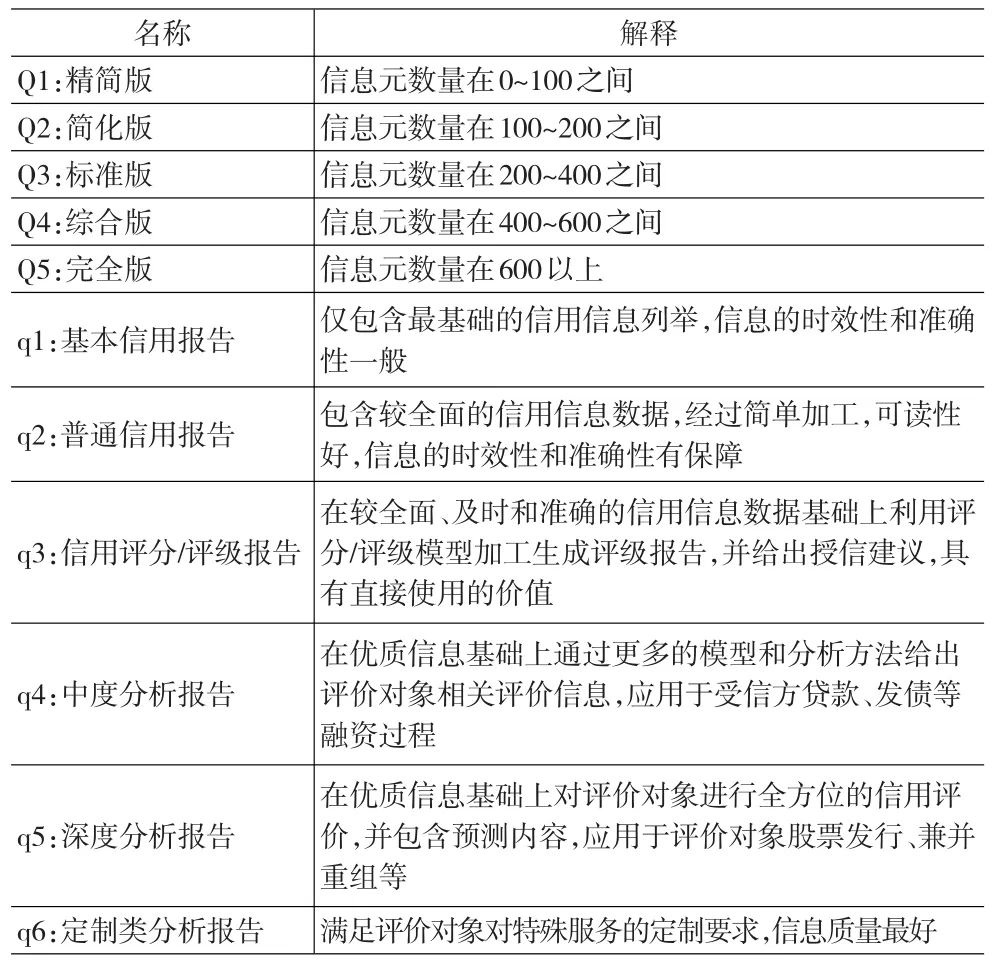
表3 信息元数量级别和质量级别的解释
其他参数设定如表4所示。

表4 参数数值的设定
4.2 单一客户最优定价算例分析
为了说明对单一消费者的最优定价,本文以信息元数量敏感型和质量敏感型两个具有明显偏好的消费者为例做数值分析,两个消费者的参数如下:

C1:信息元数量敏感型消费者C2:质量敏感型消费者b=0.8,d=0.2,β=1.018 B=0.2,d=0.8,β=1.018
将参数带入模型程序得到消费者C1和C2的最大期望收益图,如图1、图2所示。

图1 消费者C1的期望收益平面
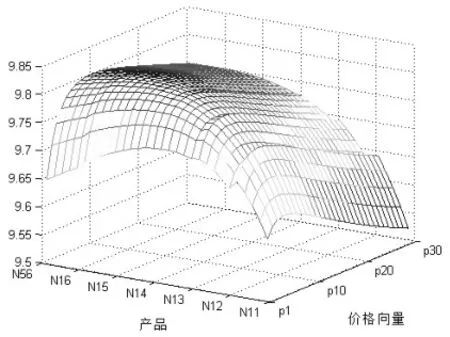
图2 消费者C2的期望收益平面
由图中各产品对应的最高收益点得到对C1、C2的最优定价矩阵,分别为:

4.3 市场最优定价算例分析
下面对整个市场进行模拟。时期为[0,T1],市场总需求为λ=1000个随机消费者。本文将得到1000组最优价格解。以产品N11为例,1000个最优价格出现情况如图3所示。
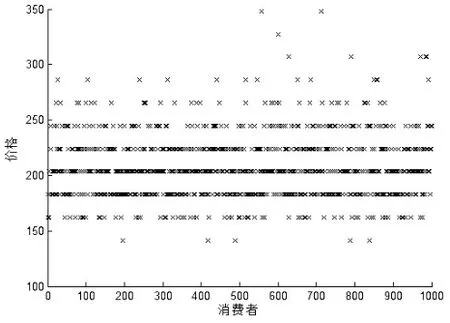
图3 产品N11的最优定价市场分布
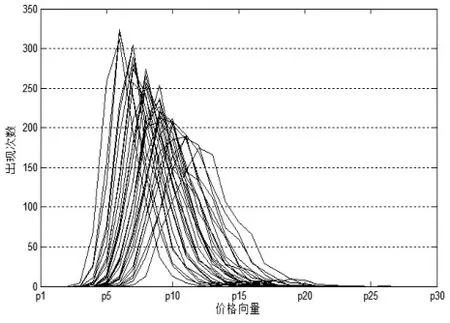
图4 产品集的最优定价分布
全部30个产品的最优价格分布如图4所示,各个产品的价格都表现出正态分布的特征,图中横轴为价格向量,纵轴为在各价格点出现最优定价的次数。
到目前为止,本文得到了各产品的最优离散价格,但是这一离散价格还不能付诸使用,因为征信机构不能同时对一个产品进行多个定价,否则定价是无意义的,消费者永远会选择最低价进行购买。所以本文选用加权平均法对离散价格进行加权平均整理,权数为价格出现次数的比重,因而出现次数越多的价格对最终定价影响越大。经过整理在时间段[0,T1]期内的最终定价如表5所示。

表5 某征信机构[0,T1]期内的信用信息商品集合定价
随着征信机构掌握了新的市场信息,并对市场效用函数参数分布预测发生变动,在[T1,T2]的最定价会与[0,T1]期的定价有所不同,在此不再重复计算。
5 结束语
本文的信用信息商品定价模型是基于市场效用函数建立起来的,定价的准确性依赖于具体效用函数形式的优良性和参数估计的准确性。由于我国相关市场数据的贫乏,本文建立的效用函数及其参数的假设都具有一定的主观性,但本文的目的并不是模拟现实的市场,而是给出信用信息商品定价的一个思路。模型没有将征信机构的成本考虑进来,是由于定价对象的特殊性造成的成本定价理论不适用于信用信息商品的定价。因此,总的来说该定价模型的理论基础和定价方法具有一定的可行性。定价模型的进一步研究可以考虑完善模型结构和相关函数和参数,并逐渐和真实市场相结合。由于该领域的研究处于空白,在定价的方法上还可以尝试将神经网络模型、最优规划模型等引入定价模型中。
[1]人民银行征信中心.征信前沿问题研究[M].北京:中国经济出版社,2010.
[2]解梅娟.数字产品定价问题初探[J].生产力研究,2011,(4).
[3]罗利,萧柏春.收入管理理论的研究现状及发展前景[J].管理科学学报,2004,(5).
[4]Kincaid,W.M.,D.A.Darling.An Inventory Pricing Problem[J].Jour⁃nal of Mathematical Analysis and Application,1963,(7).
[5]李根道,熊中楷,李薇.基于收益管理的动态定价研究综述[J].管理评论,2010,22(4).
[6]聂冲,贾生华.离散选择模型的基本原理及其发展演进评介[J].数量经济技术经济研究,2005,(11).
[7]官振中,史本山.基于顾客选择模型易逝性产品收益管理订购和定价策略[J].系统工程理论与实践,2007,(9).
