庞西垌地区地球化学异常圈定方法讨论

王 琨，周永章，高 乐

(1.中山大学地球科学系，广东 广州 510275;2.广东省地质过程与矿产资源探查重点实验室，广东 广州 510275;3.中山大学地球环境与地球资源研究中心，广东 广州 510275)

庞西垌地区地球化学异常圈定方法讨论

王 琨1，2，3，周永章1，2，3，高 乐1，2，3

(1.中山大学地球科学系，广东 广州 510275;2.广东省地质过程与矿产资源探查重点实验室，广东 广州 510275;3.中山大学地球环境与地球资源研究中心，广东 广州 510275)

庞西垌地区位于钦杭成矿带南段，是主要的贵金属、有色金属成矿区。区内构造复杂，岩浆活动频繁。基于庞西垌地区水系沉积物测量数据，以Au、Ag元素含量为例，分别利用传统统计学方法、趋势面法和分形方法计算其异常下限值，并圈定地球化学异常。通过对3种方法计算过程及应用效果的对比，分析了3种方法应用于本研究区的效果，进而揭示了复杂地质背景下，最适用于圈定地球化学异常的方法。

地球化学异常;分形;迭代法;趋势面法;庞西垌地区;粤桂

0 引言

计算地球化学异常下限进而圈定地球化学异常在矿产勘查和预测中占有十分重要的地位。实际工作中，依据统计学方法确定异常下限的方法是建立在概率分布基础上的，常用的有拐点法、移动平均法、趋势面法、克里格法、迭代剔除法和衬度系数法等(Mieschat，1981;Govtt et al，1975;纪宏金等，2001;谢学锦，2002;赵鹏大，2004)。由于传统计算方法只考虑地球化学数据的统计学规律，忽视了其空间分布规律，所以异常下限计算方法显得过于机械化。随着分形理论(Qiuming等，1996;陈志军，2007;韩东昱等，2004;李宗敏等，2008)、小波分析(陈建国等，1999;雷丽等，2000)方法的融入，更多的学者考虑到元素在地壳中的区域性或趋势性的变化。国内外研究表明，区域地球化学场并非处处可微，数据服从分形分布(Qiuming等，1994;李长江等，1999;申维，1999;於崇文，1999)。利用分形方法研究区域地球化学场异常下限已经成为一种发展趋势(孙忠军，2007)。在此基础上，笔者以传统统计学方法、趋势面法、分形方法为例，通过对庞西垌地区Au、Ag元素的异常下限进行计算，进而圈定异常，来揭示3种方法的优缺点及适用范围。

1 区域地质特征

庞西垌地区位于钦杭成矿带南段，具体位于粤西云开隆起区的南缘，北东向信宜—廉江断褶带南段，为晚古生代以来的长期隆起区。区内地层出露相对齐全，构造复杂，岩浆活动频繁，是贵金属、有色金属的主要成矿区，有多处大中型矿床，如廉江西部金山金矿床，庞西垌金银矿床。受控北东向廉江—信宜断裂构造带与东西向廉江—茂名断裂构造带交汇地段，形成了廉江铁、铅、锌、硫成矿区。此外，廉江塘蓬岩体内及其周边矿床(点)星罗棋布，以金、银贵金属为主，形成金、银、钨、钼、铅锌多金属矿区。

以钦杭结合带南段庞西垌地区1∶5万水系沉积物测量数据为例，分别对7 234个Au、Ag地球化学数据按3种方法进行处理分析，进而对比各种方法的实际效果。

2 传统统计学方法圈定地球化学异常

圈定地球化学异常的传统方法(迭代剔除法)基于元素含量在所研究范围内呈正态或对数正态分布，通常认为常量元素服从正态分布、微量元素服从对数正态分布。在计算过程中，首先检验各个元素含量的概率分布是不是服从正态或对数正态分布，对于服从的元素可直接计算其异常下限与背景值;对于不服从的元素需逐步剔除特高值，再进行统计计算，如此迭代下去，直到其服从正态或对数正态分布。异常下限一般取平均值与1.5～3.0倍的标准离差之和。

地球化学数据的分布形式检验常用的方法有偏度、峰度检验法和概率格纸检验法(王崇云，1987)。笔者采用Q-Q概率图对元素含量进行分布检验，由于所研究元素均为微量元素，故只检验各元素的对数正态Q-Q图。当符合对数正态分布时，图中各点近似成一条直线(苏金明，2004)。研究区Au、Ag元素的Q-Q图(图1)显示，Au、Ag元素的地球化学数据分布均不服从对数正态分布，需要进行迭代剔除。

图1 庞西垌地区Au、Ag元素原始数据对数正态Q-Q图

用传统统计学方法剔除一些数据后，计算出研究区Au、Ag元素的异常下限见表1。

表1 庞西垌地区Au、Ag元素传统统计学方法计算结果

通过多次迭代，剩余的元素含量值均在平均值加3倍标准离差之内，再次统计对数正态Q-Q图可知：Au、Ag元素数据经迭代剔除处理后，近似服从正态分布，但部分数据分布的分位数与对数正态分布的分位数之间的关系还是有一定程度的偏离直线(图2)。

根据传统方法求出的异常下限，并取计算出的下限及其2倍、4倍为下限，在MapGIS平台下圈定庞西垌地区Au、Ag元素的地球化学异常(图3)，利用GIS平台可灵活管理各图层，轻松叠加矿点进行分析。其中五角星图案表示金矿点，三角图案表示银矿点，其中包含金银矿点。

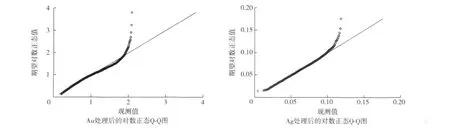
图2 庞西垌地区Au、Ag元素传统方法处理后对数正态Q-Q图

分析庞西垌地区Au、Ag元素的地球化学异常图可以看出，传统方法的下限计算过程较为机械，完全通过统计量得出，没有考虑元素含量的内部富集规律和空间变化规律，有一定的局限性。如图3所示，Au元素的异常下限分级较为符合研究区的元素含量变化特征，所以与矿点吻合度较高;Ag元素的异常下限过高，显然忽视了较多弱异常。

图3 传统方法圈定庞西垌地区Au、Ag元素异常示意图

3 趋势面法圈定地球化学异常

趋势面法将化探数据包含的信息分为3个部分，分别为反映区域性变化的、反映局部性变化的、反映随机性变化的，即Zi=Ti+Ni+ei。其中，Zi为观测值;Ti反映总体变化规律，即区域性变化;Ni反映局部性变化;ei为随机因素控制的变化。在实际应用中，首先将观测值(元素含量)分解为两部分：区域分量Ti和剩余分量，其中剩余分量包括Ni和ei两部分，而需要的就是具有地质意义的Ni。利用Surfer软件拟合多元回归曲线(任印国等，2006)，并通过残差计算来进行趋势面法圈定异常(李随民等，2007)，最后转入MapGIS平台下进行成图，这样可方便与矿点图层叠加，结果如图4所示。趋势面法针对庞西垌地区这样的大范围海量数据，圈定效果并不理想，圈出的异常太少，突出了高频信息的同时过度压制了低频信息，使一些弱异常被忽视。而矿点往往出现在弱异常集中的地区，所以趋势面法不适用于本研究区。

图4 趋势面法圈定庞西垌地区Au、Ag元素异常示意图

4 分形方法圈定地球化学异常

分形最早由Mandelbrot于20世纪70年代提出，被描述为具有严格自相似结构的几何物体。分形的本质是标度不变性或自相似性，即在任何标度下物体的性质不变，是受所谓的幂律关系控制的。许多地质现象具有标度不变的特征，如岩石碎片、断层、地震、火山喷发矿藏、油井等，这些现象的频度和大小分布具有尺度不变性。国内外学者的研究表明，区域地球化学场十分粗糙，并非处处可微，数据服从分形分布。

含量-面积法是逼近地球化学异常的一种分形方法，Qiuming等(1994)认为地球化学背景值和异常值具有各自独立的幂指数关系，并提出确定地球化学异常的含量-面积分形方法。

设分形模型

N(r)=Cr-Dr＞0 (1)式中，r为特征尺度;C＞0称为比例常数;D＞0称为一般分维数;N(r)=N(≥r)表示尺度大于等于r的数目或和数。

笔者在MapGIS平台上实现含量-面积分形方法(陈玉香，2006;郭科等，2006;李宾等，2011)，基于含量与面积的幂律关系来确定研究区Au、Ag元素的异常下限值。首先在MapGIS平台上采用稠密数据高斯距离权法网格化，形成等值线图，然后利用分形求和法(申维，2007)借助于MapGIS的空间分析功能统计不同含量r值所对应的累计面积N(r)值，即元素含量大于等于r的面积。两边取自然对数，化为一元线性回归模型，应用最小二乘法回归各段直线，用最优化方法确定分界点，求出分维数D。最后对回归方程的显著性进行检验，通过显著性检验的分维数D对应的r值即为异常下限值(陈玉香，2006)。

研究区Au、Ag两种元素的分段拟合见图5。

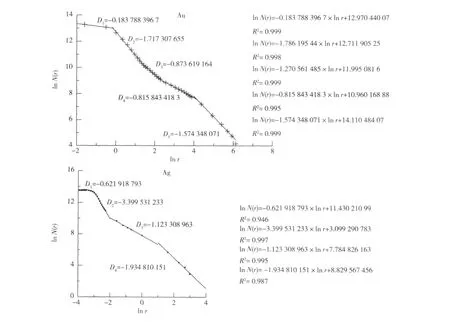
图5 庞西垌地区Au、Ag元素含量-面积关系图及拟合方程

Au、Ag元素各段拟合方程均通过显著性检验。根据图5可以看出，Au、Ag元素的含量与面积呈幂律关系，元素含量的空间分布是一种具有2个或2个以上标度的多重分形分布。本研究区中Au元素明显呈现5个无标度区，可得到4个相应的分界点，即4个异常下限理论值，分别为0.8、3.5、10.0、70.0 mg/t;Ag 元素则明显表现出4个无标度区，即可得到相应的3个分界点，即3个异常下限理论值，分别为 0.055、0.1、5.0 g/t。

根据得到的异常下限理论值，可作出对应元素的异常图(图6)。从分形方法圈定的庞西垌地区Au、Ag元素异常图可以看出，分形方法利用含量-面积统计量根据元素含量的内在分布特征来计算元素含量的异常下限理论值，既考虑了元素含量的内在富集规律，又考虑了元素含量分布的空间性;既突出了高频异常，又不压制低频信息的表现。异常下限分级按照元素内部的富集程度而定，易于突出强异常，同时有利于弱异常的表现，反映了整个区域的异常变化特征。该方法圈定的异常与已知矿点的吻合度最好。

图6 含量-面积法圈定庞西垌地区Au、Ag元素异常示意图

5 结论

通过对庞西垌地区Au、Ag元素含量分别利用传统方法、趋势面法、分形方法进行异常下限计算，进而圈定异常，并与已知矿点进行叠加分析。研究结果表明：(1)传统方法(迭代剔除法)在计算过程中剔除了大量的强异常信息，这在一定程度上削弱了高异常信息的表现，由于异常下限常取计算出的下限值及其2、4、8倍作为颜色梯度，计算过程较为机械，只考虑了元素含量的统计特征，忽视了元素含量本身的富集规律及其空间性。(2)趋势面法不适用于本研究区大范围海量数据的表达，在计算趋势面过程中，残差受数据范围的影响，圈定的异常太少，不能反映研究区的元素含量变化。(3)分形方法以无损地球化学数据完整性为前提，最能表现本研究区的元素含量变化规律，既突出了强异常，又利于弱异常的充分表现。异常下限不是机械的设定，而是通过计算元素含量-面积双对数图，来分析元素含量的富集规律，以此为依据计算异常下限理论值，更能表现元素含量的内在富集规律。

从圈定出的异常与已知矿点的吻合程度看，吻合度最好的是分形方法，其次为传统方法，最后为趋势面法。

通过对3种方法的对比可以看出，分形方法既考虑了元素的统计规律，又考虑了元素的内部富集规律和空间性，相对于其他两种方法具有明显的优势。

陈建国，夏庆霖.1999.利用小波分析提取深层次物化探异常信息［J］.地球科学：中国地质大学学报，24(5)：509-512.

陈玉香.2006.GIS技术——分形方法在化探数据处理中的应用探讨［D］.北京：中国地质大学.

陈志军.2007.多重分形局部奇异性分析方法及其在矿产资源信息提取中的应用［D］.武汉：中国地质大学.

郭科，魏友华，陈聆，等.2006.基于MapGIS平台下分形理论在地球化学异常圈定中的应用［J］.成都理工大学学报：自然科学版，33(4)：356-359.

韩东昱，龚庆杰，向运川.2004.区域化探数据处理的几种分形方法［J］.地质通报，23(7)：714-719.

纪宏金，林瑞庆，周永昶.2001.关于若干化探数据处理方法的讨论［J］.地质与勘探，37(4)：56-59.

李长江，麻士华.1999.矿产勘查中的分形、混沌与ANN［M］.北京：地质出版社.

雷丽，王绪本，倪师军，等.2000.小波分析在化探异常处理中的试验研究——以四川石棉田湾矿区为例［J］.矿物岩石，(3)：91-94.

李随民，姚书振，韩玉丑.2007.Surfer软件中利用趋势面方法圈定化探异常［J］.地质与勘探，43(2)：72-75.

李宗敏，申维.2008.基于奇异值分解法的含量-面积法对化探异常的确定［J］.地质通报，(5)：662-667.

李宾，李随民，梁玉明，等.2011.分形方法圈定河北省龙关地区化探元素异常［J］.地质调查与研究，34(2)：154-160.

任印国，魏永强.2006.使用Surfer软件绘制地质图件和处理地质数据的方法［J］.测绘技术装备，8(1)：34-36.

申维.1999.多维自仿射分布及其在地球化学中的应用［J］.高校地质学报，5(1)：59-65.

苏金明.2004.统计软件SPSS 12.0 for Windows应用及开发指南［M］.北京：电子工业出版社.

申维.2007.分形求和法及其在地球化学数据分组中的应用［J］.物探化探计算技术，29(2)：134-137.

孙忠军.2007.矿产勘查中化探异常下限的多重分形计算方法［J］.物探化探计算技术，29(1)：54-57.

王崇云.1987.地球化学找矿基础［M］.北京：地质出版社.

谢学锦.2002.面向21世纪的应用地球化学：谢学锦院士从事地球化学研究50周年［M］.北京：地质出版社.

於崇文.1999.大型矿床和成矿区(带)在混沌边缘［J］.地学前缘，6(2)：195-217.

赵鹏大.2004.定量地学方法及应用［M］.北京：高等教育出版社.

GOVTT G J S，GOODFELLOW W D，CHAPMAN R P，et al.1975.Exploration geochemistry distribution of elements and recognition of anomalies［J］.Mathematical Geology，7(5/6)：415-446.

MIESCHAT.1981.Estination of geochemical threshold and its statistical significance［J］.Geochemical Exploraion，16(1)：49-76.

QIUMING C，AFTERBERG F P，BALLANTYNE S B.1994.The separation of geochemical anomalies from background by fractal methods［J］.Journal of Geochemical Exploration，51(2)：109-130.

QIUMING C，AGTERBERG F P，BONHAM-CARTER G F.1996.A spatial analysis method for geochemical anomaly separation［J］.Journal of Geochemical Exploration，56(3)：183-195.

Discussions on anomaly delineation method of geochemistry in Pangxidong area

WANG Kun1，2，3，ZHOU Yong-zhang1，2，3，GAO Le1，2，3

(1.Department of Earth Sciences，Sun Yat-sen University，Guangzhou 510275，China;2.Guangdong Provincial Key Laboratory of Geological Processes and Mineral Resources Exploration，Guangzhou 510275，China;3.Center for Earth Environment and Resources，Sun Yat-sen University，Guangzhou 510275，China)

Pangxidong area was located in the south section of Qin-hang metallogenic belt and was the major metallogenic zones of precious metals and nonferrous metals.The tectonic structures were complicated and magma activity frequent.Based on the stream sediment survey data in Pangxidong area，the content of Au and Ag elements were taken as examples，their lower limit values were calculated and anomalies were delineated with conventional statistical method，trend surface analysis and fractal method.Through contrast of calculation course and application effect，the most appropriate method was explored for the delineation of geochemical anomaly under complicated geological settings.

Geochemical anomaly;Fractal method;Iterative method;Trend surface analysis;Pangxidong area;Guangdong and Guangxi

P618

A

1674-3636(2012)01-0064-06

2012-01-06;编辑：陆李萍

中国地质调查局地质矿产调查评价专项项目“广东庞西垌地区矿产远景调查(1212010071012)”资助

王琨(1985— )，女，硕士研究生，研究领域为综合地质异常提取及成矿预测，E-mail：wkun1111@126.com

10.3969/j.issn.1674-3636.2012.01.64