时滞神经网络对于新的二次优化的应用
2012-01-05张静文刘德友吴文娟
张静文, 刘德友, 吴文娟
(燕山大学 理学院 河北 秦皇岛 066004)
0 引言
常见的二次优化问题
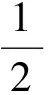
(1)
其中,M∈Rm×n,a∈Rn,Ω是一个凸集.二次优化问题在社会科学及工程中具有广泛的应用,其中包括回归分析、图像和信号处理、参数估计、滤波器设计、机器人控制等等.当M是正定矩阵时,式(1)为严格凸二次优化问题;当M是半正定矩阵时,式(1)为退化的凸二次优化问题.在很多情况下,矩阵M是不精确已知的,可能包含在一段区间上,这样的问题被称为区间二次优化问题.在许多实际应用中,最优化问题还有一个自然时变亟待解决.目前,主要利用神经网络技术实现优化方法,在运行时间程度上远远超过最受欢迎的数字计算算法.最近,有一些投影神经网络技术实现了解决此二次优化问题.文献[1]给出了最初的神经网络,解决了严格凸二次优化问题.为了克服处罚参数,当Ω是一个有界闭集时,文献[2]提出了投影神经网络技术,解决了严格凸二次规划和它的二元性,并得出全局指数稳定.文献[3-4]提出时滞投影神经网络,解决了二次优化问题,当Ω是一个无界闭集时,分析了该神经网络全局渐近稳定和指数稳定性.文献[5]提出了时滞神经网络对于线性投影方程解的分析及其应用,得出二次优化最优解新的充分条件.文献[6]又对非线性时滞细胞神经网络稳定性进行了分析,文献[7]给出了一种改进的进化神经网络优化设计方法.在此基础上,本文进一步把正定矩阵推广到广义正定矩阵,利用时滞神经网络模型和Lyapunov函数的特性,给出判断这种特殊二次优化最优解的充分条件.
1 模型及预备知识
根据[8-12]的方法,考虑时滞神经网络模型
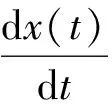
(2)
其中,τ≥0表示传输延迟,α是大于零的常量,M∈Rn×n给出线性映射方程[13]PΩ(u-α(Au+q))=u,其中α是大于零的常量,A是n维矩阵,q∈Rn,
Ω={u∈Rn|di≤ui≤hi,i∈S},S⊂L,L={1,2,…,n},
PΩ:Rn→Ω表示从Rn到Ω的映射影,并且有
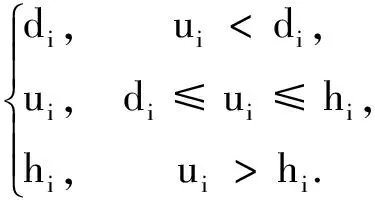
引理1投影算子PΩ满足不等式[14](x-PΩ(x))T(PΩ(x)-z))≥0,∀z∈Ω,x∈Rn.
引理2∀x,y∈Rn,投影算子PΩ满足不等式
(PΩ(x)-PΩ(y))T(x-y)≥(PΩ(x)-PΩ(y))T(PΩ(x)-PΩ(y)).
引理3A∈Rn×n,对∀0≠x∈Rn×1,都有可逆实对称矩阵S,使得xTSAx>0,则称A是广义正定矩阵.
引理4对每一个φ(t)∈CC([-τ,0])在整个时间区间[0,∞),(2)式存在一个唯一的连续解u(t).
定理1时滞神经网络模型(2)式全局指数稳定和渐近稳定[15],当I-αM是非退化的.
因此,时滞神经网络模型可以确保线性投影方程有解,并能够解决一类新的二次优化问题.
2 二次优化问题的应用
考虑二次优化问题
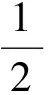
(3)
其中,M∈Rn×n,a∈Rn,M是一个对称的广义正阵,
Ω={x∈Rn|d≤x≤h},x=(x1,x2,…xn)T.
根据文献[8-12]的结论,为了解决此二次优化问题,提出时滞神经网络模型
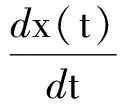
其中τ≥0表示传输延迟,α是大于零的常量,M∈Rn×n,M是一个对称的广义正定矩阵,并且满足I-αM是非退化的.假设对于二次优化问题的解是一个非空集合,若x*是(3)的最优解,当且仅当x*满足变分不等式
(x-x*)T(Mx*+a)≥0,x*∈Ω,∀x∈Ω.
(4)
此外,x*是(3)的最优解当且仅当对∀α≥0,u*是G(x)的一个零点映射,
G(x)=PΩ(x-α(Mx+a))-x.
为了得出(3)的最优解,借助时滞神经网络模型,
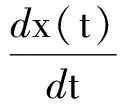
(5)
显然,(5)的平衡点对应于(4)的最优解.根据文献[16]的结论,就能借助时滞神经网络模型(5)来解决最优化问题(3).可构造一个新的Lyapunov函数来证明系统(5)是全局收敛的.
定理2时滞神经网络(5)全局稳定于二次优化(3)的解,当矩阵M是一个对称的广义正定矩阵.
证明假设x*是(5)的平衡点,考虑Lyapunov函数,
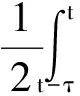
其中I是n维的单位向量.根据引理3,一定存在可逆的实对称矩阵D使得xTDMx>0,并且
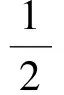
其中,<·,·>表示内积.
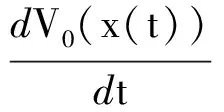
α
=α x*,PX[x(t)-α(Mx(t)+a)]-x(t)>+ (6) α =α α(Mx(t)+a)]-x*>+α (7) α =<αf′(x)-x(t)+PX[x(t)-α(Mx(t)+a)],PX[x(t)-α(Mx(t)+a)]-x*>+ =α x*>+ x(t)>+ (8) 结合(4),(6)~(8)和引理1,得 αDM+I是对称的正定矩阵,所以存在对称矩阵A,使得 αDM+I=A2. A(x(t-τ)-x*))T×(A(x(t)-x*)-A(x(t-τ)-x*)) =-‖x(t)-PX[x(t)-α(Mx(t)+a)]‖2- =-‖x(t)-PX[x(t)-α(Mx(t)+a)]‖2- ≤0. (9) V(xt)是系统(5)的Lyapunov函数.通过引理4,系统(5)的最大区间解为[0,∞).由压缩不变原理[17],一定存在常数τ,有xt→E∩V-1(τ),t→∞,其中E包含在最大不变集S中,S={xt|dv/dt=0}.通过(9)和定义V(xt),有dv/dt=0,当且仅当dx/dt=0,即E∩{x∈Ω|dx/dt=0},则动力系统(5)全局收敛于平衡点,即为不定二次优化(3)的最优解. 通过实例验证二次优化解的有效性. 例题1考虑二次优化问题 (10) 其最优解为x*=[-1 1-1]T,则给出时滞神经网络模型(11)式解决二次优化问题, (11) x(t)的初始值区间为[-1,0].通过定理2,则有系统(11)是全局收敛于平衡点x*,即(10)的最优解. 借助时滞神经网络解线性映射方程的模型,证明一种新的二次优化问题,把优化问题更进一步推广.且通过数值例子,验证了本文结果的有效性. [1] Kennedy M P,Chual L O.Neural networks for nonlinear programming[J].Circuits and Systems,1998,35(5): 554-562. [2] Xia Yousheng,Feng Gang,Wang Jun.A recurrent neural network with exponential convergence for solving convex quadratic program and related linear piece wise equations[J].Neural Networks,2004,15(7):1003-1015 . [3] Yang Yongqing,Cao Jinde.Solving quadratic programming problems by delayed projection neural network[J].Neural Networks,2006,17(2): 1630-1634. [4] Yang Yongqing,Cao Jinde.A delayed neural network method for solving convex optimization problems[J].Int J Neural Syst,2006,16(4):295-303. [5] Cao Jinde.A delayed novel neural network for solving linear projection equations and its analysis[J].Neural Networks,2005,16(4):834-843. [6] 李洁坤,丁明智,虞继敏.非线性时滞细胞神经网络稳定性分析[J].郑州大学学报:理学版,2010,42(3): 54-58. [7] 杨华芬,杨有,尚晋.一种改进的进化神经网络优化设计方法[J].郑州大学学报:工学版,2010,31(5):116-120. [8] Cao Jinde,Wang Jun.Exponential stability and periodic oscillatory solution in BAM network with delays[J].Neural Networks,2002,13(2):457-463. [9] Cao Jinde.A exponential stability of recurrent neural networks with Lipschitz continuous activation functions and time delays[J].Neural Networks,2004,15(2):379-390. [10] Xia Yousheng,Wang Jun.A general projection neural network for solving monotone variational inequalities and rlated optimization problems[J].Neural Networks,2004,15(2):318-328. [11] Xia Yousheng.A new neural network for solving linear and quadratic programming problems[J].Neural Networks,1996,7(2):1544-1547. [12] Xia Yousheng,Wang Jun.A general projection neural network for solving monotone variational inequalities and related optimization problems[J].Neural Networks,2001,12(2):251-260. [13] Xia Yousheng,Wang Jun.A recurrent neural networks for solving linear projection equations[J].Neural Networks,2000,11(2): 337-350. [14] Kinder D,Stampcchia G.An introduction to variational inequalities and applications[J].Academic,1980,6(2):121-125. [15] Hale J K,Verduyn Lunel S M.Theory of Functional Differential Equation[M].New York:Springer-Verlag,1977:84-89. [16] Liu Qingshan,Cao Jinde ,Xia Yousheng.A delayed neural network for solving linear projection equations and its analysis[J].Neural Networks,2006,17(2):1045-1055. [17] Lasalle J P.The stability of dynamical systems[C]//CBMS-NSF Regional Conference Series in Applied Mathematics.Philadelphia,1976,3(2):62-66.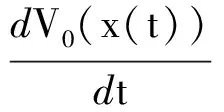
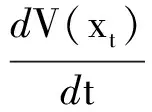
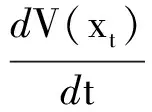
3 仿真实例

4 结束语
