信息不对称条件下的成矿信息集成方法

樊俊昌，毛先成，邹品娟，曹 芳，胡 超，张宝一

(1. 中南大学 有色金属成矿预测教育部重点实验室，长沙 410083；2. 中南大学 地球科学与信息物理学院，长沙 410083；3. 山金西部地质矿产勘查有限公司，西宁 810016)

成矿信息集成或融合是指在全面研究和综合分析地质、地球物理、地球化学和遥感资料的基础上，总结成矿规律及控矿因素，从中提取出指示矿床存在、赋存规模及质量的评价信息，为矿产资源预测评价，制订普查找矿的最佳方案提供依据[1−2]。作为矿产资源GIS评价的基础[3]，成矿信息融合技术日益受到国内外学者的重视，如采用回归模型进行地质信息集成并对矿产资源预测评价，取得了较好的效果[4]。此外，许多地质学家进行了大量的成矿信息集成应用研究[5−6]。经过多年研究实践，已逐步发展完善。然而，在成矿信息提取与综合(集成)过程中发现一些技术难题，如成矿信息提取不充分[5−9]、信息不对称等[8−10]，严重影响了矿产资源定量评价的效果。针对成矿信息提取不充分，特别是地质信息提取不充分的问题，可采用成矿信息场分析方法[11]解决。本文作者针对找矿信息不对称的问题，以桂西—滇东南地区锰矿为研究实例，提出一种新的成矿信息集成方法，即组合作用域信息集成方法，并按此思路利用线性回归模型[12]建立组合作用域信息集成预测模型。该建模方法摒弃了传统预测模型的单一作用域观点，采用根据地质变量作用域的不同组合，分别建立各自预测模型的回归方程的方法进行预测，从而解决目前找矿信息不对称的问题。

1 组合作用域信息集成方法

找矿信息不对称(不对等)问题，是当前矿产资源定量评价面临的技术难题。找矿信息在模型区(已知区)和预测区(未知区)具有不对称的特点，为了解决该问题，以地质信息(地质变量)的组合作用域为集成范围(建模域)建立集成模型，该模型称为组合作用域集成模型，这些模型由于建模域的不同，可以是地质变量的各种组合。对预测单元进行估值时，选取的信息集成预测模型的变量组合应与预测单元的变量组合相一致(对等)。

1.1 组合作用域的概念

所谓作用域，是指地质信息或地质变量的空间分布范围。地质变量作用域的确定需综合考虑下述3种情况：

1) 由数据分布范围定义作用域。例如，某地层等厚线，由于工作程度的差异，只在一定范围可以获取到某地层等厚线数据，而在区域外采用空间外推方法又难以准确模拟，则该范围即为某地层等厚线变量的作用域。

2) 由地质变量的影响范围确定作用域。例如，同沉积断裂的影响范围是有限的，超过一定的影响范围，该断裂就没有影响了，这时该范围即为同沉积断裂成矿影响场的作用域；

3) 由地质变量在模型区值域(min，max)确定预测区的作用域。例如，沉积盆地距离场在模型区内的值域是[0, 100 km]，在这个值域内，资源量与沉积盆地距离场呈现某种关联关系，而当距离场值远超过该值域时，这种关联关系很有可能不再存在，为保证模型的可靠性，将地质变量在预测区的作用域限定为地质变量取值符合该值域时的分布范围。

在实际计算时，可通过对上述3种情况得到的作用域求交而获得地质变量的作用域。因此，组合作用域是指多个地质变量组合的空间分布范围，即多个地质变量的作用域的交集。

1.2 组合作用域集成模型

已知n个变量X1，X2，…，Xn，其作用域分别为D1，D2，…，Dn。模型区为DM，预测区为DP。D1，D2， …，Dn在模型区DM中的单元数分别为N1, N2, …,Nn，则对于各种作用域组合可以建立集成模型。

1) 单元集成模型

若对于某一个变量 Xi作用域对应的Ni≥N0(N0设定为30)，则变量Xi的作用域Di位于模型区中的单元可以参与建模，如图1所示。模型称为M(i)，变量组合为(Xi)。

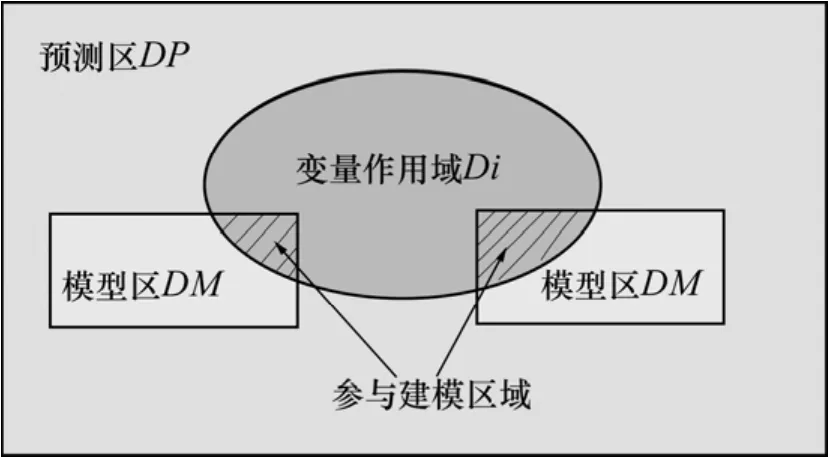
图1 单元集成模型建模示意图Fig. 1 Modeling for cell integrated model

2) 二元集成模型

若变量 Xi，Xj的作用域 Di，Dj的交集 Di∩Dj在模型区中单元数 Nij≥N0(N0设定为 30)，则变量 Xi，Xj的作用域Di，Dj的交集Di∩Dj位于模型区中的单元参与建模，如图2所示。模型称为M(i, j)，变量组合为(Xi, Xj)。

3) 多元集成模型

若变量 X1，X2，…，Xp的作用域 D1，D2，…，Dp的交集 D1∩D2∩…∩Dp在模型区中的单元数为N12…p≥N0(N0设定为 30)，则变量 X1，X2，…，Xp的作用域 D1，D2，…，Dp的交集位于模型区中的单元参与建模。模型称为M(1，2，…，p)，变量组合为(X1，X2，…，Xp)。

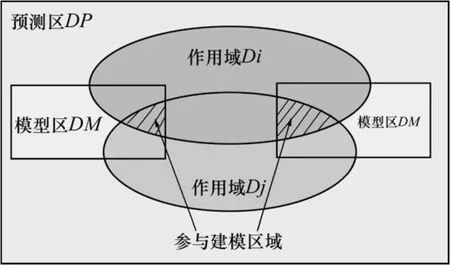
图2 二元集成模型建模示意图Fig. 2 Modeling for integrated model of two-variables

依次递推可以得到所有模型，模型或变量组合的最大个数为：

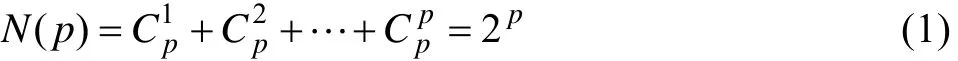
1.3 组合作用域集成线性回归模型

线性回归模型是矿产资源定量评价中最常用的预测模型，本文根据上述组合作用域的思路，提出了组合作用域集成线性回归模型。采用组合作用域线性回归模型建立矿产量预测模型的基本步骤为：

第一步，对地质变量Xi与资源量Y进行一元线性回归分析，如存在相关关系，转到第三步，否则进入第二步；

第二步，对地质变量 Xi进行变换得到地质变量Xi′，对变换后的地质变量 Xi′与资源量Y进行一元线性回归分析，如存在相关关系，转到第三步，否则舍弃该地质变量Xi和转换后的地质变量 Xi′；

第三步，对所有与资源量Y存在相关关系的地质变量 Xi(或转换后的地质变量 Xi′)组合进行多元(二元到p元)线性回归分析，组合时要考虑地质变量的作用域在模型区范围内是否有交集(否则变量不能进行组合)，若资源量与变量组合存在相关关系，则得到其线性回归方程，否则舍弃该变量组合；

第四步，对每个单元格，选取合适的多元变量组合(一元到p元)线性回归方程，得到其预测资源量。

1) 组合作用域集成一元线性回归分析

组合作用域集成一元线性回归分析是组合作用集成线性回归分析的关键。在组合作用域集成一元线性回归分析中通过对模型区的抽样，检验地质变量(或转换后的地质变量)与资源量之间是否存在线性相关关系，只有这些检验通过的地质变量(或转换后的地质变量)才参与后续的组合多元线性回归分析。另外，通过对地质变量(或转换后的地质变量)在模型区内值域范围(min，max)的限定，进一步修正了变量的作用域范围，为在预测中采用正确的线性回归方程奠定了基础。

组合作用域集成一元线性回归分析不要求地质变量的数据范围(数据范围外统一设置为无效值−9 999)覆盖这个模型区，只需覆盖部分模型区，抽样统计时只抽取模型区内的有效数据。组合作用域集成一元线性回归分析的流程如图3所示。

2) 组合作用域集成多元线性回归分析

则D(X1，X2，…，Xp)与模型区DM的交集为

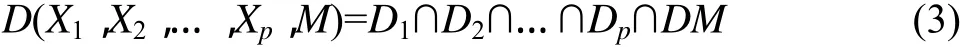
若D(X1，X2，…，Xp，M)中单元数目满足抽样统计要求，则可以检验资源量Y与地质变量X1，X2，…，Xp之间的线性相关关系，如检验通过，则建立资源量Y与地质变量X1，X2，…，Xp的线性回归方程。组合作用于集成多元现行回归分析的流程如图4所示。

采用该方法可得最多变量组合线性回归方程个数为N(p)，计算见式(1)。实际求解过程中，由于众多变量组合不能通过回归效果显著性检验，所得的模型的个数要远远小于N(p)。

2 应用实例

本文以桂西—滇东南地区为例，以桂西—滇东南多元地学空间数据库[13]为基础，利用组合作用域集成线性回归模型，对桂西—滇东南地区锰矿进行成矿预测，并生成了矿产资源量预测值图。

2.1 研究区成矿地质背景

研究区涵盖广西、云南、贵州三省部分地区，地理坐标为东经 103°30′～107°30′，北纬 22°40′～26°30′，覆盖区域面积约40 000 km2。该地区是我国重要的锰矿集中区[14]，已发现锰矿床(点)241处，有亚洲最大锰矿—广西下雷超大型锰矿[15]。因此，对该区域进行锰矿勘查具有非常好的找矿前景。

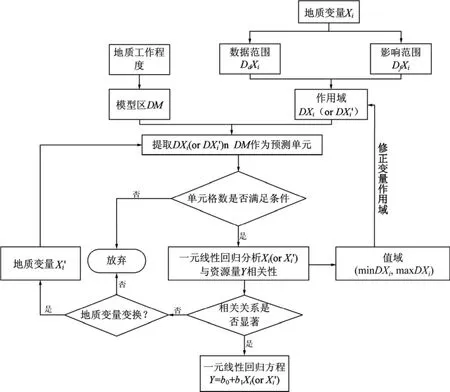
图3 组合作用域一元线性回归分析流程图Fig. 3 Flow chart for unary linear regression analysis under combination domains

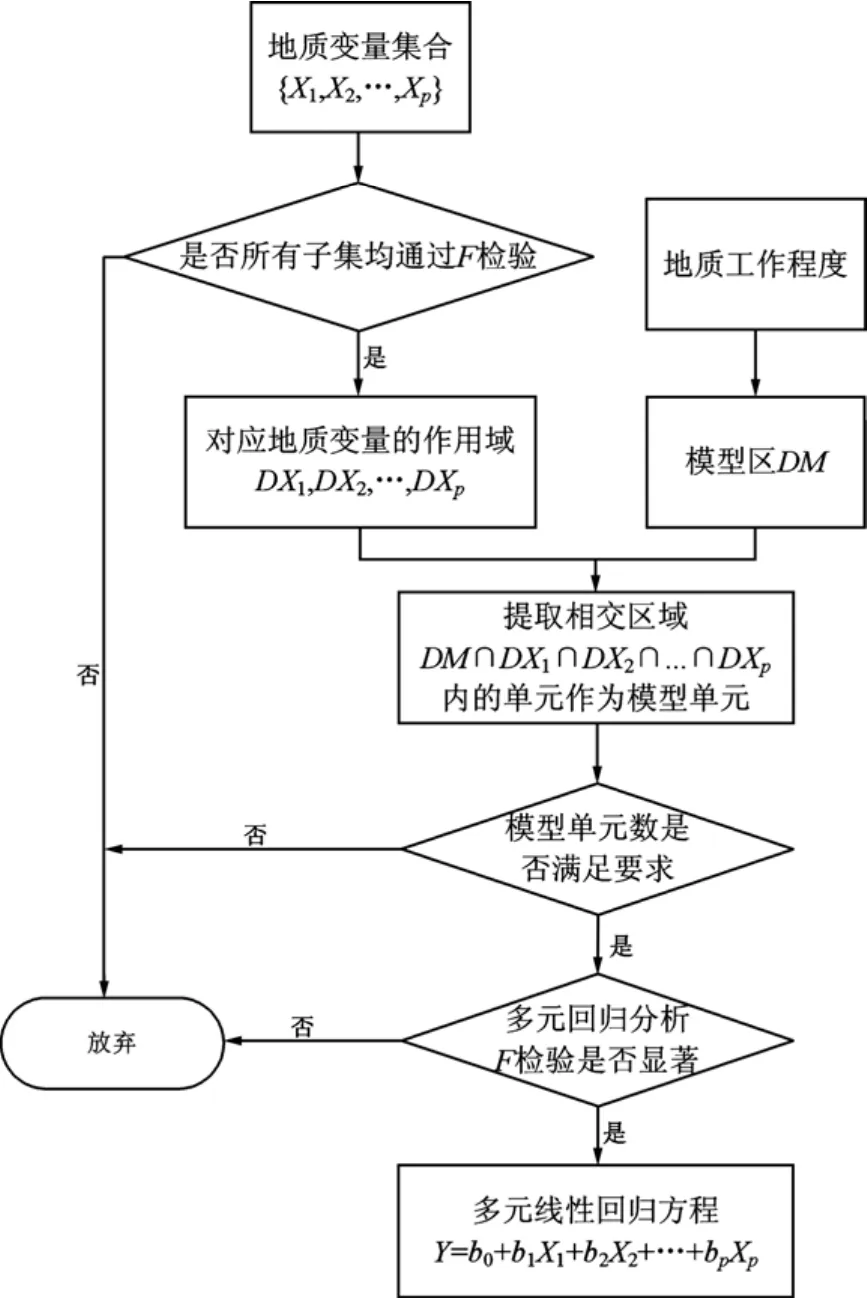
图4 组合作用域多元线性回归分析流程图Fig. 4 Flow chart for multiple linear regression analysis under combination domains

2.2 组合作用域信息集成预测模型

通过区域成矿规律总结可知，桂西—滇东南地区的主要成矿信息包括地层时代及层位、沉积断裂、沉积盆地、沉积相分布、岩性组合分布、地层厚度、地形和航磁异常等。采用成矿信息场分析方法，对上述成矿信息进行提取，可得到桂西—滇东南地区的锰矿成矿预测评价指标集。经研究可知，矿化分布与预测评价指标集之间存在着一定的关联，这种关联可以通过映射模型(如线性回归模型)来表达。利用这种映射模型，通过预测评价指标集计算出研究区各个单元的矿化指标，从而可以估算出研究区的锰矿资源量。

考虑到模型区和预测区的找矿信息不对称问题，采用组合作用域集成线性回归模型，建立研究区锰矿预测评价指标集到矿化指标的映射模型，该模型称为锰矿资源量预测模型。

在仿真过程中，测速电机永磁转子以100步为单位在恒速和匀加/减速状态中交替切换，采用蒙特卡洛方法仿真500 ms，仿真结果见图5至图7。从图5可以看出，仿真所得感应电动势的正弦曲线能够较好地跟踪实际测速电机模型输出的电动势曲线。由于仿真时是基于单一的恒速模型运行自适应降阶无迹卡尔曼滤波算法，从图6和图7中可以看出单模无迹卡尔曼滤波算法在测速电机永磁转子恒速状态下的估计精度较高，而在加速状态下的估计精度较低。

在利用线性回归分析建立预测模型之前，由于矿化指标与预测评价指标集之间的关联关系是非线性的，所以，需要对预测评价指标进行非线性变换。以晚泥盆世活动断裂影响场地质变量的变换为例，其变换方程为

式中：fF_D3为晚泥盆世活动断裂影响场地质变量，fF_D3_T为fF_D3经变换后的地质变量。只有当模型通过回归效果F检验时，才认为具有显著的回归效果。在实际求解过程中，回归效果显著的模型才能列为资源量预测的候选模型，但模型的数目仍然很庞大，在此仅给出一元线性回归模型(见表1)。

在对每个单元进行锰矿资源量预测时，为保证找矿信息的对等性，需要检验其是否位于地质变量的组合作用域内，只有该单元所在的组合作用域对应的回归模型才能作为资源量预测的候选模型。当某个单元具有多个候选模型时，采用下面两个准则进行候选模型的优选。

准则 1：变量组合元数优先原则，选取尽可能多的地质变量组合建立的回归方程进行预测；

准则 2：F检验值优先原则，在回归方程元数相同条件下，取F检验值最大的回归方程进行预测。

利用上述两个准则，可以筛选出最优的多作用域线性回归模型，该最优模型即为该单元的预测模型。

利用上述方法，对研究区的每个单元进行预测模型的优选，凡能选择到预测模型的单元，都可利用其选择出的预测模型进行资源量的估值预测。对整个研究区的锰矿资源量的估值预测结果如图5所示。

结合已有的多元锰矿地学空间数据库和岩相古地理数据，并参照桂西—滇东南锰矿资源量预测值分布图，圈定桂西—滇东南地区的锰矿预测远景区7个(见图6)，并将其划分为3个等级。

Ⅰ类：成矿条件十分有利，预测依据充分，成矿匹配程度高，可建议优先安排勘查工作的地区。

Ⅱ类：成矿条件有利，有预测依据，成矿匹配程度较高。

Ⅲ类：具成矿条件，可作为探索的地区，或现有矿区外围和深部，有预测依据，据目前资料认为资源潜力较小的地区。

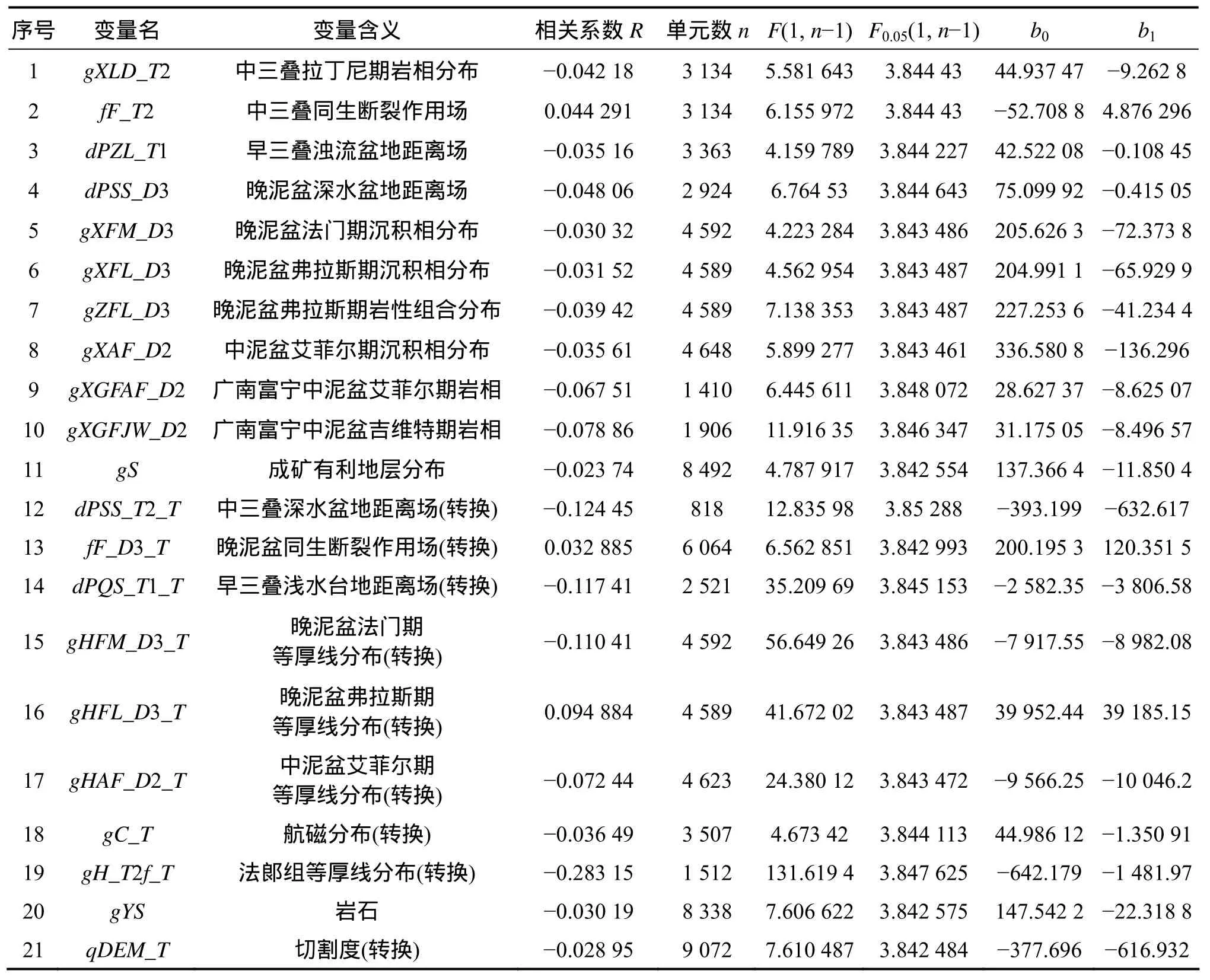
表1 组合作用域一元线性回归模型Table 1 Unary linear regression models under combination domains

图5 桂西—滇东南地区锰矿资源量预测值分布图Fig. 5 Estimation of manganese ore in West Guangxi—Southeast Yunnan district

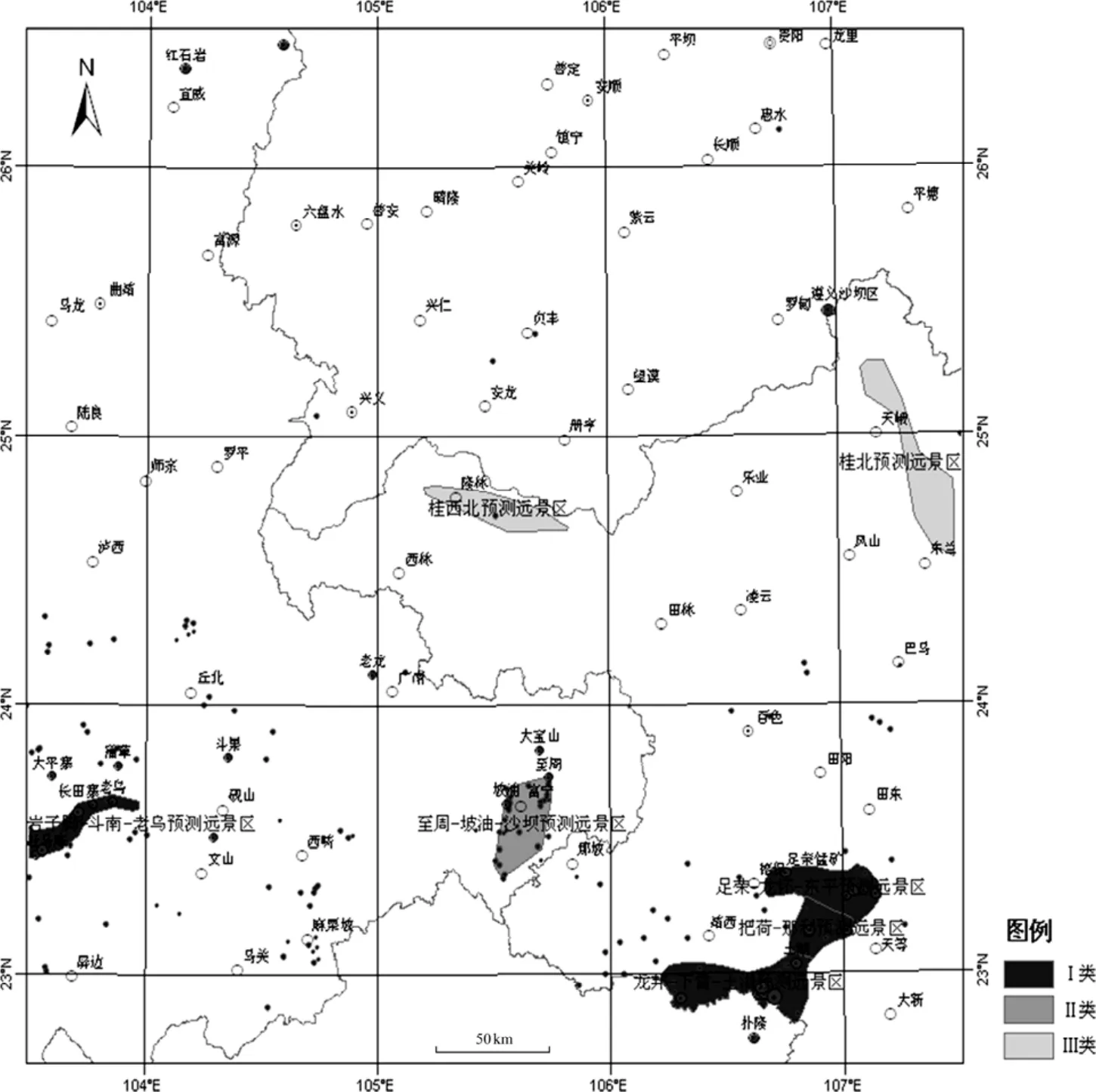
图6 桂西—滇东南地区锰矿预测远景区分布图Fig. 6 Prediction of manganese ore prospect areas in West Guangxi—Southeast Yunnan district

分析表明，已知中、大型锰矿床(点)大部分落入I、II级预测远景区，说明该方法对锰矿床(点)的预测没有漏判。同时，预测远景区分布走向与研究区内的控矿构造、地层分布基本一致，成矿作用明显受断裂及沉积盆地控制，这与研究区内已知锰矿床(点)特征吻合。总之，远景区的划分与该区域的成矿地质条件所反映的找矿前景基本一致，对该地区的进一步找矿具有一定的指示意义。

3 结论

1) 针对目前广泛存在的成矿信息不充分的问题，在回归模型方法的基础上，提出了一种多作用域组合模型，即组合作用域集成线性回归模型。该方法以地质变量的组合作用域为建模范围(建模域)建立预测模型，从而摈弃了传统预测模型的单一作用域观点。对预测单元进行资源量预测时，选取的预测模型的变量组合与预测单元的变量组合相一致(对等)，解决了成矿信息不对称的问题。

2) 以桂西—滇东南地区锰矿为例，采用成矿信息场分析方法提取了某些地质类的成矿信息，并建立了桂西—滇东南地区锰矿成矿预测指标集。考虑到模型区和预测区的找矿信息不对称问题，采用组合作用域线性回归分析，建立了研究区锰矿预测评价指标集到矿化指标的映射模型，即锰矿资源量预测模型，从而对研究区锰矿资源量进行定量预测。

3) 实例分析表明，采用组合作用域信息集成预测模型能精细、有效地对研究区中的锰矿资源量进行预测，其结果同时表明该方法的合理性和可靠性。利用组合作用域信息集成方法可帮助解决成矿信息不对称的问题。

[1] 肖克炎, 朱裕生, 张晓华, 宋国耀, 陈郑辉. 矿产资源评价中的成矿信息提取与综合技术[J]. 矿床地质, 1999, 18(4):379−384.

XIAO Ke-yan, ZHU Yu-sheng, ZHANG Xiao-hua, SONG Guo-yao, CHEN Zhen-hui. The extraction and integration technology of minerogenic information in mineral resources assessment [J]. Mineral Deposits, 1999, 18(4): 379−384.

[2] RANJBAR H, HASSANZADEH H, TORABI M, ILAGHI O.Integration and analysis of airborne geophysical data of the Darrehzar area, Kerman Province, Iran, using principal component analysis [J]. Journal of Applied Geophysics, 2001,48(5): 33−41.

[3] 肖克炎, 朱裕生, 宋国耀. 矿产资源GIS定量评价[J]. 中国地质, 2000, 27(7): 29−32.

XIAO Ke-yan, ZHU Yu-sheng, SONG Guo-yao. GIS quantitative evaluation of mineral resources [J]. Geology in China, 2000, 27(7): 29−32.

[4] CHUNG C F, AGTERBERG F P. Regression models for estimating mineral resources from geological map data [J].Mathematical Geology, 1980, 12(5): 473−488.

[5] LICHT O A B, TARVAINEN T. Multipurpose geochemical maps produced by integration of geochemical exploration data sets in The Parana Shield, Brazil [J]. Journal of Geochemical Exploration, 1996, 56(3): 167−182.

[6] CARRANZA E J M, Hale M, FAASSEN C. Selection of coherent deposit-type locations and their application in data-driven mineral prospectivity mapping [J]. Ore Geology Reviews, 2008, 33(3/4): 536−558.

[7] OTHNIEL K L, ELISHA M S, CHEO E S. The application of evidential belief functions in the integration of regional geochemical and geological data over the lfe-llesha goldfield,Nigeria [J]. Journal of African Earth Sciences, 1997, 25(3):491−501.

[8] LUO X, DIMITRAKOPOULOS R. Data-driven fuzzy analysis in quantitative mineral resource assessment [J]. Computers &Geosciences, 2003, 29: 3−13.

[9] CARRANZA E J M, SADEGHI M. Predictive mapping of prospectivity and quantitative estimation of undiscovered VMS deposits in Skellefte district (Sweden) [J]. Ore Geology Reviews,2010, 38(3): 219−241.

[10] 叶天竺, 肖克炎, 严光生. 矿床模型综合地质信息预测技术研究[J]. 地学前缘, 2007, 14(5): 11−19.

YE Tian-zhu, XIAO Ke-yan, YAN Guang-sheng. Methodology of deposit modeling and mineral resource potential assessment using integrated geological information [J]. Geoscience Frontiers,2007, 14(5): 11−19.

[11] 毛先成, 周尚国, 张宝一, 胡 超, 汪凡云, 曾文波. 基于场模型的成矿信息提取方法研究—以桂西−滇东南锰矿为例[J].地质与勘探, 2009, 45(6): 704−715.

MAO Xian-cheng, ZHOU Shang-guo, ZHANG Bao-yi, HU Chao,WANG Fan-yun, ZENG Wen-bo. Research on extraction of metallogenic information based on field model: A case of manganese ore in the Western Guangxi and Southeastern Yunnan areas [J]. Geology and Prospecting, 2009, 45(6): 704−715.

[12] 赵鹏大, 胡旺亮, 李紫金. 矿床统计预测(第二版)[M]. 北京:地质出版社, 1994: 113−115.

ZHAO Peng-da, HU Wang-liang, LI Zi-jin. Statistical prediction of mineral deposit [M]. Beijing: Geological Publishing House,1994: 113−115.

[13] 张宝一, 毛先成, 周尚国, 汪凡云, 曾文波, 闫 芳, 邓吉秋.矿产资源预测评价数据库的设计与实现—以桂西−滇东南锰矿为例[J]. 地质与勘探, 2009, 45(6): 697−703.

ZHANG Bao-yi, MAO Xian-cheng, ZHOU Shang-guo, WANG Fan-yun, ZENG Wen-bo, YAN Fang, DENG Ji-qiu. The design and implement of prediction and assessment for mineral resources database—In case of manganese deposit in the Western Guangxi and Southeastern Yunnan provinces [J].Geology and Exploration, 2009, 45(6): 697−703.

[14] 骆华宝. 我国优质锰矿的勘查方向[J]. 地质与勘探, 2002,38(4): 8−11.

LUO Hua-bao. The direction of prospecting for high quality manganese ore resources in China [J]. Geology and Exploration,2002, 38(4): 8−11.

[15] 董宝林, 张 鹏, 李振华. 广西锰矿资源现状及勘查开发建议[J]. 南方国土资源, 2006(1): 15−17.

DONG Bao-lin, ZHANG Peng, LI Zhen-hua. Manganese resource exploration and development status and proposed in Guangxi [J]. Land and Resources of Southern China, 2006(1):15−17.