一种快速分析周期性慢波结构色散特性的方法*
2012-01-03石成才
杨 阔,石成才
(1.电子科技大学物理电子学院,四川 成都 610054;2.阿坝师范高等专科学校电子信息工程系,四川 汶川 623000)
一种快速分析周期性慢波结构色散特性的方法*
杨 阔1,2,石成才1
(1.电子科技大学物理电子学院,四川 成都 610054;2.阿坝师范高等专科学校电子信息工程系,四川 汶川 623000)
分析了周期性慢波结构中的场分布特点,提出了一种利用粒子模拟软件Magic快速分析周期性慢波结构色散特性和描绘色散曲线的方法.以一个具体的慢波结构为实例,详细介绍这种方法的操作过程,并结合周期性慢波结构的场分布特点及其他电磁理论分析这种方法的原理,理论证明它的可行性.这种方法尽管有一定的误差,但是其操作简单而迅速,在进行一些微波电子器件的初步设计工作当中有一定的实际意义.
周期性慢波结构;色散特性;空间谐波;谐振
行波管和返波管是通过行波场与电子注相互作用从而放大微波信号或产生微波振荡的微波电真空器件,它们的高频系统属于慢波线型[1].具有正弦波纹内壁的中空周期性慢波结构是返波管中使用较多的一类慢波线.在进行返波管的设计工作时首先需要研究慢波结构的色散特性.
用冷腔测试的方法探究慢波结构的色散特性需要加工出实际物理器件进行复杂的电磁测试,其成本高、期限长[2].理论分析并数值求解色散特性往往只针对特定结构的慢波线,并且运算量较大,耗时较长.而利用电磁仿真软件进行建模并分析慢波结构的色散特性则简单而快速.Magic是一款成熟的粒子模拟软件,用这一程序分析慢波结构的色散特性效果比较好.
1 周期性慢波结构中的场分布和空间谐波
边界条件在轴向非均匀而周期性变化的慢波线称为周期性慢波结构.在返波管中常见的是内壁半径沿轴向按正弦规律发生变化的一类周期性慢波结构,其内壁半径可用表达式r=r0+hcos(2πz/L)来描述.其中:r0是平均半径;h是波纹深度;L是其空间周期长度.由于空间结构上的周期性,给定频率下在其中传输的某一模式的电磁波的分布也具有周期性,可用如下数学表达式来描述:

其中:φ是这个模式在某个场分量的幅值分布,对于无损耗系统;γ0=jβ0,这其实就是Floquet定理的数学表述[3],是分析周期性慢波结构的出发点.根据(1)式所反映的周期性,在无损耗周期性慢波结构中某一模式的某个场分量可以写成φ(r,r)e-jβ0L.
周期性函数都可展开成傅立叶级数的形式,则

由此可见,由于结构的空间周期性,周期性慢波结构中传播的某个模式的波可分解为无数个空间谐波.n次空间谐波的相位常数为

0次空间谐波又称为基波,其相位常数与这无穷多个空间谐波的合成波的相位相同.某些空间谐波的相位常数会出现负数,这表明它们的相速与合成波的群速方向相向,这些反向空间谐波称为返波,返波管正是利用其中的-1次反向空间谐波在慢波结构中形成反馈回路而产生微波振荡的[4].各个空间谐波的幅值之间的比例关系是确定的,由慢波系统的空间结构决定,所以,增强或减弱其中某一个空间谐波则整个模式的幅值就会得到相应的变化.整个场分布在时间上是简谐变化的,但是在空间上具有周期性而非简谐分布特点.由这种周期性和各空间谐波之间的相位关系不难发现,周期性慢波结构中某一特定模式的色散关系具有周期性[5],反映在图像上就是β-f曲线呈周期状.
2 用驻波法确定慢波结构中TM01模的有限个频率值与相位关系
采用一个具有正弦波纹内壁的中空轴对称慢波结构,其中:r0=15mm;h=2mm;L=16mm.用理想导体片封闭这段慢波结构的输入和输出端口,置入一个沿轴向(z向)的线电流源,在Magic中的函数表达式为J0*step(2*SYS$Dtime,t),其中J0为自己选取的电流密度值,SYS$Dtime是系统根据用户划分的网格和Courant条件计算的时间步长.这实际上相当于在谐振腔内引入一定频率范围内的噪声源,程序运行过程中会看到场分布是杂乱无章的.在Magic代码中书写测量此线电流源两端电压的语句并且进行傅立叶变换,程序运行完之后所得的频谱如图1所示.
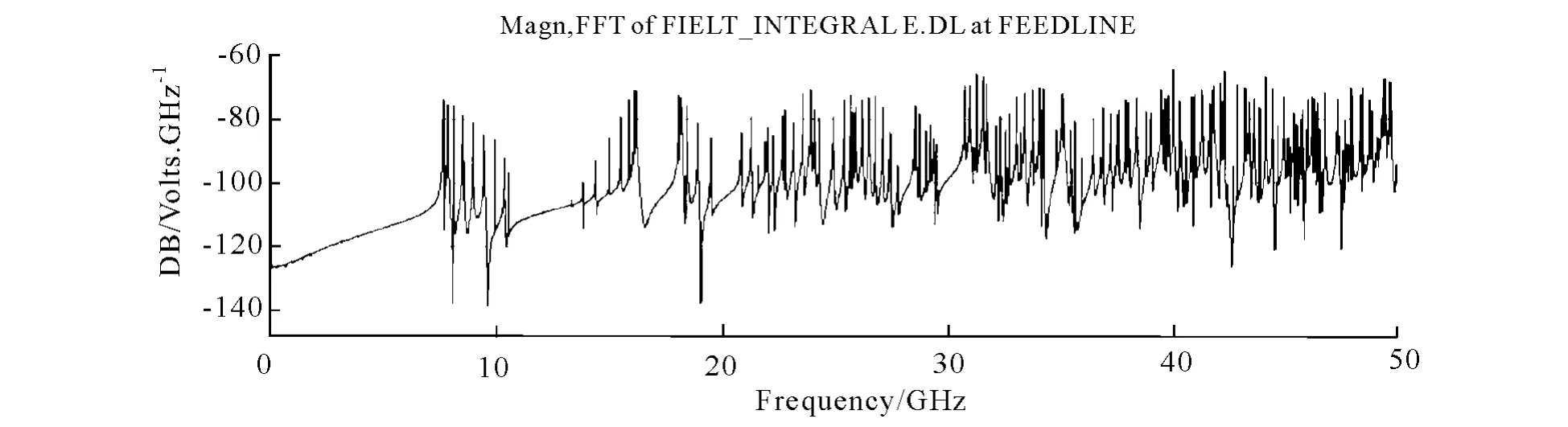
图1 腔体内谐振模式的傅立叶频谱图
这一频谱图所显示的是在一定的频率范围内(0~50Hz)所能谐振的频率点,每个分离的频率点对应一特定的振荡模式.因为激励源是一个沿轴向的电流源,所以谐振模式都是TM模.整个分布呈现不连续的片段,每个片段内各频率点同属于一个横向模式,最低一个片段对应的是一组最低横向模式TM01n,即角向无变化径向分布一个半驻波,轴向有n个半驻波的谐振模式.放大图1中所选定的一段频谱,共有10个频率点(表1).

表1 谐振频率与所对应的序号
根据图1中的序号可求出相应谐振模式的相位常数.比如,n=6时模式为TM016,即在轴向有6个半驻波数目,那么其相位常数,在Magic中很容易通过本征模命令验证这一点.在附近对相同的谐振腔进行eigenmode运算,Magic程序搜索到的谐振频率为10.553GHz,与上面所得结果之间的差异甚小,所得角向磁场分布如图2所示.

图2 第9个谐振模式场分布
由这一场分布图和其他几个场分量的分布图可知,这一谐振模在径向只有1个半驻波数,角向场无变化,沿轴向分布半驻波数目为9,因此它所对应的谐振模是TM019.
3 描绘出慢波结构中TM01模的色散特性曲线
去掉谐振腔两端的金属片后形成周期性慢波结构,可以通过以上的数据结果来描述这一结构的色散特性,实际上已经得到了慢波结构中TM01模式若干个频率值和对应的相位常数.先以(βn,fn)为坐标画出一段光滑曲线,相位常数范围从0~π/L,在谐振腔所对应的是离散的10个TM01n谐振模式,而在慢波结构中表明连续的频率值与相位的关系,其频率范围是7.600 1GHz~10.533GHz,也就是说这一频率范围内的电磁波能在这个慢波结构中以TM01模式传播.有必要分析处于这一范围两端的2个频率值,f0=7.600 1GHz的TM电磁波在谐振腔内的模式为TM010,场沿轴向没有发生变化,这在慢波结构中显然是截止的;f9=10.533GHz的TM电磁波在谐振腔内的模式为TM019,场沿轴向分布的半驻波数目为9,如图2所示.这一频率的电磁波进入慢波结构时由于所有不均匀性的反射波与入射波都将得到同相叠加形成全驻波,所以波同样被截止.慢波结构的周期数决定其每个横模允许存在纵向模式的数目,若慢波结构周期数目为n,则其纵向模式数目为n-1[6],所以上面的频率范围便是TM01模式的一个通带.既然TM01是这一结构的最低模式,那么这一频率范围也是它的第1个通频带.
对周期性慢波结构中场分布的理论分析可知,合成某一传输模式的无数个空间谐波具有相同的频率和共同的群速,而它们的相位常数如(2)式所示,其中基波的相位常数便是整个合成波的相位常数.因此,用上面的方法所得的相位常数范围在0~π/L的色散曲线也就是TM01模的基波的色散曲线,沿反方向传播的同一模式的色散曲线便是上面这段曲线关于纵轴的一段对称分布曲线,相位常数的范围也就扩展为-π/L~π/L,由(2)式可知,-1次空间谐波的相位常数范围分为关于纵轴对称的2个部分,-2π/L~-π/L和π/L~2π/L.因为各个空间谐波和合成波的频率一致,所以就可以画出TM01模具有周期性的色散特性曲线.0~2π/L范围的色散曲线如图3所示.

图3 周期性慢波结构的色散曲线
[1]张 军,钟辉煌.高功率 O型微波器件的纵向模式选择研究 [J].物理学报,2005,54(1):206-210.
[2]董 炜,董志伟,周海京.一种数值求解慢波结构色散曲线的新方法 [J].信息与电子工程,2006,4(5):331-336.
[3]王文祥.微波工程技术 [M].北京:国防工业出版社,2009:275-278.
[4]BARUCH L,THOMAS M A,ALAN B,et al.Theory of Relativistic Backward-Wave Oscillators with End Rflections[J].IEEE Transaction on Plasma Science,1992,20(3):263-280.
[5]陈昌华,刘国治,宋志敏,等.相对论返波管慢波结构起始端的设计 [J].强激光也粒子束,2005,17(8):1 121-1 125.
[6]葛行军,陈 宇,钱宝良,等.O型同轴慢波器件的纵向模式选择研究 [J].电报科学学报,2008,23(6):1 111-1 118.
(责任编辑 陈炳权)
Method of Rapidly Computing Dispersion Curves in SWS
YANG Kuo1,2,SHI Cheng-cai1
(1.School of Physical Electronics,University of Electronic Science and Technology of China,Chengdu 610054,China;2.Department of Physics and Electronic Engineering,A’Ba Teacher’s College,Wenchuan 623000,Sichuan China)
Distributing character of fields in SWS is analysed.A method which makes use of the Magic code to compute rapidly dispersion in SWS and to depict it’s curves is proposed.Taking a specific construction as an example,the process of using the method is described elaborately.Meanwhile,the theory of the method is analyzed.Combining the theory of electron magnetic and distributing character of fields in SWS,the feasibility of the method is proved.Although there is somewhat error in the result,it is easily and rapidly operated,so there are some realistic values in the design of some microwave electron structures.
SWS;dispersion character;spacial resonance wave;resonance
O436.3;TN816
A
10.3969/j.issn.1007-2985.2012.03.012
1007-2985(2012)03-0047-03
2012-01-20
四川省科技厅重点科技资助项目(2011JYZ031);四川省教育厅科学研究资助项目(10ZC059);阿坝师专科研课题(ASA11-28)
杨 阔(1980-),男,四川安岳人,阿坝师范高等专科学校电子信息工程系讲师,电子科技大学博士研究生,主要从事物理电子学研究.
