H型钢矫直过程残余应力演变机制研究

管奔，臧勇，逄晓男，吕智勇，刘福宁，冯伟

（1.北京科技大学机械工程学院，北京 100083;2.山东省莱芜钢铁股份有限公司型钢厂，山东莱芜 271126）

H型钢矫直过程残余应力演变机制研究

管奔1，臧勇1，逄晓男2，吕智勇2，刘福宁2，冯伟2

（1.北京科技大学机械工程学院，北京 100083;2.山东省莱芜钢铁股份有限公司型钢厂，山东莱芜 271126）

为在矫直过程中对H型钢的残余应力实施有效地主动控制，对H型钢矫直过程中残余应力演变过程的力学机制进行研究。首先运用弹塑性基本理论对具有初始残余应力的H型钢截面弹塑性反弯过程进行解析分析，论证初始残余应力对截面弹塑性反弯过程的影响方式，证明初始残余应力导致截面弯曲中性轴位移的非对称弯曲状态。在此基础上，利用差分方法建立H型钢矫直过程多次连续弹塑性反弯的数值解法，进而详细研究H型钢矫直过程中残余应力的演变机制。结果表明:截面翼缘与腹板整体拉压应力水平的消减主要依赖矫直前期的非对称弹塑性弯曲过程，而矫直后期的对称弯曲过程则进一步改善H型钢翼缘的残余应力状态;矫直过程前期与后期不同的弹塑性弯曲性质造成了其在矫直过程中对于残余应力演变的不同影响作用。

H型钢;矫直;弹塑性弯曲;应力分布

H型钢作为一种经济断面高效型材，被广泛地应用于制造海洋石油平台等油气开发重型装备中［1－2］。由于此类结构物复杂的使用环境及载荷条件，使其对于H型钢的几何与力学品质有了更加苛刻的要求［3－4］。而多辊矫直过程作为热轧H型钢生产过程中的一道关键的精整工序，很大程度上决定着产品的最终精度和品质［5］。传统矫直过程的主要目的在于对H型钢几何缺陷的矫正，在苛刻的使用环境下则要求在矫直过程中对其残余应力等进行控制。基于梁的弯曲理论［6－9］能够对矫直过程中金属条材几何缺陷的演变进行分析，但并不支持对残余应力演变方式的解析。对残余应力演变过程的研究多是基于有限元方法［5，10－15］，笔者以H型钢矫直过程中的残余应力演变机制为研究对象，提出H型钢残余应力演变方式的数学模型，继而对残余应力的演变规律进行合理分析。

1 H型钢矫前初始残余应力表征

H型钢矫前残余应力分布方式是进行矫直过程残余应力研究的基础。残余应力的内部成因主要包括由温差导致的热应力和因相变导致的相变应力。文献［16］对700×300规格的H型钢残余应力分布方式进行了系统的仿真分析和测试研究，其仿真结果如图1所示。

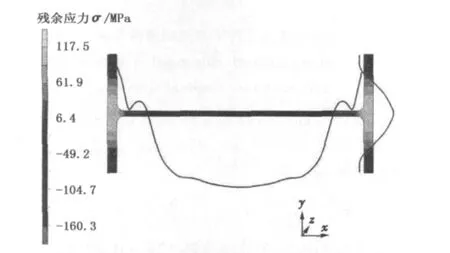
图1 H型钢截面矫前残余应力分布情况Fig.1 Distribu tion of residual stress in H section before straightening

由仿真分析及现场测试结果可知，H型钢矫前腹板部分存在较为均匀分布的残余压应力，而翼缘部分存在沿厚度方向较为均匀、但沿高度方向分布状态有所差异的拉应力。为方便对矫直过程数学模型的计算，对700×300规格H型钢残余应力形式进行合理的简化后，可对其用图2所示的线性模型进行数学表征。

在此模型中，H型钢翼缘总体残余应力分布为双线性函数，由边部残余应力值σc1及中部残余应力值σc2确定。根据测试结果，可定义3类翼缘初始残余应力的分布形式，根据其特征参数，分别命名为（100，100）型、（0，120）型及（－25，150）型。腹板残余应力σc3为均匀分布状态，其数值根据截面残余应力的自平衡性由翼缘残余应力分布函数σcy在翼缘面积AY上的积分与腹板残余应力σc3在腹板面积AF上的积分相等而求得:

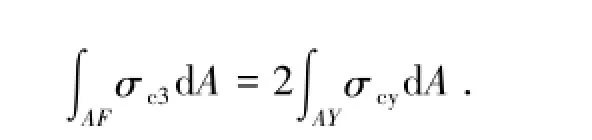
H型钢各型残余应力数值模型的特征值见表1。以后的讨论将基于表1中3类H型钢初始残余应力分布形式展开。

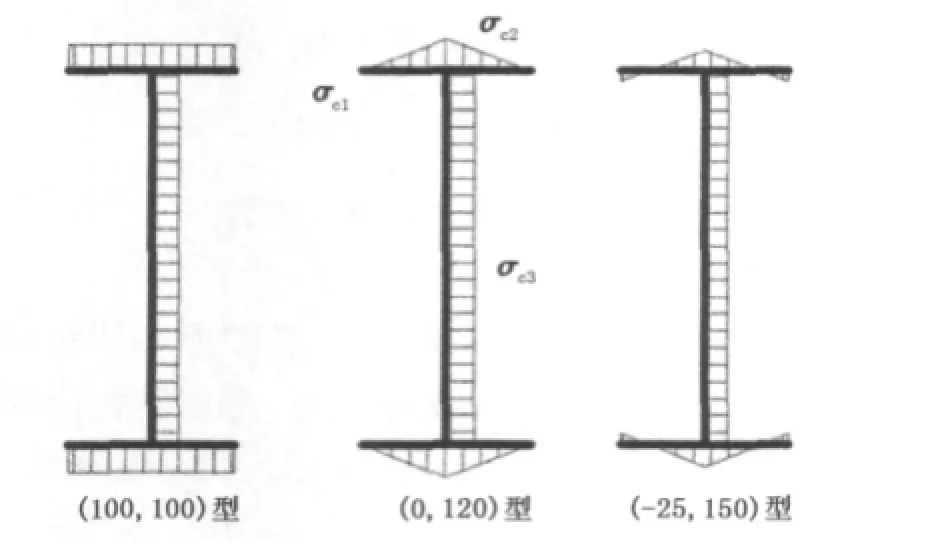
图2 H型钢初始残余应力数学表征Fig.2 M athematical characterization of initial residual stresses of H section

表1 H型钢初始残余应力特征值Tab le 1 Characteristic value of initial residual stresses of H section

2 具有初始残余应力H型钢的矫直弯曲理论分析

2.1 残余应力条件下的截面弹塑性弯曲

H型钢矫直的力学过程即为截面逐次的弹塑性反弯过程，该弹塑性弯曲过程通常适用平截面假设，应变在横截面上线性分布。

2.1.1 无初始应力条件下的截面弹塑性弯曲

当H型钢截面无初始残余应力时，设截面屈服极限为σs，截面弹塑性弯曲状态用弯曲曲率α与截面弹性极限弯曲曲率αt之比C=α/αt表示，H形截面参数及弯曲应力分布如图3所示。

翼缘应力分布函数σY为

为防止断面的畸变，矫直过程截面弹塑性反弯的塑性区一般不会深入达到腹板位置，因此腹板应力分布函数σf为

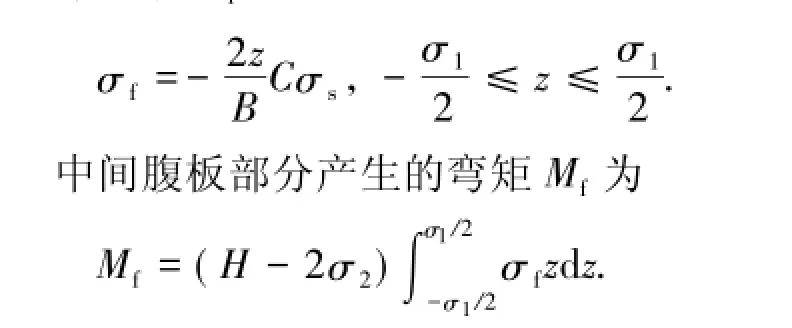
因此，H型截面产生的整体弯矩M为

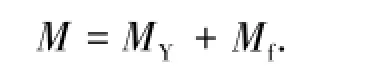
对于H形截面的回弹过程，其截面整体相当于施加一个－M的纯弹性效应弯矩，考虑到截面回弹过程的整体性，截面整体弯曲卸载应力分布函数为

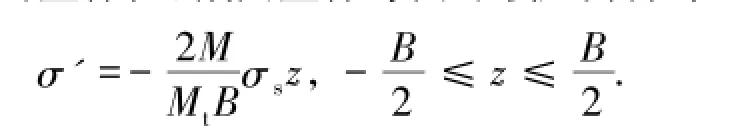
式中，Mt为H形截面的弹性极限弯矩。

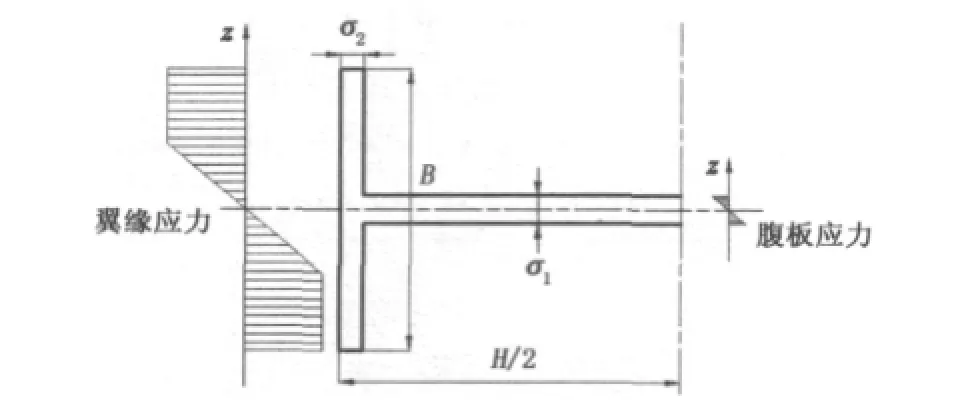
图3 H型钢截面参数与弹塑性弯曲加载应力Fig.3 Section parameters of H beam and loading stress du ring elastic-p lastic bending p rocess

2.1.2 初始应力对截面弹塑性弯曲的影响

在H型截面存在纵向残余应力的条件下，若截面整体弯曲应力都处在弹性状态，则可根据应力的线性叠加效应分析，初始残余应力能够沿纵向保持平衡，截面弯曲造成的叠加应力合力矩与外载弯矩M依然能够保持平衡，截面弯曲中性层保持不变。

然而，当截面进入弹塑性弯曲状态后，截面弯曲过程中应力增量的分布相对于几何中轴对称的性质将不再适用。当截面弯曲增大至一定程度后，反对称的外加弯曲应力和对称的初始应力的叠加，使得截面几何中轴两侧的某一侧率先进入塑性变形，且其应力也不再随着弯曲曲率的增大而增加，而另一侧则不然，从而打破了弯曲造成的应力增量沿截面几何中轴的反对称的分布状态，若弯曲中性轴依然保持与几何中轴重合则不能保证截面纵向应力仍保持平衡的条件，因此存在残余应力的截面进入弹塑性弯曲状态后其中性轴将相对于几何中轴发生位移。

由于截面初始残余应力的状态各有不同，矫直过程中应力分布的解析函数也是不同的。以残余应力分布形式较简单的（100，100）型截面分布形式为例，对其初始应力影响下的弹塑性弯曲过程进行分析（图4）。

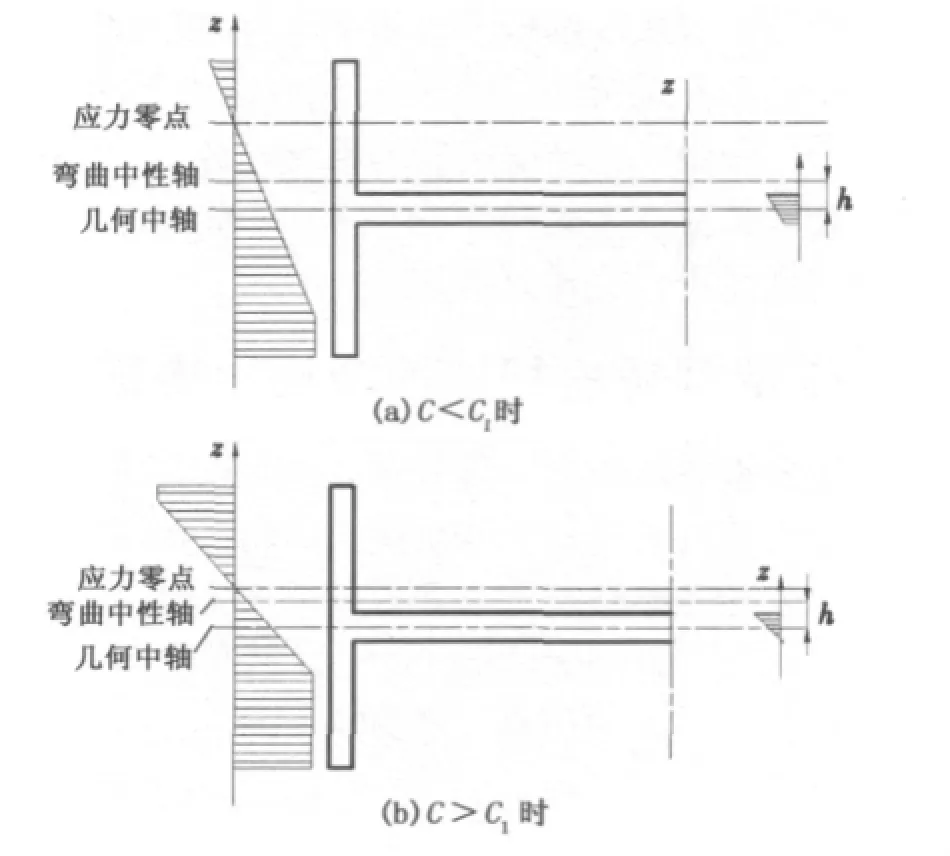
图4 存在残余应力条件下截面弹塑性弯曲加载应力Fig.4 Loading stress during elastic-plastic bending p rocess under residual stresses

设在弹塑性弯曲曲率C的条件下弯曲中性轴相对几何中轴的位移量为h，则弯曲过程叠加的应力增量的函数σ'w为

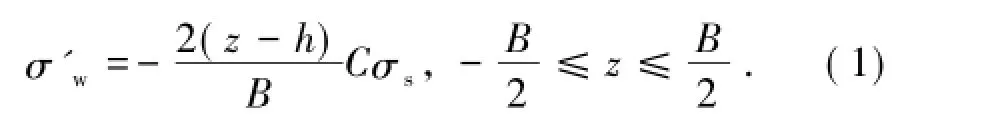
在弹性极限弯曲曲率状态下h=0，则存在初始残余应力条件下的弹性极限弯曲曲率Ct满足

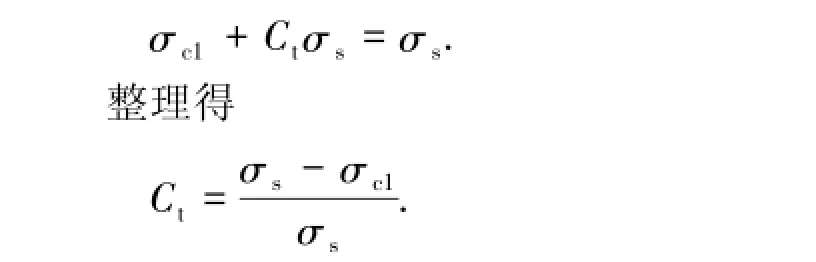
当C＞Ct时，截面翼缘下部首先进入塑性变形状态，其弹塑性分界点z1满足

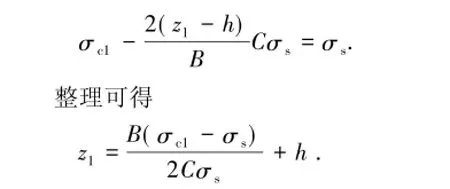
对于两侧翼缘是否都存在塑性状态则需进行判定。若上部翼缘存在区域进入塑性状态，则上部翼缘最外侧满足

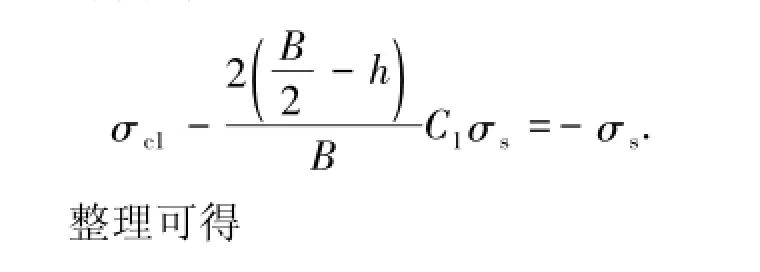
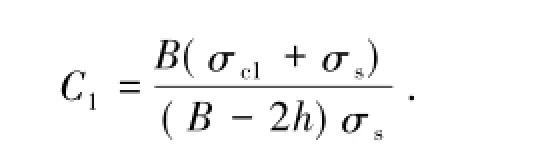
因此，断面应力分布分为两种情况:

①若Ct＜C＜C1，则上部翼缘没有进入塑性状态（图4（a）），可得翼缘应力分布函数σY为

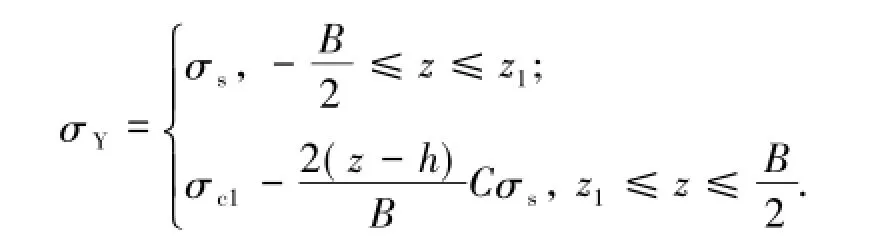
②若C＞C1，则两侧翼缘皆发生塑性变形（图4（b）），上部翼缘弹塑性分界点z2满足

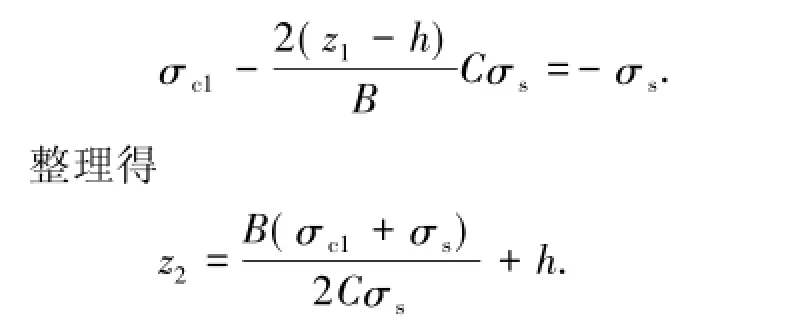
此时翼缘应力分布函数σY为

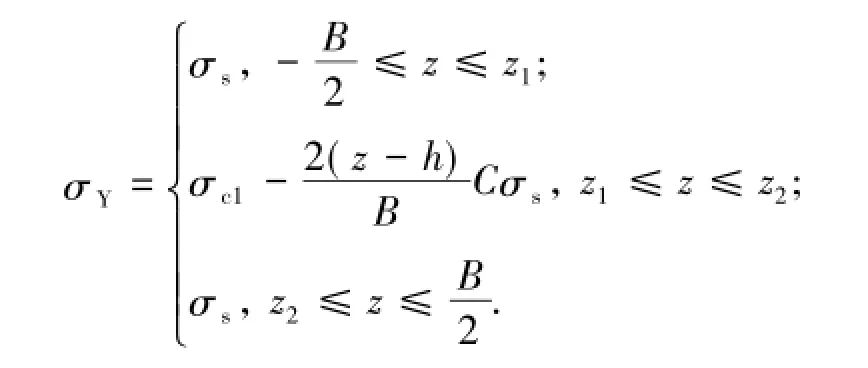
由于腹板一般不会发生塑性变形，同时又存在较高的初始压应力状态，因此认定在弹塑性弯曲过程中腹板不进入塑性变形状态，则腹板应力分布函数σf为

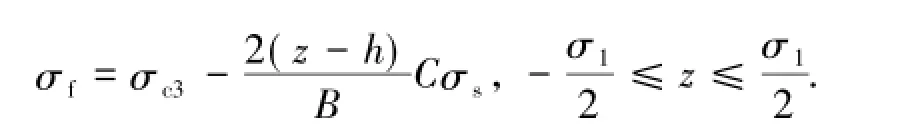
为求得h，需引入截面整体纵向应力平衡条件，即h须使σY及σf满足

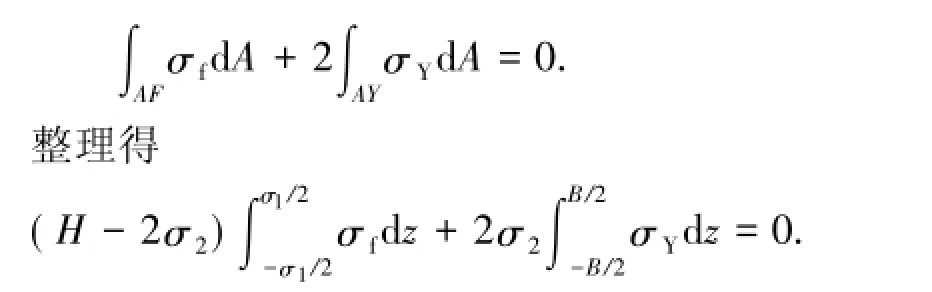
由上式则可求得h，以上各公式得解。对于存在残余应力的截面回弹过程则依然须遵循纯弹性回弹的原则，即回弹应力以几何中轴为中性轴，以总体弯矩M进行回弹，以此原则回弹可满足截面回弹后纵向应力及静矩的平衡条件，回弹应力分布函数计算思路与无初始残余应力条件一致。

2.2 矫直过程连续弯曲的数值求解

通过对存在初始残余应力的H型截面弯曲过程的力学解析可以发现，其弯曲过程的数学关系还是较为复杂的，若叠加更为复杂的初始残余应力分布函数，则不易获得具体解析公式，而对于求解截面矫直过程的多次弹塑性反弯更难以得到解析解。因此，采用对截面应力分布进行有限差分的数值方法求解矫直过程，该数值方法的具体思路在文献［17］中已经有了较为详细的阐述，而将该算法用于计算具有初始残余应力的H型钢截面弯曲过程则需要在计算流程中附加搜索判定条件。

设定弯曲曲率C后，应当求得初始残余应力影响下的截面中性轴位移量h，从而获得截面应力分布函数。具体方法是:首先给出中性轴位移量h的搜索范围［x1，x2］与合力误差范围ε1，然后给定某一中性轴初始位移量h0，则由式（1）与屈服判定准则可得差分化的翼缘加载应力函数σYΔ与腹板加载应力函数σfΔ。对σYΔ与σfΔ进行数值积分，判定其是否满足以下条件:

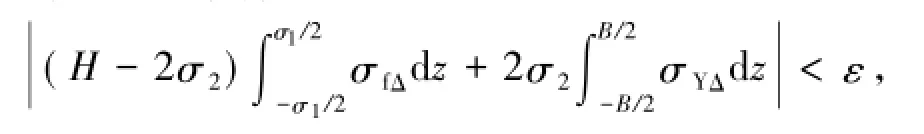
若不满足，则根据不同数值搜索方法继续赋值h，循环以上步骤达到条件满足并输出截面翼缘与腹板的应力分布函数。

3 残余应力演变分析

利用以上数值求解模型，对700×300规格H型钢6辊4次弯曲矫直过程中的应力演变进行分析，H型钢的屈服极限σs=235 MPa。矫直过程中型钢的初始曲率及压弯曲率皆由实际曲率与截面弹性极限弯曲曲率αt之比的方式给出，即初始曲率比C0= α0/αt，弯曲曲率比Cw=αw/αt，其中α0为实际初始曲率，αw为实际弯曲曲率。H型钢的最大初始曲率比设为C0max=±1，各截面初始曲率在该条材上随机连续分布，矫直过程的四次弯曲中的弯曲曲率比Cw分别为3，－2，1.5及－1.11。对于矫直过程的数值求解参数采用对H型钢截面翼缘自－1500至+1500等分为3001个区段点，对腹板自－65至+65等分为130个区段点，极小误差范围取ε＜0.001，对于中性轴位移量h的搜索采用翼缘高度［－150，150］范围内的二分法。

3.1 矫后残余应力分布

各种初始残余应力条件下H型钢不同初始曲率截面的翼缘矫后残余应力分布状态如图5所示。可以看出，H型钢不同初始曲率截面经过矫直以后翼缘残余应力分布方式基本相同，其中翼缘边部残余应力分布及数值极为一致，而中部残余应力分布形式略有不同。对比矫前初始残余应力状态可以看出，矫后各截面翼缘边部的残余应力数值有所下降，而翼缘中部的残余应力数值上升，而且无论矫前初始应力分布形式如何，经历矫后截面残余应力分布形式都是基本相同的。H型钢腹板由于一直未进入塑性变形状态，因而其残余应力一直处于线性变化的过程中。

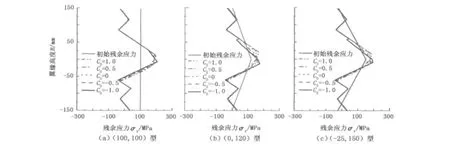
图5 H型钢不同初始曲率截面矫后翼缘残余应力分布Fig.5 Distribu tion of residual stress on flange of H section w ith d ifferent initial curvatu re

3.2 矫直过程中截面残余应力参数的演变

H型钢截面残余应力状态对其承载能力的影响主要由H型钢翼缘部分的总体残余应力绝对值的水平决定［18］，同时，H型钢初始残余应力形成的基础为冷却温差所导致的翼缘整体拉应力状态及腹板整体的压应力状态，因此H型钢翼缘的整体残余拉应力水平及腹板的整体残余压应力水平是影响H型钢矫后定尺切割等后续加工过程中构件再次发生局部或整体变形的主要因素。

综合考虑矫后H型钢截面残余应力在其承载能力及后续加工过程中的不同影响方式，定义翼缘纵向平均应力σYz与腹板纵向平均应力σfz两参数分析H型钢截面矫直过程中翼缘与腹板的整体拉压应力水平，定义翼缘纵向应力绝对值平均值σYc¯a代表截面翼缘部分的总体残余应力水平。各参数的定义与数值计算方法如下:

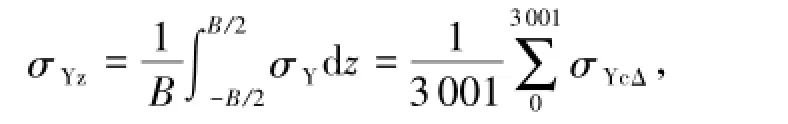
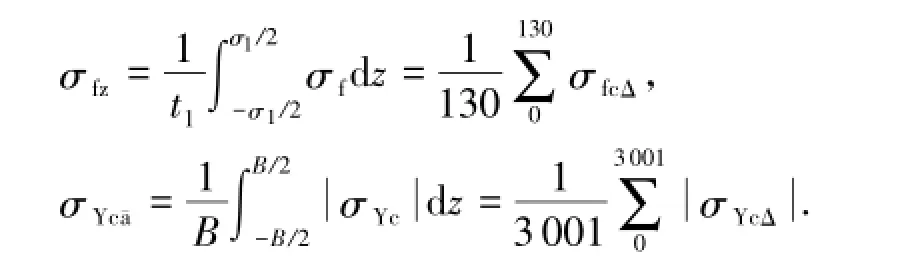
H型钢的各不同初始曲率截面的各残余应力演变参数的计算结果如图6～8所示。可见，对于σYc¯a代表的翼缘部分总体残余应力:（100，100）型条材残余应力水平在经历各次弯曲后都有所下降，条材中具有正向初始曲率截面的残余应力水平略高; （0，120）型及（－25，150）型残余应力在第1次弯曲后截面残余应力水平上升，在其后的弯曲过程中残余应力水平逐渐下降，在经历第4次弯曲后各截面残余应力水平开始低于初始残余应力水平，具有正向初始曲率截面的残余应力水平略高。代表翼缘与腹板整体拉压状态的两参数σYz与σfz，在条材经历第1、2次弯曲过程之中有较大的下降趋势，而在矫直后期的第3、4次弯曲过程则不再发生变化。

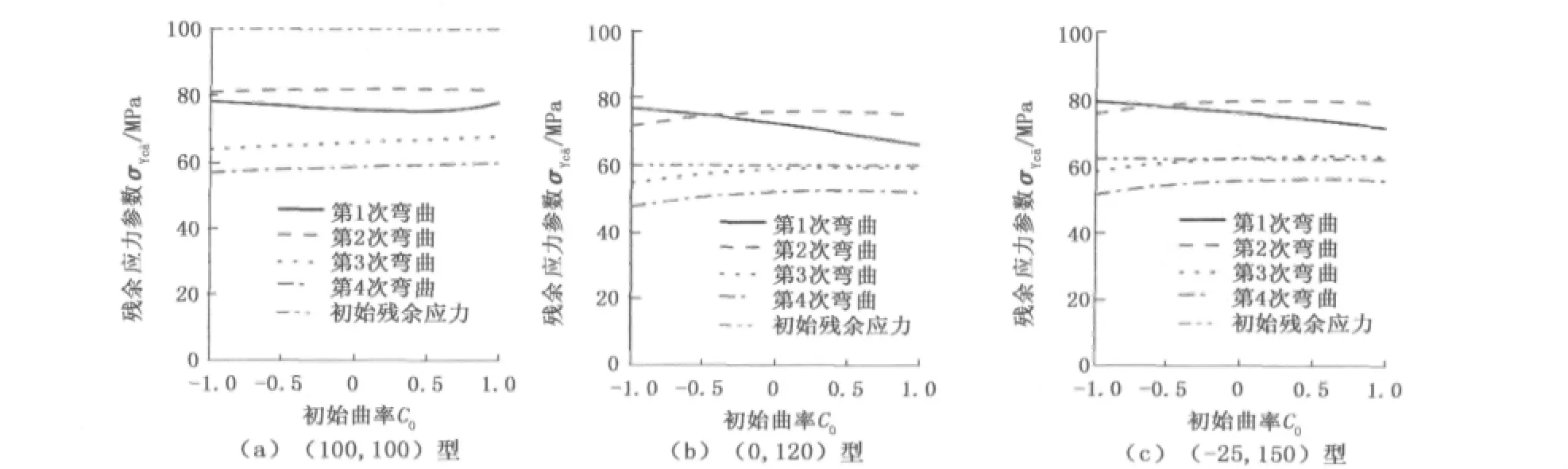
图6 H型钢条材σYc¯a参数演变过程Fig.6 Evolu tion p rocess of param eterσYc¯a of H beam

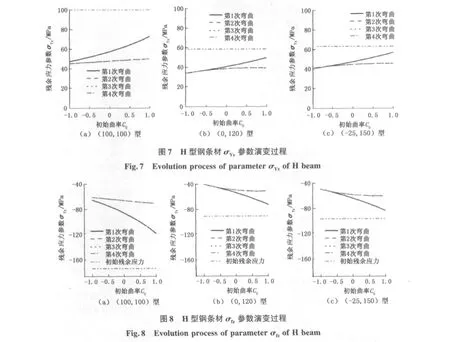
参数σfz及σYz的演变过程与矫直过程中截面弹塑性弯曲中性轴的位移量h的演变是一致的。以（100，100）型H型钢C0max=－1截面矫直过程中截面中性轴位移量h与σfz及σYz的关系为例，分析其演变规律，结果见图9。可以看出，由于H型钢截面初始残余应力的影响，造成矫直前期弯曲过程的中性轴存在位移量h，同时两残余应力参数在矫直过程中的数值也随之下降，但是随着前期弯曲过程使截面翼缘两侧边部残余应力的趋于一致及矫直后期弯曲塑性区的减小，弹塑性弯曲过程的中性轴不再存在位移或仅产生很小位移，截面完全处在沿几何对称轴弯曲的状态，σfz及σYz也将不会再有所减小。同时还可以看出，该截面另一残余应力参数σYc¯a不存在这种与弯曲中性轴位移量h一致的演变关系，而是随着矫直过程的不断进行而保持持续下降的趋势。

由此可见，矫直过程对于改善H型钢矫后后续加工中由于截面残余应力引发的再次变形等问题，实际上是矫直前期的非对称弹塑性反弯起主要作用，而后期截面对称弹塑性反弯的意义则在于进一步减小翼缘残余应力分布的绝对数值从而改善其使用过程中的承载能力。这也与生产实践中对于所谓“残余应力释放”主要来自于矫直前次弯曲过程的直观认识是一致的。

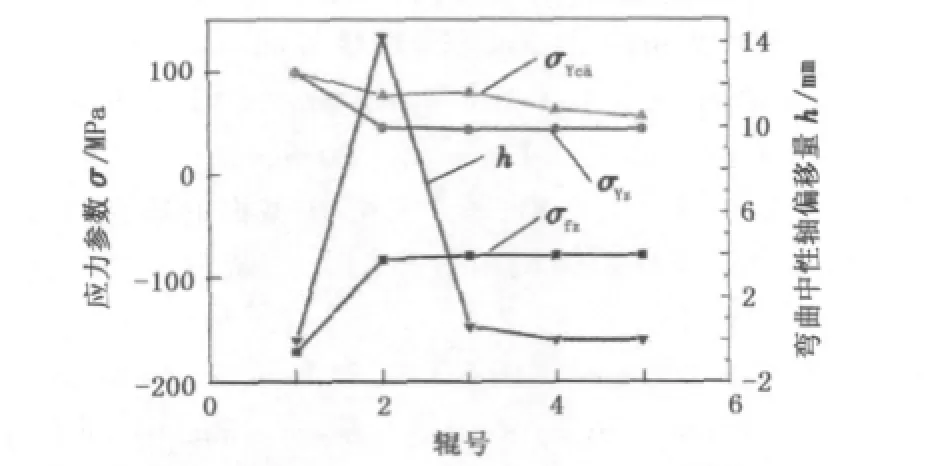
图9 典型截面各参数在矫直过程中的演变规律Fig.9 Evolu tion law of parameters of typ ical section during straigh tening p rocess

4 结论

（1）由于H型钢截面初始应力的影响，其矫直过程中的弹塑性反弯过程实际上是相对于截面几何中轴非对称的弯曲过程，该弯曲过程可以通过离散截面的有限差分方法进行数值运算。

（2）矫前任何初始应力状态的H型钢，其矫后翼缘残余应力分布形式趋于一致;从截面分布上看，翼缘边部的残余应力数值有所减小而中部的残余应力数值则有所增大。

（3）截面翼缘与腹板整体拉压应力水平的消减主要由矫直前期的非对称弯曲过程发挥作用，继而改善了构件后续的加工条件;矫直后期的对称弯曲过程进一步优化了截面翼缘的残余应力状态，继而改善了其使用过程中的承载能力。

［1］孙维，汪开忠.海洋石油平台用热轧H型钢生产工艺的优化［J］.中国冶金，2004（5）:15－21.

SUNWei，WANG Kai－zhong.Optimization of productive technology of H－beam used for offshore oil platform［J］. China Metallurgy，2004（5）:15－21.

［2］顾建国.海洋石油平台用H型钢的开发研究［J］.钢铁，2001，36（2）:29－33.

GU Jian－guo.Developmentand research of H－beam using for offshore oil drilling platform［J］.Iron and Steel，2001，36（2）:29－33.

［3］陈团海，陈国明，许亮斌.基于台风验证载荷的平台时变可靠性分析与更新［J］.中国石油大学学报:自然科学版，2011，35（3）:129－134，139.

CHEN Tuan－hai，CHEN Guo－ming，XU Liang－bin. Time－dependent reliability analysis and updating of offshore platforms based on typhoon proof load［J］.Journal of China University of Petroleum（Edition of Natural Science），2011，35（3）:129－134，139.

［4］杨秀娟，修宗祥，闫相祯，等.基于疲劳可靠性优化设计的深水导管架平台多级模糊选型［J］.中国石油大学学报:自然科学版，2010，34（2）:98－103.

YANG Xiu－juan，XIU Zong－xiang，YAN Xiang－zhen，et al.Fuzzy lectotype of deep water jacket platform based on fatigue reliability optimization design［J］.Journal of China University of Petroleum（Edition of Natural Science），2010，34（2）:98－103.

［5］崔丽红，臧勇，章博，等.多辊矫直过程中H型钢断面的应力演变规律［J］.北京科技大学学报，2008，30 （8）:942－946.

CUI Li－hong，ZANG Yong，ZHANG Bo，et al.Stress evolvement rule of an H－beam section during multi－roller straightening process［J］.J Univ Sci Technol Beijing，2008，30（8）:942－946.

［6］崔甫.矫直理论与参数计算［M］.北京:机械工业出版社，1987.

［7］臧勇，王会刚，崔福龙.型钢辊式矫直压弯挠度的弹塑性解析［J］.机械工程学报，2005，41（11）:47－52.

ZANG Yong，WANG Hui－gang，CUI Fu－long.Elasticplasticity analyses of bending deflection on section roller straightening［J］.Chinese Journal of Mechanical Engineering，2005，41（11）:47－52.

［8］王会刚.H型钢矫直机制及有限元动态仿真研究［D］.北京:北京科技大学机械工程学院，2005.

WANG Hui－gang.Study on H－beam straighteningmechanism and dynam ic FEM simulation［D］.Beijing:School of Mechanical Engineering，University of Science and Technology Beijing，2005.

［9］周存龙，王国栋，谢东钢，等.辊式矫直过程中板带弯曲挠度的确定［J］.太原科技大学学报，2009，30（1）: 48－50.

ZHOU Cun－long，WANG Guo－dong，XIE Dong－gang，et al.Effect of entrance/exit leveler roller intermesh to plate flatness［J］.Journal of Taiyuan University of Science and Technology，2009，30（1）:48－50.

［10］SCHLEINZER G，FISCHER F D.Residual stress formation during the roller straightening of railway rails［J］.International Journal of Mechanical Sciences，2001，43（10）:2281－2295.

［11］杨文庆，陈林，赵玉萍，等.重轨矫直变形过程的有限元模拟计算分析［J］.包头钢铁学院学报，2005，24 （3）:284－287.

YANGWen－qing，CHEN Lin，ZHAO Yu－ping，et al. Finite element simulation and calculation analysis on the straightening and deformation of heavy rail finite element［J］.Journal of Baotou University of Iron and Steel Technology，2005，24（3）:284－287.

［12］周文，刘学毅.高速道岔尖轨矫直的有限元分析［J］.西南交通大学学报，2008，43（1）:82－85.

ZHOUWen，LIU Xue－yi.FEM simulation of straightening tongue rail of high－speed turnout［J］.Journal of Southwest Jiaotong University，2008，43（1）:82－85.

［13］王建国，陈林，李浩，等.大型H型钢的矫直过程应力分布规律数值模拟分析［J］.冶金设备，2012（增刊）:17－18.

WANG Jian－guo，CHEN Lin，LIHao，et al.Numerical simulation analysis of large H－beam straightening［J］. Metallurgical Equipment，2012（sup）:17－18.

［14］黄华栋，臧勇.H型钢矫直过程的有限元仿真［J］.制造技术与机床，2012（5）:110－115.

HUANG Hua－dong，ZANG Yong.The FEM simulation of H－beam straightening［J］.Manufacturing Technology＆Machine Tool，2012（5）:110－115.

［15］周剑华，吉玉，吴迪.辊式水平矫直60kg/m重轨断面应力应变分析［J］.塑性工程学报，2011，18（3）:39－42.

ZHOU Jian－hua，JIYu，WU Di.Analysis of the stress and strain on the section of 60kg/m heavy rail in the process of level roller straightening［J］.Journalof Plasticity Engineering，2011，18（3）:39－42.

［16］ZANG Yong，ZHANGBo，CUILi－hong.The analysis of temperature field and residual stress distribution during H－beam cooling process［J］.Advanced Materials Research，2011，194/196:20.

［17］管奔，臧勇，曲为壮，等.辊式矫直过程应力演变及其对反弯特性的影响［J］.机械工程学报，2012，48 （2）:81－86.

GUAN Ben，ZANG Yong，QU Wei－zhuang，et al. Stress evolvement and its influence on bending behavior during roller leveling process［J］.Chinese Journal of Mechanical Engineering，2012，48（2）:81－86.

［18］王轶平.薄壁H形截面轴心受压构件承载能力及其缺陷敏感性研究［D］.北京:北京科技大学机械工程学院，2010.

WANG Yi－ping.Study on carrying capacity and imperfection sensitivity of H section columns［D］.Beijing: School ofMechanical Engineering，University of Science and Technology Beijing，2010.

Study on residual stresses evolution m echanism of H-beam during straightening process

GUAN Ben1，ZANG Yong1，PANG Xiao－nan2，LÜZhi－yong2，LIU Fu－ning2，FENGWei2
（1.School of Mechanical Engineering，University of Science and Technology Beijing，Beijing 100083，China; 2.Section Mill of Laiwu Iron＆Steel Company Limited，Laiwu 271126，China）

In order to control the residual stress of H－beam during the straightening process effectively，themechanicalmechanism behind the evolution of residual stresswas studied during the straightening process.The elastic－p lastic bending process of H－beam section with initial residual stress was considered analytically based on the elastoplastic bending theory.The way that the initial residual stress affects the elastic－plastic bending processwas demonstrated，and it is also proved that initial residual stress of the section leads to the asymmetric bending of the displacementof the section neutral axis.On thebasisof the analysis，a differencemethod was established to describe the continuous bending process of H－beam during the straightening process.The evolution mechanisms of H－beam residual stress during the straightening processwas studied.The results show that the asymmetric elastic－plastic bending process at the earlier stage of straightening process is themain reason for reducing the tension－compression stress state of the web and flange，while the symmetrical bending process in later stageof the straightening process further improves the residual stress state of the flange.The different elastoplastic bending properties during the early and later stage of the straightening process play different roles in the evolution of residual stresses during the straightening process.

H－beam;straightening;elastic－plastic bending;stress distribution

TG 333.2

A

10.3969/j.issn.1673－5005.2012.05.023

1673－5005（2012）05－0122－07

2012－07－05

国家“863”高技术研究发展计划项目（2009AA03Z515）;国家自然科学基金项目（50775010）

管奔（1985－），男（汉族），山东单县人，博士研究生，主要研究方向为塑性加工工艺及装备。

（编辑 沈玉英）