低渗透应力敏感气藏压裂井产能分析

张 强，王永清，张 楠，杨玲智，蒋 睿

(油气藏地质及开发工程国家重点实验室西南石油大学，四川 成都 610500)

低渗透应力敏感气藏压裂井产能分析

张 强，王永清，张 楠，杨玲智，蒋 睿

(油气藏地质及开发工程国家重点实验室西南石油大学，四川 成都 610500)

应用保角变换原理，将平面垂直裂缝气井的渗流问题转化为易于求解的一维带状渗流问题。基于Forchheimer二项式渗流方程，考虑启动压力梯度和渗透率应力敏感性的影响，推导得到低渗透应力敏感气藏中垂直裂缝井的产能公式，并简化得到低压、高压条件下的产量公式。用现场数据对公式进行验证，并绘制分析了理论产能曲线。结果表明:启动压力梯度和应力敏感性会影响压裂井的产能，压裂气井的产量随着启动压力梯度或者应力敏感性的增加而降低;当气井高产时，必须考虑非达西渗流效应。

启动压力梯度;应力敏感;压裂井;产能;低渗透气藏

引言

低渗透气藏中，由于地层渗透率的应力敏感性和启动压力梯度的存在，使得多数井自然产能较低，必须实施压裂改造措施才具备生产能力。为指导现场生产，近年来有关气藏垂直裂缝井的产能研究较多［1－6］，基本采用双线性流模型、保角变换法、椭圆流动法以及数值模拟等方法，但考虑气体非线性渗流、启动压力梯度以及应力敏感因素的研究不多，因此现场应用时具有一定的局限性。为此，笔者从Forchheimer非达西渗流理论出发，应用保角变换方法推导出一种相对简单的、考虑启动压力梯度的低渗透应力敏感气藏无限导流垂直裂缝井产能方程。

1 模型的建立及讨论

1.1 地质模型的假设

假设:均质等厚圆形应力敏感气藏中心一口压裂井等温稳定生产;无限导流裂缝呈矩形、垂直、对称分布于气井两边，忽略裂缝宽度，裂缝半长为Lf;产层全部打开，厚度为h;地层泄油半径为Re，其压力为pe，井底压力为pwf;地层均质且各向同性;忽略重力和毛管力;气体流动符合Forchheimer非达西渗流且考虑启动压力梯度。

1.2 产量公式的建立

利用保角变换［7－8］可将平面上围绕裂缝面的椭圆流动转换为宽度为π的一维带状流动。结合Forchheimer非达西渗流定律，可得考虑启动压力梯度的一维渗流方程:

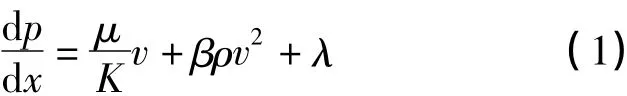
式中:p为地层压力，MPa;x为距离井底位置，m;μ为气体黏度，mPa·s;K为地层渗透率，10－3μm2;β为紊流系数，m－1;ρ为天然气密度，kg/m3;v为气体渗流速度，m/s;λ为启动压力梯度，MPa/m。

气体和介质渗透率的状态方程为:

式中:Z为储层温度下的气体压缩因子;T为储层温度，K;Ck为渗透率模数，1/MPa;下标i为原始状态下的相关参数;下标sc为标准状况下的相关参数;a=7.644×1010。

式中:φe和φwf分别为气藏外边界和井底的拟压力，MPa·m3/d;qsc为气井压裂后地面产量，m3/d;h为气层有效厚度，m;pe为气藏外边界压力，MPa;pwf为井底流压，MPa;M为天然气分子质量;R为气体常数，0.008 314 MPa·m3·kmol－1·K－1;L为供给边界到井底的距离，m;为天然气平均黏度，mPa·s;为气藏平均渗透率，10－3μm2。

对式(3)右边第三项进行简化:

由此，可得考虑启动压力梯度和应力敏感的压裂气井产量公式:

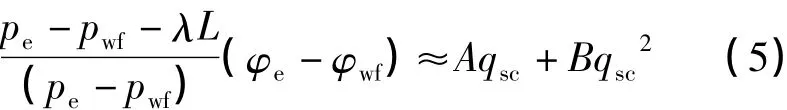
式中:Lf为裂缝半长，m;Re为气藏供给边界，m;γg为天然气相对密度。

1.3 公式的讨论

当地层压力低于12 MPa［9－10］、μZ=常数时，式(5)简化如下:

当地层为非敏感地层，即Ck→0时，可将式(6)简化为:

当不存在启动压力梯度时，即λ=0时，产量公式(7)简化为:

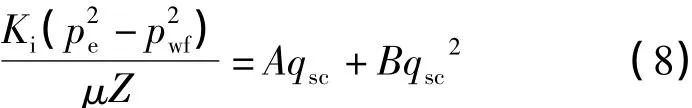
当地层压力高于21 MPa［9－10］、p/μZ=b(b为常数)，产量公式(5)简化如下:

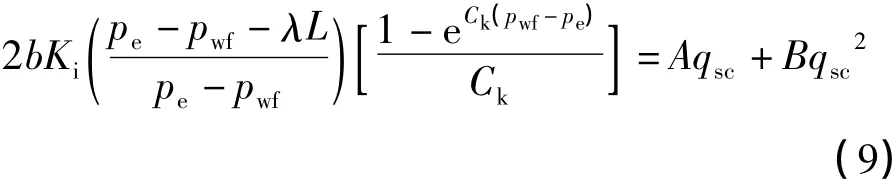
当不考虑应力敏感因素，即Ck→0时，式(9)可简化为:

当不存在启动压力梯度时，式(10)可再简化为:

2 公式的验证以及产能曲线分析

图1 渗透率模数对压裂气井产量的影响

应用文献［2］中的数据来验证产量公式。主要油藏数据如下:气藏边界压力为8.6 MPa，井底流压为6.5 MPa，气藏温度为83℃，基质渗透率为0.75×10－3μm2，气藏有效厚度为11.4 m，地下气体黏度为0.018 5 mPa·s，裂缝半长为400 m，气体压缩因子为0.7，气体相对密度为0.58，压裂后的稳定产量约为40 000 m3/d。由此参数利用式(5)可得压裂井产量为 41 576 m3/d，相对误差为3.94%。因此，本文公式满足油藏工程的计算需要，且计算精度可靠。

介质渗透率模数、启动压力梯度以及非达西渗流效应对气井产量的影响见图1～3。从图中可知:介质变形的渗透率模数、启动压力梯度以及气体紊流均对产能存在不同程度的影响，并且渗透率模数越大、渗流速度越大、启动压力梯度越大，气井的产能越小;图1中，随着应力敏感性的增加，其无阻流量分别比不考虑应力敏感时的低2.68%， 7.73%，12.4%。对于高产气井，非达西渗流效应不能忽略，考虑紊流项比忽略紊流项时的无阻流量低4.75%。因此，对压裂气井进行配产时，必须考虑启动压力梯度以及介质变形和渗流速度的影响。对高产气井，须考虑紊流效应。

图2 启动压力梯度对压裂气井产量的影响

图3 非达西效应对压裂气井产量的影响

3 结论

(1)所推导的产量公式(5)综合考虑了启动压力梯度、应力敏感以及垂直裂缝的影响，且形式简单，精度可靠。还分别讨论了其在高压、低压情况下的产量公式。

(2)基于所得的公式，绘制了无限导流垂直裂缝井的IPR曲线。对其分析可知:在其他条件相同的情况下，启动压力梯度、渗透率模数均对产能存在不同程度的影响，并且启动压力梯度越大，渗透率模数越大，气井的产能越小。因此，在对低渗透气藏压裂井合理配产时，必须考虑启动压力梯度以及介质变形的影响。对高产气井，必须考虑非达西流效应。

［1］蒋廷学，汪绪刚，刘继霞.压裂气井稳态产能研究［J］.天然气工业，2003，23(2):82－84.

［2］汪永利，蒋廷学，曾斌.气井压后稳态产能的计算［J］.石油学报，2003，24(4):65－68.

［3］郭晶晶，张烈辉，梁斌.考虑启动压力梯度的低渗透气藏压裂井产能分析［J］.天然气工业，2010，30(7):45－47.

［4］罗天雨，赵金洲，郭建春.求取压裂后气井产能的椭圆流方法［J］.天然气工业2005，25(10):94－96.

［5］何应付，徐联玉，吕万一，等.低渗透气藏压裂井产能分析［J］.特种油气藏，2006，13(5):71－73.

［6］杨正明，张松，张训华，等.气井压后稳态产能公式和压裂数值模拟研究［J］.天然气工业，2003，23(4):74－76.

［7］张伟东，杨铁军，蒋廷学，等.保角变换法用于计算压裂井产能［J］.油气地质与采收率，2003，10(增刊):81－82.

［8］张强，王永清，章双龙，等.考虑启动压力和二次梯度的压裂井稳态渗流模型［J］.特种油气藏，2011，18 (6):89－91.

［9］谭羽飞，廉乐明，严铭卿.真实气体拟压力的计算［J］.煤气与热力，2010，19(2):31－33.

［10］马时刚，苏彦春，王世民，等.拟压力不同简化形式对气井产能计算的影响［J］.天然气勘探与开发，2010，33(3):30－32.

Analysis of fractured well productivity in low－permeability stress－sensitive gas reservoir

ZHANG Qiang，WANG Yong－qing，ZHANG Nan，YANG Ling－zhi，JIANG Rui
(State Key Laboratory of Oil＆Gas Reservoir Geology and Exploitation，Southwest Petroleum University，Chengdu，Sichuan610500，China)

The seepage problem in gas well with vertical fractures is converted to one－dimensional ribbon seepage which is easy to be solved by using conformal transformation principle.Based on Forchheimer binomial flow equation，a productivity formula of wells with vertical fractures in low－permeability stress－sensitive gas reservoirs has been deduced by taking account of threshold pressure gradient and stress sensitivity of permeability，and a production formula under conditions of low pressure and high pressure has been derived through simplification.The formulas have been verified with field data，and theoretical production curve has been constructed and analyzed.The results show that threshold pressure gradient and stress sensitivity can influence the productivity of fractured wells;the production of fractured gas wells decreases with the increase of threshold pressure gradient or stress sensitivity;when gas well is high yielding，non－Darcy flow effect must be considered.

threshold pressure gradient;stress sensitivity;fractured well;productivity;low permeability gas reservoir

TE328

A

1006－6535(2012)03－0074－03

10.3969/j.issn.1006－6535.2012.03.018

20110527;改回日期:20120312

国家科技重大专项“大型油气田及煤层气开发”(2008ZX05048)

张强(1985－)，男，2009年毕业于大庆石油学院信息与计算科学专业，现为西南石油大学油气田开发专业在读硕士研究生，主要从事油气田开发方面的研究。

编辑姜 岭