四色够不够

　　上幼儿园甚至更早的时候，大家都玩过填色游戏，我们可以在一幅画好线条的图画里任意填上自己喜欢的颜色；现在，大家上了小学，接触到了地图，会看到地图上每个行政区划都填上了颜色。其实，给地图填色也是一种填色游戏，一百多年前，有个人假设了一个只用四种颜色给地图填色的游戏，这个游戏直到今天还有人孜孜不倦地玩着呢。
　　右边是一幅需要填色的图。大家都知道，这是灰太狼的形象，可是我们填色的时候却不一定非要填上灰色。我们可以把它填成紫太狼、绿太狼、黑太狼，还可以填成五颜六色花太狼，全凭自己高兴。
　　右边是某个国家的地图。这个国家有11个省级行政区划，该怎么填色呢? 　 给地图填色，能不能全凭自己高兴，想填什么颜色就填什么颜色?弄清这个问题之前，我们要先想想，为什么要给地图填色，纯白色的不好吗?显然，把一幅地图的各个小块填上颜色，是为了使各小块之间有所区别，使人们很快就能辨认查找出来。要知道，人们绘制地图是为了实用，而不是为了观赏，所以，方便第一!
　　这样看来，就不能给一幅地图填上单一的颜色了，因为单一的颜色会使地图相邻各区域的边界弱化，不容易辨认出来，从而弱化了地图的实用功能。那是不是应该给地图各区域填上各不相同的颜色呢?我们来看看实际情况吧：中国有34个省级行政区划，就要用34种不同的颜色：世界地图上有200多个国家和地区，就要用上200多种不同的颜色。我们知道，颜色划分越细致，色差越小，当颜色越用越多的时候，仍然会出现边界弱化的问题。
　　如今，人们的解决办法是：使用少数几种比较鲜明的颜色给地图填色，地图上相邻各区域填不同颜色。大家可以找来中国行政区划图看一看，上面一共用了几种颜色?各是哪些颜色?
　　那么，绘制一幅地图只需要用几种颜色，就能把相邻的区域区分开来呢?
　　有两个区域的图，只需要两种颜色(如图1)。
　　
　　有三个区域的图，若这三个区域两两相邻，则需要三种颜色(如图2)。
　　
　　有四个区域的图，若这四个区域是两两相邻，则需要四种颜色(如图3)。
　　
　　有五个区域的图，若有四个区域是两两相邻，则需要四种颜色(如图4)。
　　
　　有六个区域的图，若有四个区域是两两相邻，则需要四种颜色(如图5)。
　　
　　于是，人们猜想，不管什么地图，是不是最多只需要四种颜色就能把各个相邻的区域分开呢?
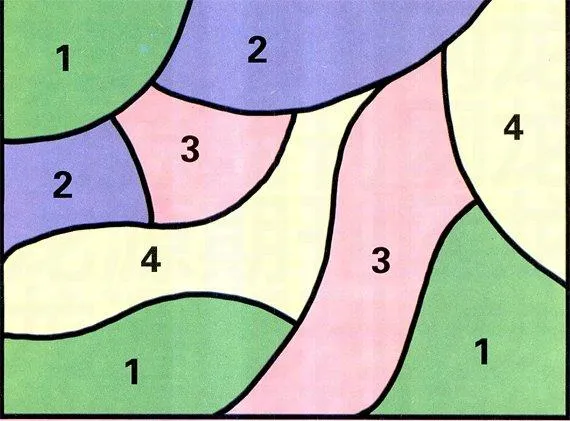
　　最早提出这个猜想的是英国一名大学生，这个猜想引起了数学家们的兴趣，他们不断想办法去证明它，这个猜想就叫四色猜想。它的内容是：任何一幅地图，只用四种颜色就能使具有共同边界的国家着上不同的颜色。换句话说，如果将一个平面任意分为不相重叠的区域，每个区域都可以用1、2、3、4这四个数字之一来标记，并且相邻的两个区域不会得到相同的数字。
　　四色猜想和费马猜想、哥德巴赫猜想一起，被誉为世界近代数学界大三难题。许多科学家为了证明四色猜想，耗费了多年心血。1939年，美国数学家富兰克林证明了22国以下的地图都可以用四色着色。1950年，有人从22国推进到35国。1960年，又有人证明了39国以下的地图可以用四色着色；随后又推进到50国……计算机的问世，大大加快了证明四色猜想的过程。1972年8月，美国两个科学家用两台电脑，耗时1200小时，作了100亿次判断，终于完成了四色猜想的证明，轰动了世界。
　　不过，不少数学家并不满足于计算机所取得的成就，他们认为计算机是由人控制的，证明过程也许会存在设计上或操作上的错误，因此力求寻找一种简单快捷的书面证明方法。直到今天，许多数学家和数学爱好者仍然为此而努力着。与此同时，四色填图作为一种益智游戏，在人群中广泛流行开来。
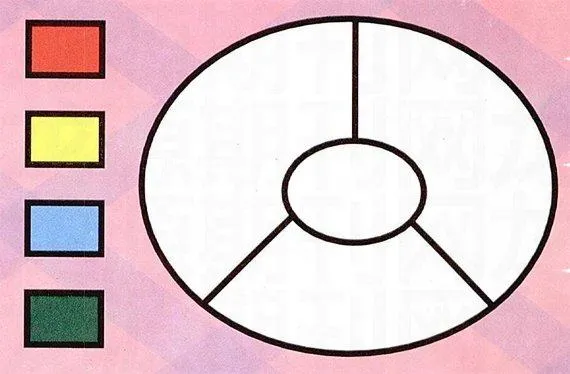
　　第一个小游戏：
　　请用红、黄、蓝、绿这四种颜色给右边这个图形涂色，每个区域涂一种颜色，相邻区域不可同色。请问有多少种涂法?
　　第二个小游戏：
　　下面是一幅中国行政区划空白地图，王友们，快快动手为它着色吧，要求最多可用四种不同的颜色，每种颜色可重复使用，但地图中各相邻区域不能使用同一种颜色