有效追问成就精彩课堂

　　追问，通俗地说就是追根究底地问，它是教师针对某一内容或某一问题，在学生有了一定理解之后的再次补充和深化，是有针对性的“二度提问”，再次激活学生思维，促进他们进行深入探究，自主地构建知识体系。教师适时、有效的追问可以化迷茫为清晰，化粗浅为深入，化平淡为神奇，使课堂锦上添花，促进学生生动活泼地发展。
　　一、学生思维困顿时的追问——柳暗花明
　　在解决问题的过程中，学生的思维有时会遇到障碍或产生矛盾，不能进一步思考、解释、分析。此时，教师应针对学生的思维堵塞积极引导，及时追问，启发学生的思维，开拓他们的思路，促进问题的有效解决。
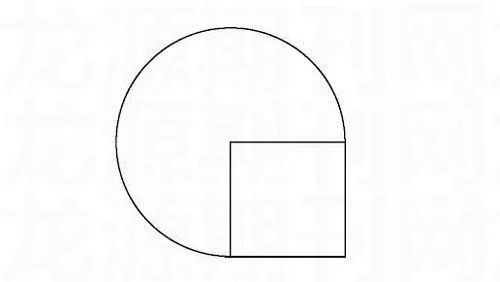
　　例如，学习了“圆的面积”之后，让学生解决这样一道题：已知下图中正方形的面积是8平方厘米，求圆形的面积。由于受思维定势的影响，许多学生认为要求圆形的面积，就必须找出它的半径，而图中圆的半径即正方形的边长，为此陷入了沉思：到底哪个数的平方才等于8呢？真是百思不得其解。这时教师轻轻问道：“图中正方形的面积与圆的半径有什么关系？”一语道破天机，学生的思路顿时豁然开朗：正方形的面积就是圆的半径的平方，求圆的面积只要3.14×8就可以了！
　　在学生的思维陷入困顿时，正是教师适时的轻轻一问，帮助学生跨过了思维的门槛，让他们“柳暗花明”，成就了课堂的精彩。
　　二、学生思维无序时的追问——厘清思路
　　追问是对事物的深刻挖掘，是逼近事物本质的探究，是引导学生思维条理化的纽带，是促进学生思考的催化剂。在学生思维陷入杂乱无序的状态时，教师的适时追问可以引导学生逐步厘清思路，促进其学习水平的提高。
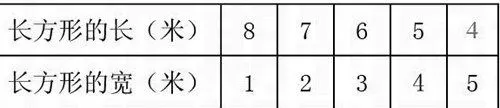
　　例如，“解决问题的策略——一一列举”的例题：“王大叔用18根1米长的栅栏，围成一个长方形羊圈，有几种不同的围法？”在分析题中所含信息之后，教师让学生探索有哪些不同的围法并进行交流。一个学生汇报：“我们围成的长方形分别是长7米、宽2米，长5米、宽4米，长8米、宽1米，长6米、宽3米，长4米、宽5米。”教师问道：“大家觉得这几种围法对吗？有没有什么问题？”面对这些杂乱的排列，学生纷纷表示不同意见。教师追问：“你们有什么好的办法可以做到既不重复又不遗漏？请动手试一试。”学生再次尝试之后，得到了下表中的结论：
　　学生在探索的过程中实际已经体会到或者不自觉地运用了一一列举解决问题的策略，但其表述是无序的。教师通过引导学生对不同列举方法进行比较，使学生体会到有序列举的好处：不重复、不遗漏，感悟到这一策略的价值。这样，学生的思维从无序到有序，从混沌走向清晰，思维能力有效提高。
　　三、学生思维粗浅时的追问——引向深入
　　追问的价值在于探明学生的思维状态，促进思维能力的提升。由于受年龄特点、知识水平的限制，学生的思维活动往往会浮于表面。课堂上，教师在学生思考粗浅处牵一牵、引一引，适当地进行深层次的追问，引领学生不断地探索，激发、启迪学生思维，帮助学生学会知识的延伸，以此促进学生思维逐步走向成熟。
　　例如，在教学“倍数和因数的意义”时，学生通过用12个同样的小正方形摆一个长方形得出算式：3×4=12、2×6=12、12×1=12。教师先以“3×4=12”为例说明3、4、12这三个数的关系：12是3的倍数，12也是4的倍数，3和4都是12的因数；接着让学生从另外两个算式中任选一个说说三个数之间的关系。由于有例子可以模仿，学生说起来毫不费力，对倍数和因数意义的理解似乎告一段落了。这时教师问道：“你觉得哪个算式说起来比较拗口？”一个追问引发了学生的思考，促使学生发现：12是12的倍数，12也是12的因数，使学生对一个数的倍数和因数的特点有了初步认识。教师再次追问：“从以上算式中你发现什么？”把学生的思维由机械模仿引向理性思考，使学生领会在乘法算式中积分别是两个乘数的倍数，两个乘数分别是积的因数，进一步提升了学生的认识水平。
　　在这个片段中，教师的两次追问层层递进，成为不断深化学生思维的“铁锹”。第一次追问“你觉得哪个算式说起来比较拗口？”实际上是把学生的目光聚焦到探索倍数和因数的特点中去。教师有针对性地进行第二次追问“从以上算式中你发现什么？”就把学生的发现推向了完整建构的理性境界。实践证明，教师的有效追问，可以是由表及里的引导，把学生的思维引向纵深；也可以是由此及彼的引导，把学生的思维引向广阔空间，从而提升学生的思维，促进学生的发展。
　　四、学生思维闪现亮点时的追问——渐入佳境
　　数学是思维的体操，数学课堂应是教师和学生、学生和学生之间启迪智慧的场所。课堂上当学生思维闪现亮点时，教师的追问是引导学生进一步探索的“钥匙”，也是提升学生思维高度的“云梯”。随着问题的产生，学生往往会作出相应的思考反应，从而让学习“渐入佳境”。
　　例如，教学“圆的认识”时，教师用课件出示三辆小车，分别是方轮子、椭圆轮子和圆轮子，让学生猜一猜：哪辆小车跑得快？为什么？这个新奇有趣的情景充分调动了学生的学习兴趣，他们很快就得出了结论：“方轮子和椭圆轮子的小车开起来会上下颠簸，圆形轮子的小车开起来不会颠簸，所以圆轮子的小车开得快。”教师并不急于利用这一结论导入新课，而是以问题启迪学生的智慧：“是不是圆轮子的小车就一定不会颠簸呢？”学生肯定地回答：“是！”教师出示了一辆车轴不在圆心的小车模型，进行演示后再次问道：“要使这辆小车的轮子不颠簸，车轴必须装在哪儿？你能找到这个位置吗？”然后让学生动手操作，观察发现圆的有关知识。
　　在以上教学过程中，学生发现“圆轮子的小车开得快”这个结论时，其思维已经出现亮点，此时导入新课未尝不可。教师通过进一步追问“是不是圆轮子的小车就一定不会颠簸呢？”有意为学生的探究活动设置障碍，让他们产生认知冲突，引发他们寻找圆心的求知欲。这样，以有价值的问题引领学生的操作活动，促使学生在探索活动中不断演绎精彩，真正体现教学的真实与深刻、丰富与生动。
　　苏霍姆林斯基说：“教育的技巧并不在于能预见到课的所有细节，而在于根据当时的具体情况，巧妙地在学生不知不觉中做出相应的变动。”有效追问源于教师正确的教学理念、灵活的教学机制。学生获得的将不仅仅是扎实的基础知识、过硬的基本技能，还有能力的形成、思维的提升以及对个性品质的锤炼。让课堂上的有效追问从偶然走向常态，从有痕走向无痕正是我们一线教师的不懈追求。
　　
　　（作者单位：福建省柘荣县城关小学）
　　
　　（责任编辑：张欣）