Sharp Weighted Estimates for a Class of n-dimensional Hardy-Steklov Operators∗

ZHENG QING-YU AND SHI SHAO-GUANG

(Department of Mathematics,Linyi University,Linyi,Shandong,276005)

Sharp Weighted Estimates for a Class of n-dimensional Hardy-Steklov Operators∗

ZHENG QING-YU AND SHI SHAO-GUANG

(Department of Mathematics,Linyi University,Linyi,Shandong,276005)

In this paper,we study one class ofn-dimensional Hardy-Steklov operators which has important applications in the technical analysis in equity markets. We establish their weighted boundedness and the corresponding operator norms on both Lp(Rn)and BMO(Rn).

Hardy-Littlewood average,Hardy-Steklov operator,BMO

1 Introduction

Let a function w(x)≥ 0,x∈[a,b]with 0＜ a＜ b,be given.Then for a measurable function f:Rn→C,the n-dimensional weighted Hardy-Steklov operators which we study are de fi ned as

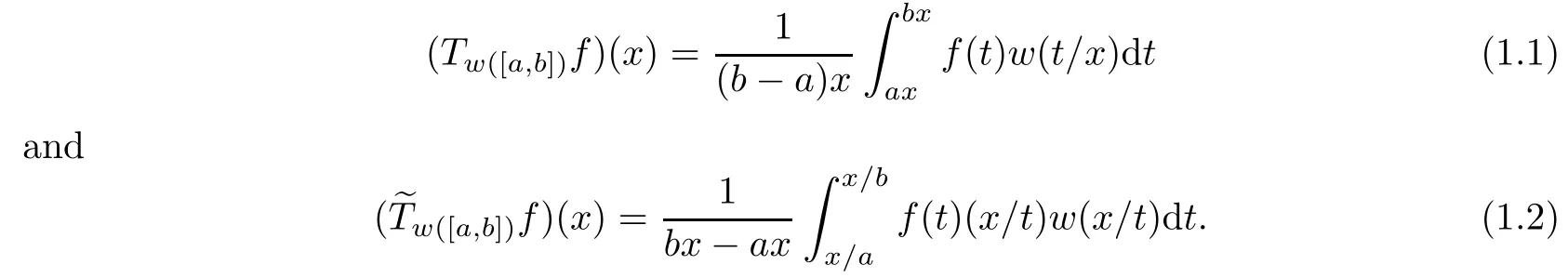
When n=1,(1.1)and(1.2)become the classical Hardy-Steklov operators(HSO).

De fi nition 1.1[1]We call an operator

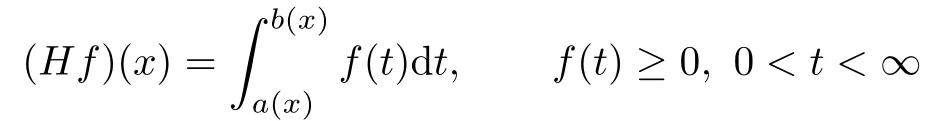
an HSO if the functionsa(x)andb(x)satisfy

The corresponding moving averaging operator of HSO is de fi ned by

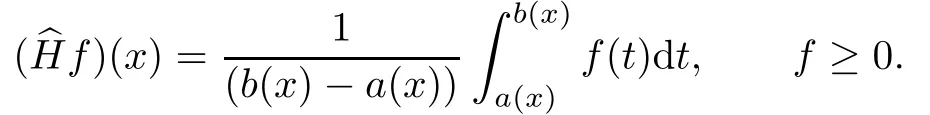
This operator in its various forms is of considerable importance to the technical analysts in the study of equity markets.These technical analysts try to predict the future of the stock price or the future of an equity market solely on the base of the past performance of the stock price or market valuation,respectively.

The study of Tw([a,b])andseems to be of interest as it is related closely to the Hardy-Littlewood maximal operators in harmonic analysis(see[2])and technical analysis in the study of equlity markets(see[1]).For example,if we make the change of variable t′=t/x,then(1.1)and(1.2)become

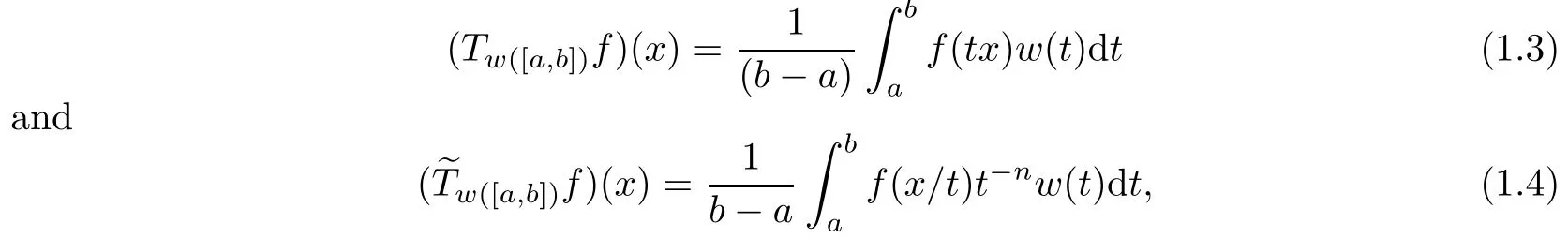
In what follows,for each number λ＞0 and cube Q⊂Rn,let λQ be the cube whose measure has λ|Q|,and whose center is the same as that of Q.For the standard work on BMO(Rn),we refer the reader to[6],[7],[9]and[10].

Inspired by the work in[1],[4]and[7],we study the norm estimates of Tw([a,b])andin Section 2.

2 Main Results

We first establish the boundedness of Tw([a,b])on Lp(Rn).

Theorem 2.1Letw≥0,1≤p≤∞.Then the following two statements are equivalent:

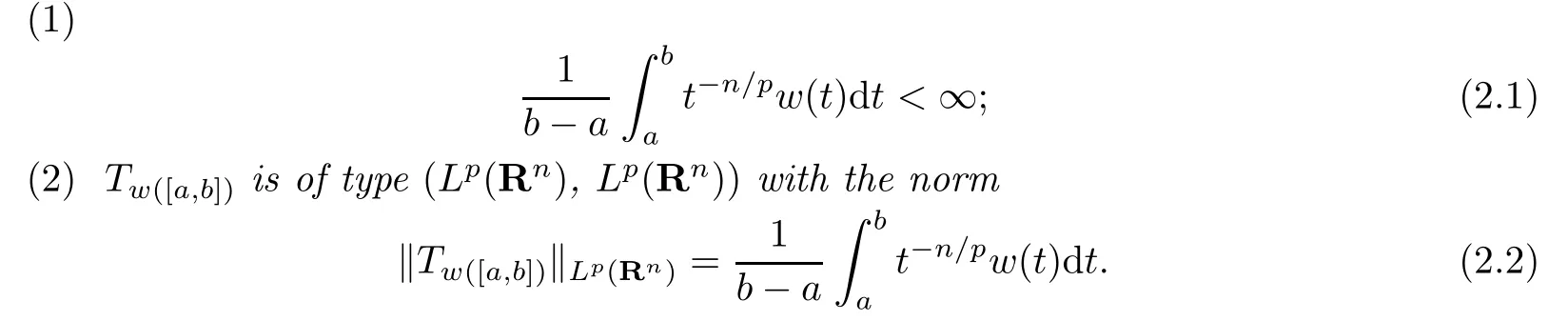
Proof.We only need to consider p∈[1,∞)for the case p=∞ is trivial.Suppose that (2.1)holds.It is sufficient to show that there exists a constant C＞0 such that

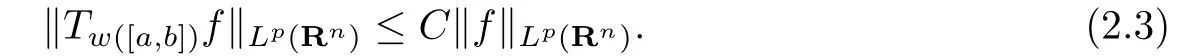
An application of Minkowski’s inequality yields

which shows(2.3).

We are now in a position to show the converse.If Tw([a,b])is a bounded operator on Lp(Rn),then there exists a constant C＞0 such that

Applying the inequality(2.4)to fε,by an elementary integral calculation we have

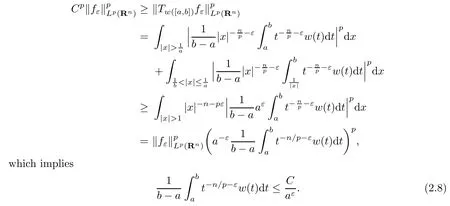
We get(2.1)by letting ε→0.

When(2.1)is true,Tw([a,b])is a bounded operator on Lp(Rn),so we further get

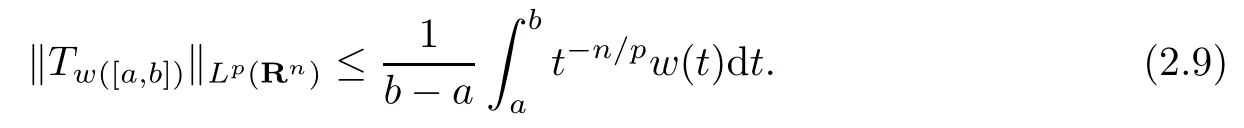
In order to deduce(2.2)from(2.1),we assume otherwise that(2.2)were not true.A use of (2.9)derives that there is a positive number k such that

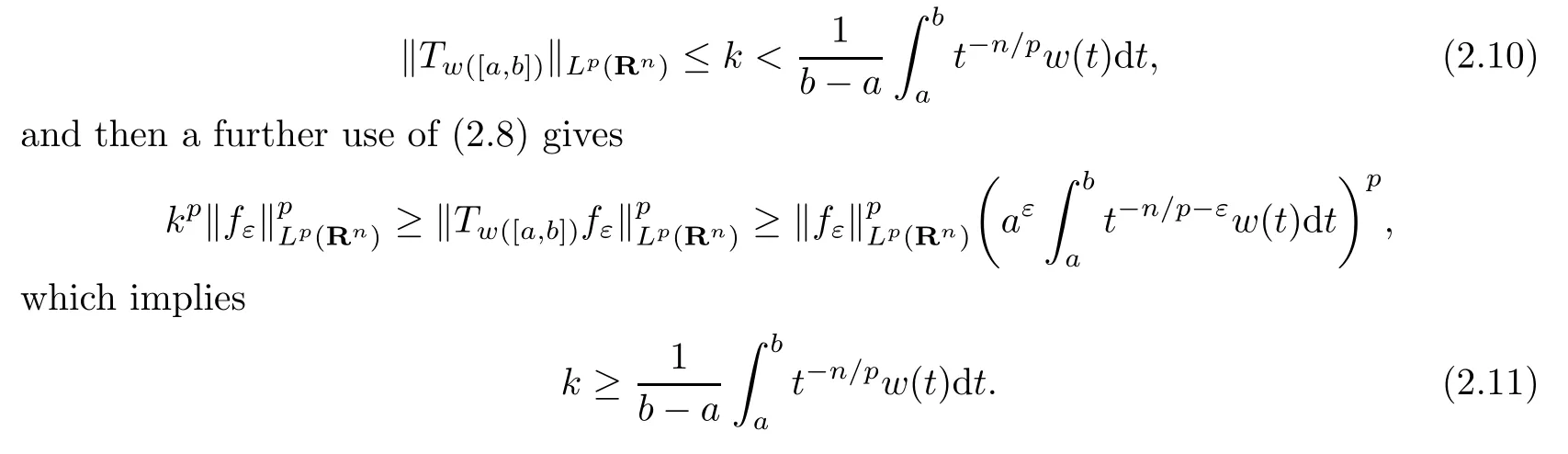
Obviously,the inequality(2.11)contradicts(2.10),so we get(2.2)which completes the proof of Theorem 2.1.

Next,we deal with the boundedness of T on BMO(Rn).

Theorem 2.2Letw≥0,1≤p≤∞.Then the following two statements are equivalent:

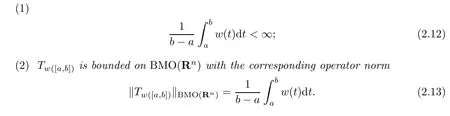
Proof.Assume that(2.12)holds.If f∈BMO(Rn),then for any cube Q we apply the Fubini’s theorem to obtain the equalities

[1]Kufner,A.and Persson,L.E.,Weighted Inequalites of Hardy Type,World Scienti fi c Publishing,Co.Pte.Lte,NJ,2003.

[2]Stein,E.M.,Harmonic Analysis:Real-Variable Methods,Orthogonality,and Oscillatory Integrals,Princeton Univ.Press,Princeton,NJ,1993.

[3]Hardy,G.H.,Note on a theorem of Hilbert,Math.Z.,6(1920),314–317.

[4]Xiao,J.,Lpand BMO bounds of weighted Hardy-Littlewood averages,J.Math.Anal.Appl., 262(2001),660–666.

[5]Zheng,Q.Y.and Fu,Z.W.,Lipschitz estimates for commutators of n-dimensional fractional Hardy operators,Comm.Math.Res.,25(2009),241–245.

[6]Fu,Z.W.,Liu,Z.G.,Lu,S.Z.and Wang,H.B.,Characterization for commutators of ndimensional fractional Hardy operators,Sci.China(Ser.A),50(2007),1418–1426.

[7]Fu,Z.W.,Liu,Z.G.and Lu,S.Z.,Commutators of weighted Hardy operators,Proc.Amer. Math.Soc.,137(2009),3319–3328.

[8]Bennett,C.,Devore,R.A.and Sharpley,R.,Weak L∞and BMO,Ann.Math.,113(1981), 601–611.

[9]Carton-Lebrun,C.and Fosset,M.,Moyennes et quotients de Taylor dans BMO,Bull.Soc. Roy.Sci.Lige,2(1984),85–87.

[10]Fe ff erman,C.,Characterizations of bounded mean oscillation,Bull.Amer.Math.Soc., 77(2002),587–588.

Communicated by Ji You-qing

42B25,42B99

A

1674-5647(2011)04-0343-06

date:Sept.19,2010.

The NSF(10901076,10931001)of China.