巨灾债券的精算定价模型评析

谢世清

(北京大学经济学院,北京 100871)

巨灾债券,通常简称CAT bonds,是一种保险连接证券 (insurance linked securities),其付息或者还本与巨灾事件发生与否相连,即只有当巨灾发生且造成损失满足触发条件时,债券投资者才会损失利息或本金。作为一种把保险风险转移到资本市场的新型投资工具,巨灾债券兼具金融产品和保险产品的特性,因此其定价较普通公司债券要复杂得多。巨灾债券的定价既是巨灾债券的核心技术与难题,也是其得以成功发行的关键。

目前国内对巨灾债券的理论定价模型研究较少,仅有少数学者对此进行了初步尝试。田玲、向飞 (2006)[1]比较分析了风险定价框架下的LFC模型、Wang两因素模型和Christofides模型。陆珩(2006)[2]尝试了在不完全市场框架下基于代表性代理模型的巨灾债券定价模型。田玲、张岳(2008)[3]讨论了巨灾债券定价的影响因素和阐述了基于债券合成的巨灾债券定价方法。本文旨在从保险精算定价的角度对巨灾债券的四个主要理论定价模型进行系统评析。

一、Kreps模型

传统的保险精算定价模型一般首先收集客观的损失数据,然后计算出期望损失 E(L) (Expected Loss),再加上风险承担RL(Risk Load)以及各类费用支出 E(Expenses),则可以计算出巨灾债券的价格P(Premium),即

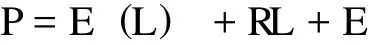
其中的关键是如何计算出风险承担。通常采用标准差风险附加原则,即风险承担RL=风险附加乘数λ＊损失标准差σ。如果不考虑费用支出 (E=0),价格P可简化为:

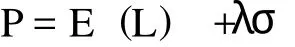
Kreps(1999)[4]从再保险合同定价的投资等价原理出发,考察了一年期单次支付的再保险合同的定价问题。设保险的初始价格为P,风险附加为RL,rf为无风险国债利率,A为再保险公司未收到保费时的初始资产,F为再保险公司的初始投资额,即F=P+A,期望损失为E(L),则再保险合约的价格可以表示为:

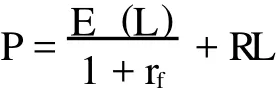
假设目标投资收益率为y,则根据投资等价原理,其现金流期望必须满足如下等式:

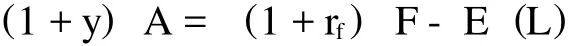
从上面两式中可以进一步求解得出风险附加为:

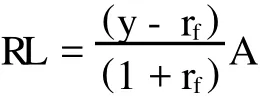
此外,对现金流期望等式取方差有:Aσy=σL,代入上式中可知:

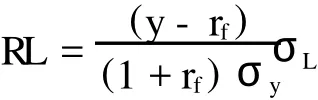
将以上风险附加的表达式代入再保险合约的价格中可得:

Kreps模型的优势首先在于清晰地说明了风险附加部分是利率、目标收益率等因素在内的函数,其次,Kreps模型提出了标准差风险附加的保险精算定价方法,从而为以后的四种主要巨灾债券理论定价模型奠定了基础。但该模型存在着两大缺陷:其一、不能有效反映巨灾损失分布的重尾特征;其二、无法计算各细分风险层次交易价格。正是由于这些缺点,保险界不得不在标准差风险附加模型基础上寻求新的替代模型。

二、LFC模型

LFC模型是由美国Lane Financial公司总裁Morton Lane根据对巨灾债券市场价格的经验观察所提出来的 (Lane,1998)[5]。该模型认为巨灾债券的价格由巨灾期望损失加上期望超额收益两部分组成。第一、巨灾期望损失E(L),即巨灾损失强度的概率加权平均值E(L)=ΣipiLi;第二、期望超额收益 (Expected Excess Return,EER)用以衡量由于巨灾的重尾性质所产生的风险溢价。这样,巨灾债券价格可表示为:

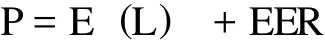
Lane(1999)[6]假设巨灾损失发生概率,即第一美元损失概率为 PFL (Probability of First-dollar Loss),条件期望损失幅度CEL(Conditional Expected Loss)为E(L)/PFL,则期望超额收益 (EER)可以表示为PFL和CEL的函数,即EER=f(PFL,CEL)。

Lane(1998)认为可以用Cobb-Douglas生产函数来估算EER,则有:

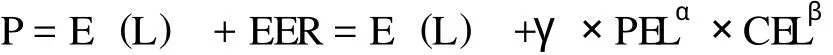
上述风险承担EER计算公式是Cobb-Douglas生产函数在巨灾风险定价中的应用。如同生产函数刻画了生产时对劳动力和资本之间的权衡关系一样,该式也体现了投资者在巨灾损失频率和损失程度之间的权衡关系,即给定相等可能损失性,投资者将偏好更低的损失程度;另一方面,在损失程度相等的情况下,投资者将偏好更低的损失频率。

值得注意的是,α,β,γ是需要根据市场数据来估计确定的三个参数。Lane(2000)[7]运用1999年发行的16只巨灾债券的数据,经过回归分析可得到上述参数的估计值α=49.46%,β=57.41%, γ=55%。一旦确定好这些参数,即可较容易地计算出巨灾债券的价格。作为一个实证模型,LFC模型利用已发行的债券的相关经验数据,预测未来进入市场的债券价格的参考范围。但其缺点也是明显的:第一、未能有效地反映债券二级市场实际价格的周期性变化;第二、也未能吸收巨灾债券标的风险的季节性变化。

三、Wang转换模型

Wang转化模型基于通过观测到的实际巨灾债券的价格对原始巨灾债券分布进行调整,以获得更加准确的巨灾风险分布函数 (Wang,1995)[8]。设S(x)=Pr{X>x}为理论巨灾风险的生存函数,即巨灾损失X超过x的发生概率,故整个巨灾的期望损失为E[X]=(x)dx。巨灾再保险一般采取将巨灾风险分割成不同层次,x(a,a+h)表示风险层次为 (a,a+h]的巨灾风险,相应的赔付函数为:

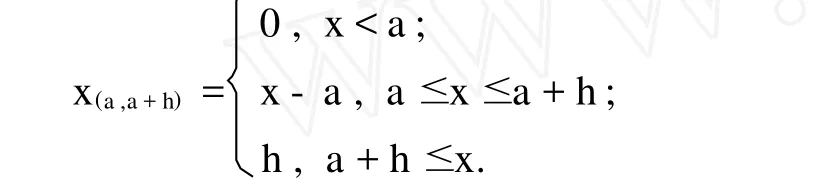
那么,对应于该巨灾风险层次的期望损失可表达为:

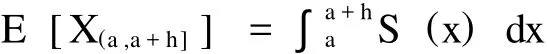
当h较小时,巨灾债券理论价格E[X(a,a+h]≌S(a) ×h近似成立。令实际观测到的巨灾债券价格为E＊[X],则S＊(a) ≌E＊[X]。由于实际价格中加入了风险溢价,即有

(a,a+h](a,a+h]S＊(a)>S(a),我们可以将实际债券价格看作是调整后生存函数的精算值。

令S＊(x)为变换后的巨灾风险生存函数,即S＊(x) =g(S(x)),其中g(0) =0,g(1) =1。Wang(1995)提出的比例风险转换 (proportional hazards transform,PH)具有如下形式,即S＊(x) = (S(x))1-λ,0≤λ≤1。

由于衡量风险厌恶水平的夏普比率能较好地模拟正态分布的巨灾风险,Wang(2002)[9]将夏普比率测度从正态分布资产推广到更加普遍的一种形式,即常用的比例风险转换。经过Wang转换后的巨灾风险生存函数如下所示:

综上所述,不难推导出Wang转换模型下的巨灾债券定价公式为:

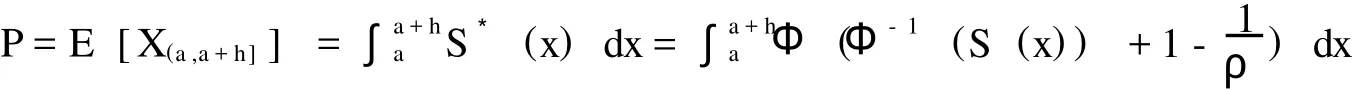
Wang转换模型的最大优点在于将风险溢价加入到期望损失中,并允许价格随着市场特征,如个人风险厌恶水平ρ变化而改变,从而更好地反映实际巨灾风险的概率分布。必须注意,Wang转换模型假设风险的概率分布是已知确定的,而事实上人们总是通过有限的经验数据估计概率分布,这样总是存在参数不确定性问题。后来发展的Wang两因素模型将对这一问题进行修正。

四、Christofides模型

Christofides模型基于Wang提出的比例风险转换模型,通过两次近似处理推导出更为简洁高效的巨灾债券理论价格。图1代表了一个典型巨灾债券的生存函数与附加个人风险厌恶水平的比例风险Wang转换后的函数曲线。其中生存函数曲线S(x)下方面积为巨灾债券的期望损失E(L),比例风险转换曲线S＊(x)= (S(x)1/ρ,ρ≥1与生存函数曲线S(x)之间的面积差为巨灾债券价格中的风险承担,或者是期望超额收益EER。

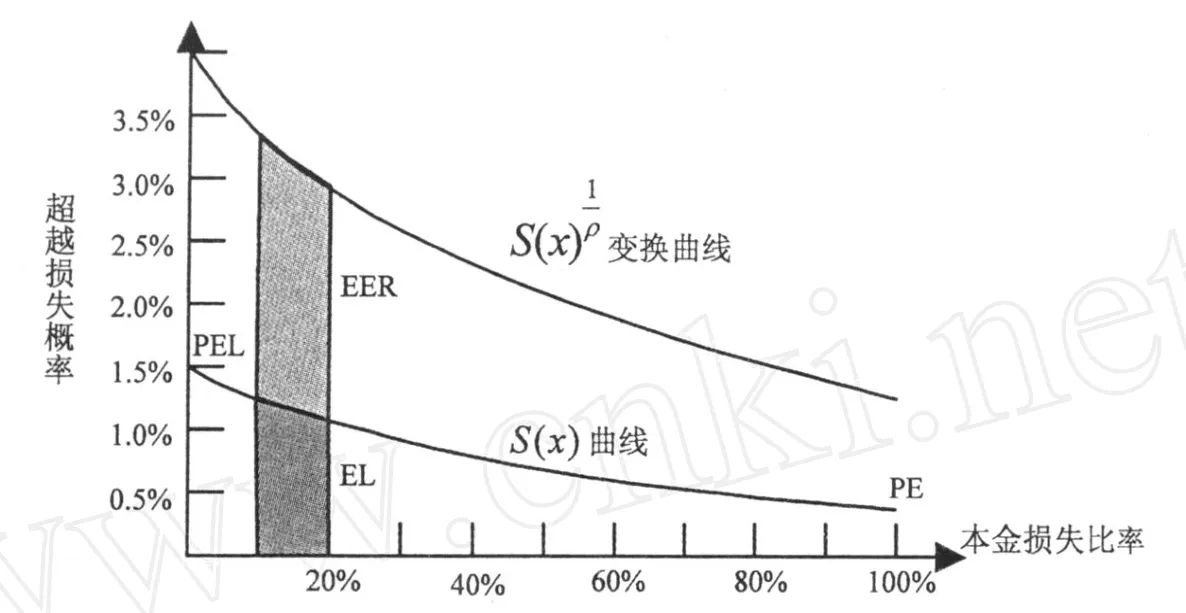
图1 生存函数曲线与考虑到风险厌恶水平后的Wang转换曲线

首先,Christofides(2004)[10]把生存函数S(x)作了第一次近似处理,即用简单的指数衰减函数来刻画生存函数分布:S(x)=αe-βx,其中α,β为需要估算的参数。从生存函数中我们可以发现:(1)第一美元损失概率PFL为S(0)=αe-β×0=α;(2)本金耗尽概率是S(1)=αe-β;那么,没有考虑风险厌恶水平ρ的期望损失E(L)可计算为:

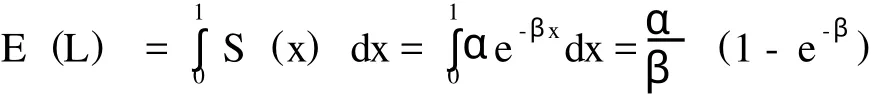
根据第一美元损失概率PFL和期望损失E(L),我们可以对巨灾风险的分布进行近似拟合估算。由于估算出来的指数生存函数可能与本金耗尽率不相吻合,因此可利用已发行的巨灾债券的经验数据估计出风险厌恶水平ρ,从而更好地模拟出巨灾风险分布。在对上述α,β,ρ参数进行估算的基础上,Christofides模型下巨灾债券价格可表示为:

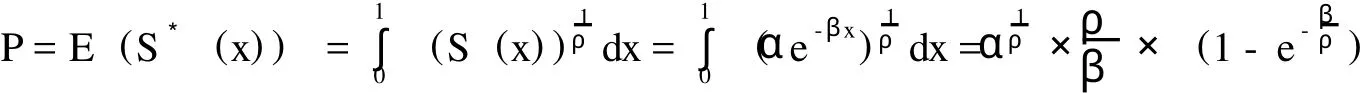
第二,在β较小时,Christofides对上式进行第二次近似处理可得:

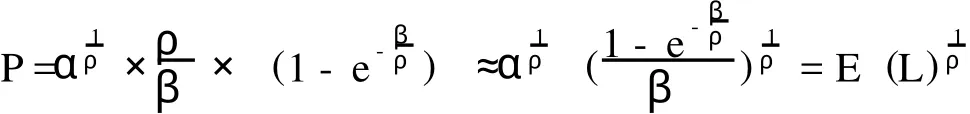
此外,考虑到期望损失E(L)可表达为第一美元损失概率PFL和条件期望损失幅度CEL的乘积,则巨灾债券的价格还可表述为:

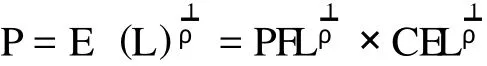
Christofides模型的最大优点在于其对Wang转换模型下计算表达式进行了数学技术上的简化处理,使定价计算更为简单高效,且不会对原有Wang转换模型定价的精确性造成实质性损害。其不足之处在于与Wang转换模型一样,没有考虑参数不确定性问题。

五、Wang两因素模型

Wang转换模型从概率变换上对巨灾债券定价模型进行了调整,而Wang两因素模型则是在Wang转换模型的基础上,对参数不确定性作了进一步改进 (Wang,2002)[11]。Wang转换模型假设资产的收益服从标准正态分布,与现实中巨灾风险的“重尾”特征不符。因此,Wang(2004)[12]用k自由度的学生t分布来替代标准正态分布以更好地描述未知参数的重尾特征。对参数不确定性进行调整后的分布密度函数如下:

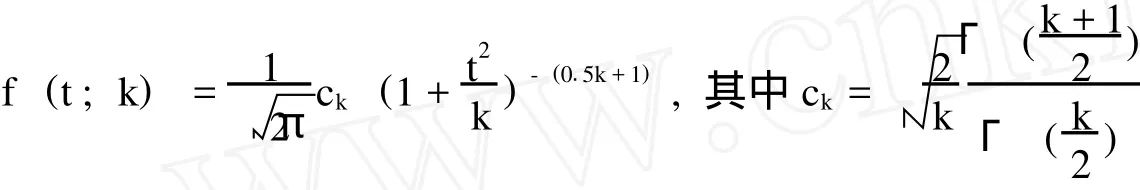
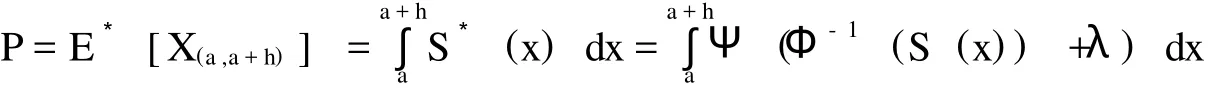
Lane(2000)、Christofides(2004)和Wang(2004)分别对1999年的16只巨灾债券的交易数据进行了实证研究。其分析思路大体一致,都是先获取市场整体定价水平下的参数估计值,再代入原有数据得到模型价格。Wang(2004)利用Wang两因素模型对上述数据进行研究确定出最优参数为λ=0.453,k=5,并发现LFC模型、Christofides模型和Wang两因素模型与实际发行价格标准误差平方分别约为0.41%、0.44%和0.22%。因此,Wang两因素模型较LFC模型和Christofides模型都更加精确。

考虑上述参数的不确定性,并经Wang概率分布转换后的两因素模型的生存函数为:

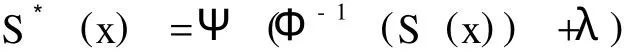
其中Φ为标准正态分布函数,Ψ (.)为t分布,λ为价格市场风险或者夏普比率。

那么,对于风险层次为 [a,a+h]Wang两因素模型下的巨灾债券定价可表达为:

六、四种精算定价模型的比较分析

作为巨灾债券四种常用定价模型,LFC模型、Wang转换模型、Christofides模型和Wang两因素模型,都沿用了传统保险精算的定价思路,运用计量方法估算影响价格的重要因素来定价。不难看出,它们在发展上也具有一定的内在逻辑延续性,是一个不断总结经验和逐步加以改进的过程。表1对这四个模型的共同点和不同点进行了比较分析。

先看共同点:第一,四个模型都是基于传统保险精算定价原理,将巨灾债券价格分为巨灾期望损失和风险附加两部分,都基于Kreps模型所提出的标准差风险附加的保险精算定价方法。所不同的是,LFC模型直接计算风险溢价,而后三者通过概率变换直接实现了风险溢价向风险调整溢价的转换,风险附加部分被隐藏在了计算公式之中。

第二,都不同程度地考虑了巨灾分布的重尾特征,并试图通过各自的风险度量指标进行描述。四个模型都认为传统的风险度量指标夏普比率或标准差难以适应于非对称的巨灾保险风险,因此需要引入相应的、新的风险度量指标进行修正。

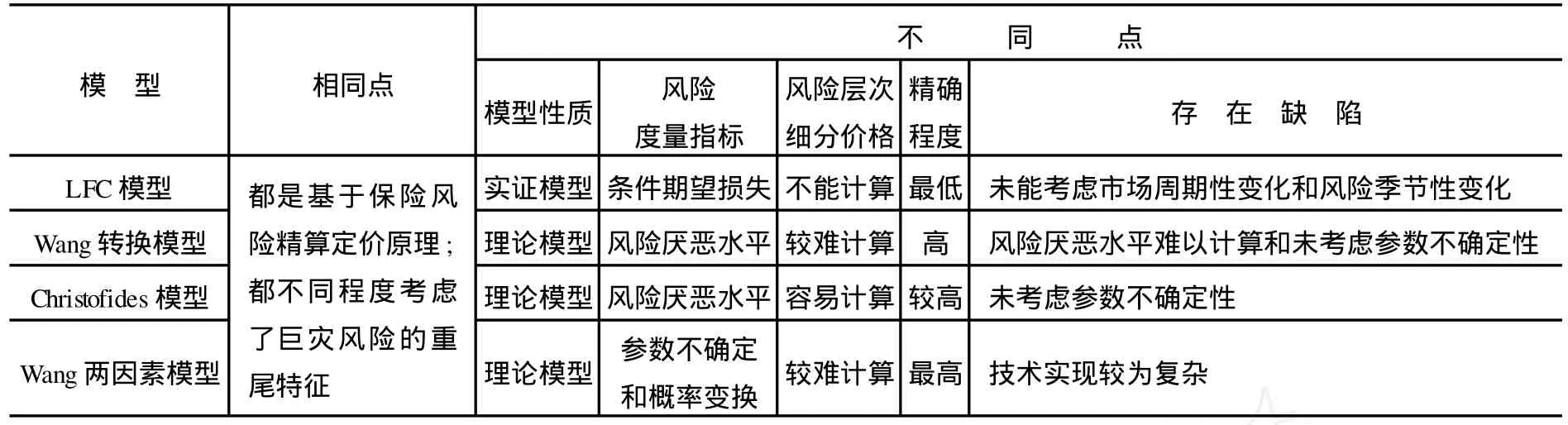
表1 四种精算定价模型的比较分析

再看不同点:第一,模型性质不同。LFC模型属于实证模型,来自于对巨灾债券市场的直接观察与提炼,并没有从理论的角度加以推导模型变量之间的函数关系。后面三个模型属于理论模型,主要基于Wang对资本风险和保险风险统一定价的理论研究,以及Christofides关于系统性风险和非系统性风险的理论定价研究。

第二,风险度量指标不同。LFC模型用条件期望损失来度量偏斜分布的巨灾风险;Wang转换模型和Christofides模型则着重考察市场上的风险厌恶水平;Wang两因素模型主要通过对参数不确定性和概率变化来刻画巨灾风险。

第三,风险细分层次价格可否计算。LFC模型无法计算巨灾风险细分层次上的债券价格,后三者均可以计算,只是技术实现复杂程度有所不同。具体而言,Christofides模型较Wang转换模型和Wang两因素模型计算更为简单,只需要考虑风险厌恶系数。

第四,精确程度不同。总体而言,Wang两因素模型在精确程度上要优于Wang转换模型; Wang转换模型要优于Christofides模型;Christofides模型则优于LFC模型。

第五,存在缺陷不同。LFC模型的主要缺陷在于面临着市场周期性变化和风险的季节性变化; Wang转换模型中风险厌恶水平难以计算;Christofides模型缺乏对参数不确定性因素的考虑;Wang两因素模型则面临着各参数的估算和巨灾概率分布变换在技术实现上更加复杂。

七、结 语

自汉诺威再保险1994年首次成功发行巨灾债券以来,巨灾债券发展迅速,现已成为巨灾保险市场上最为活跃,接受程度最高的巨灾保险连接证券,并对传统的再保险进行了有力补充。巨灾债券的迅速发展离不开其定价模型的不断改进。在传统再保险的Kreps期望-方差定价理论基础上,巨灾债券的定价模型发展出四个常用精算定价模型:LFC模型、Wang转换模型、Christofides模型和Wang两因素模型。

通过对上述四个主要精算定价模型的回顾与分析,本文发现,巨灾债券定价模型的发展实质上是在传统债券定价理论的基础上,不断引入自然风险特征以及市场特征的一个逐步完善过程。虽然其定价模型尚存在一定的缺陷,但日趋成熟的巨灾债券市场也间接说明了巨灾债券精算定价模型的合理性。如何进一步合理描述巨灾风险的特性、参数的不确定性以及市场不完全等特征将是未来巨灾债券定价模型发展的主要方向。

[1]田玲,向飞.基于风险定价框架的巨灾债券定价模型比较研究[J].武汉大学学报,2006,(2).

[3]田玲,张岳.巨灾风险债券定价研究的进展评述[J].武汉大学学报,2008,(5).

[4]Kreps,Rodney.Investment-equivalent Reinsurance Pricing[M],in Van Slyke,O.E.(Ed.),Actuarial Considerations regarding Risk and Return in Property-Casualty Insurance Pricing,Casualty Actuarial Society,Alexandria,VA,pp.77-104,1999.

[5]Lane,M..Price,Risk and Ratings for Insurance-linked Notes:Evaluating Their Position in Your Portfolio[J],Derivatives Quarterly,1998 (Spring).

[6]Lane,M..Risk Cubesor Price,Risk and Ratings[J],Journal of Risk Finance,1999(Fall).

[7]Lane,M..Pricing Risk Transfer Transactions[J],ASTIN Bulletin,Vol.30,pp.259-293,2000.

[8]Wang,Shuan.Insurance Pricing and Increased Limits Ratemaking by Proportional Hazards Transforms[J],InsuranceMathematics&Economics, Vol.17,Issue 1,pp.43-54,1995.

[9]Wang,Shuan.A Classof Distortion Operators for Pricing Financial and Insurance Risks[J],Journalof Risk and Insurace,Vol.67,No.1,15 -36,2000.

[10]Christofides,Stavros.Pricing of Catastrophe Linked Securities[C],ASTIN Colloquium International Actuarial Association,Brussels,Belgium, 2004.

[11]Wang,Shaun.Pricing of Catastrophe Bonds[M],Alternative Risk Strategies,Risk Press,2002.

[12]Wang,Shuan.Cat Bond Pricing Using Probability Transforms[C],Special Issue Insurance and the State of the Art in Cat Bond Pricing, Geneva,2004(January).