栅格翼气动特性研究现状及应用前景

郭江涛，陆飞龙，王 柯，刑存震

（1.南京理工大学 能源与动力工程学院，南京210094；2.辽沈工业集团有限公司，沈阳110045）

栅格翼气动特性研究现状及应用前景

郭江涛1，陆飞龙1，王 柯1，刑存震2

（1.南京理工大学 能源与动力工程学院，南京210094；2.辽沈工业集团有限公司，沈阳110045）

介绍了国内外关于栅格翼的研究现状，从气动特性、数值模拟、实验研究、结构优化等方面进行了总结.分析了栅格翼相对于平板翼的优势与不足，对栅格翼的应用前景进行了展望.

栅格翼；气动特性；现状；减阻

栅格翼是一种不同于传统舵面的升力面和控制面，作为一种新型弹翼，它是由众多的栅格壁镶嵌在边框内形成的.栅格壁在边框内的布局最基本、最常用的有两种：一种是框架式，一种是蜂窝式，如图1所示.蜂窝式栅格壁又分为正置和斜置两种.目前应用比较多的是斜置壁与边框成45°角的蜂窝式栅格翼［1］.

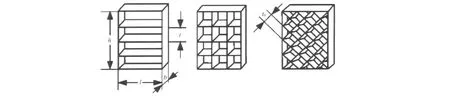
图1 栅格翼的几种主要布局形式

栅格翼的主要几何参数有翼弦b、翼展l、翼高h和格间距t0.翼弦b是指翼剖面内彼此相距最远的两点之间的距离；翼展l是指栅格翼两侧壁之间的距离；翼高h是指沿栅格翼轴线度量的上端和下端格壁之间的距离；格间距t0是指两相邻栅格相应点之间的距离.

由于栅格翼突出的结构特点和良好的空气动力特性，引起世界各国的高度重视，俄罗斯、美国、德国以及中国等都加强了栅格翼理论研究和实验研究工作.

1 国外研究现状

苏联最早成功地将栅格翼用作联盟号宇宙飞船救生逃逸系统的稳定翼面.之后，俄罗斯首次在R－77中程空空导弹上采用四片栅格尾翼舵面，取代了常规舵面（如图2所示），而且以后在很多型号的导弹上使用.美国对栅格翼在导弹上的应用给予了很高的评价，近年来连续发表了多篇研究报告［2－3］，还将它成功应用在许多超音速导弹和一些小直径炸弹上.针对栅格翼的控制特性，国外的研究主要有以下几个方面：

1.1 数值模拟及计算研究

在数值计算中，由于栅格翼的特殊结构，网格生成一直是研究的重点和难点.在研究初期，主要采用非结构网格，对计算精度有很大影响.Karl Orthner等对栅格翼在跨音速阶段的气流壅塞现象进行了研究，并采用分区方法生成多重结构网格［4－5］.Lin Herng等采用在二维平面分区生成栅格翼结构网格的方法，把栅格翼结构网格拓展至三维区域进行研究［6］.James De－Spirito等采用数值模拟方法对栅格翼作为鸭式布局组合体尾翼的滚转控制性能进行了研究，并对带栅格翼和平板翼鸭式布局导弹进行了数值计算，然后将计算结果与风洞实验数据作了比较，计算出的流场显示，低超音速下鸭舵下洗尾流涡在导弹右舷形成低压区，产生法向诱导力，诱导力随速度增加而减小，当攻角足够大后，尾涡不再影响下风面的尾翼，表明低超音速栅格翼比平板翼的滚转控制更有效［7］.Despirito J等对Fournier E Y的栅格翼实验模型进行了数值计算，从单独栅格翼上的计算结果和流场来看，由于在大攻角时背风翼的根部出现流动分离，导致部分翼面的相对攻角为负值，这正好解释了Fournier E Y实验中两个垂直的翼几乎不产生法向力增量的原因［8］.

图2 R－77中程空空导弹

1.2 实验方法研究

对栅格翼的升阻特性和铰链力矩特性及栅格翼翼身组合体与平板翼翼身组合体气动特性的异同，国外进行了大量的实验研究.Simpson G M等指出，在大的攻角和马赫数下栅格翼可以提供比平板翼更好的横向稳定性，拥有更高的控制效率；相对于十字型布局的平板翼水平方向的翼面提供所有的纵向稳定性而言，栅格翼水平方向翼面只提供70%的纵向稳定性；跨音速阶段栅格翼将产生气流壅塞现象，并使控制效率降低［9］.William David Washington等对常规单面翼和栅格翼两种布局进行了实验研究，发现在超音速阶段，栅格翼的布局会产生比单面翼更大的法向力［10］.Gregg Abate等通过风洞实验研究了跨音速阶段栅格翼的气流壅塞现象对气动特性的影响，指出法向力、俯仰力矩及压心在 Ma＝0.8左右时都有下降［11］.Gregg L Abate等进行了常规单面翼和栅格翼的自由飞实验，发现栅格翼布局的轴向力系数与单面翼布局的轴向力系数相比，亚音速时大约大了1倍，超音速时超过了50%；测得了第一临界马赫数，但这个临界马赫数的出现是否与模型尺度有关还需要进一步研究［12］.Fournier E F做了与自由飞实验模型相似的两种布局的风洞实验，论证了两种布局气动特性与马赫数和攻角的关系，还将栅格翼与光弹进行了比较，指出两个水平的栅格翼产生了几乎100%的法向力增量［13］.

2 国内研究现状

我国自20世纪90年代初开始了对栅格翼的研究，并且已将栅格翼成功应用在神舟号宇宙飞船逃逸飞行器上.栅格翼是保证逃逸飞行器静稳定性的特殊装置，当逃逸飞行器在39km高度以下的大气中出现应急情况启动逃逸系统时，为了保证逃逸飞行器的气动稳定性，需要靠4块展开的栅格翼将逃逸飞行器气动压心后移，实现稳定飞行，因此栅格翼是决定逃逸方案成功实现的关键因素之一.栅格翼及其释放机构已成功地通过了CZ－2F逃逸飞行器零高度实验和最大速度头实验评估，并参加了从神舟一号到神舟七号飞船的发射任务.国内对栅格翼的研究主要有以下方面.

2.1 理论分析方法

由于栅格翼的结构形式复杂，以及各栅格壁之间存在着严重的相互干扰，流动性受扰动气流的马赫数、相对间距、攻角、栅格翼剖面形状和相对厚度的影响，故用求解方程的方法计算它的空气动力特性有一定的困难.比较可行的是依据它在亚音速、跨音速和超音速流中的绕流特性，采用不同的计算方法来计算栅格翼的气动力.

亚音速时，所有栅格壁均处于同等状态下，具有相同的空气动力特性；从侧壁脱出的自由涡系本身是一个均匀分布的涡面，并具有均匀不变的涡强；自由涡产生的下洗具有良好的均匀性.鉴于以上特点，采用涡格法计算栅格翼空气动力.涡格法就是将栅格翼的附着涡系和自由涡系用许多离散的马蹄涡来代替，将栅格翼的每块栅格壁沿展向和弦向划分成许多网格，在每个网格上布置一个马蹄涡，其附着涡放在网格的1／4弦线上，控制点取网格的3／4弦线的中点处，如图3、图4所示.沈遐龄等就采用这种方法进行实验，并得到了比较满意的结果［14］.可以认为，亚音速情况下采用涡格法能满足工程设计的需要，是一种非常有效的计算方法.

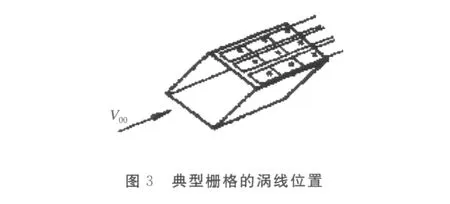
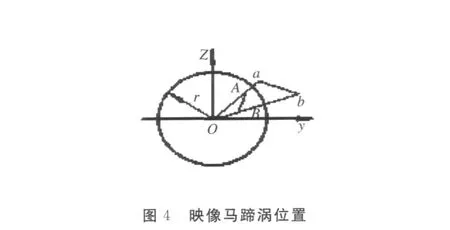
跨音速时，栅格翼可看作许多有着相同来流的小网孔的集合体，而每个小网孔内的气流可以看作一维流动.据此可以建立跨音速复杂流动区域的空气动力特性计算方法.

超音速时，栅格壁上将出现激波，并且激波会在壁面上反射；当来流马赫数大于第三临界马赫数时，反射就会消失，此时不能再用基于等墒流的一维通道假设研究栅格翼内的气体流动.当忽略激波的交叉影响和末端效应时，用激波膨胀波法计算栅格翼的气动力，对于下边框外面的流动，用线化理论修正三维流动效应.沈遐龄等采用激波膨胀波法和线化理论相结合的方法进行空气动力计算，并与实验结果进行比较，二者吻合较好，进一步证明了激波膨胀波法的可操作性［15］.

通过相关计算和研究可知，栅格翼是具有空间分布自由涡系的升力面系统，亚音速时很适合采用基于升力面理论的涡格法来计算其法向力特性.在跨音速条件下，栅格翼可看作许多有着相同来流的孤立小网孔的集合体，而每个网孔内的气流可看作一维流动，据此可采用一维流动理论计算其空气动力特性.在超音速流中，忽略交叉影响和末端效应，用激波膨胀波法计算栅格壁上的法向力，也可反映出波系之间及波系与壁面间的相交与反射情况.

2.2 网格技术与数值模拟

由于栅格翼特殊的蜂房结构，大大增加了与弹身网格对接的难度，即使这种栅格翼勉强生成网格，网格质量也得不到保障.因此，寻找一种合理的网格方法，成为CFD亟待解决的问题之一.

刘刚等采用结构、非结构混合网格的办法，在弹体和栅格翼的物面附近区域，生成适合粘性计算的大长宽比的结构网格，弹体网格和栅格翼网格之间采用非结构网格进行填充，以满足非结构网格和结构网格交界面的完全对接；对不同舵偏角下的栅格翼构形进行数值模拟，并与实验结果进行对比，验证了该数值模拟方法的可靠性［16］.

吴晓军等对多种不同外形单栅格的气动特性进行了数值计算，对单个栅格的外形进行了选型研究，然后采用混合网格技术进行了数值模拟.为了更好地模拟边界层，他们采用分块对接加“O”型网格技术，精细模拟附面层内的流动状况，在每一个子区域单独生成网格，然后在每个子区域连接面处实现网格完全对接，每一个子区域网格采用无穷插值方法生成计算网格，用椭圆方程优化.所采用混合网格是在多块对接网格的基础上，在栅格翼附近挖出一块，用非结构网格填充，形成龙形网格，这样可以使栅格上的网格点数没有延伸到整个流场，从而使计算的总网格规模大大降低［17］.

王斌等采用非结构直角网格欧拉方程求解器来降低网格生成的工作量，并采用自适应网格来提高计算精度［18］.非结构直角网格是一种用先空间后物面的方式来一次性生成计算所需网格的网格生成技术，与结构网格和非结构网格相比，采用笛卡尔网格和网格自适应技术具有简单、省时、自动化程度较高、激波捕捉精度高的优点.这种方法对于复杂物面形状依赖度也较低，尤其适用于外形优化计算的研究.

通过研究，我们可以发现，混合网格技术结合了结构网格和非结构网格各自的优点，提高了网格生成的质量；同时由于不考虑结构网格的空间对接，减小了网格生成的难度，节省了大量计算机内存和计算时间.这种技术是目前求解栅格翼飞行器亚、跨、超音速气动特性比较理想的方法之一，为采用CFD研究栅格翼气动特性提供了便利.

在数值模拟方面，姚琰等用Fluent对单独栅格翼的流体动力特性进行数值模拟，并将计算结果与空泡水洞实验结果进行比较，得到栅格翼失速舵偏角较大，弦长比单面翼小，铰链力矩小［19］.当栅格翼作为潜射导弹水下控制面时，所需舵机功率小，这也为栅格翼在潜射导弹上的应用提供了广阔的前景.张亮等采用数值模拟法与工程算法对高超音速栅格翼进行研究，分析了在高超音速下栅格翼激波干扰对前缘钝度的敏感性以及栅格翼热流分布产生的影响.其研究结果表明，在相同栅格间距下，产生激波干扰的第三临界马赫数随栅格翼前缘钝度的增加而增加，传统的尖前缘栅格翼理论不适用于钝化前缘外形，因此在高超音速理论中常采用等效楔的方法改善计算结果；激波干扰在栅格翼表面会产生局部的高热区域，但此热流峰值与前缘驻点相比仍较小，对栅格翼热防护也无额外影响；随着飞行器性能的不断提升，如何合理地评估热防护对栅格翼在高超音速下的应用显得十分关键，这也成为下一步材料学中研究的主要问题之一［20］.

吴晓军等运用数值模拟的方法研究了栅格长宽比对栅格气动特性的影响.其研究结果表明：在所选择的长宽比范围内，长宽比对阻力的影响不大，而对法向力有明显的影响，并且栅格存在一个最佳的长宽比，此时产生的法向力最大，因此设计长宽比时应尽量使得栅格下壁面的前缘斜激波打在上壁面，而上壁面的前缘斜激波不打在下壁面上；在模拟的马赫数下，栅格边框厚度、栅格片的厚度、栅格截面是影响栅格翼阻力的关键设计参数［21］.通过对栅格翼边框剖面形状和栅格片厚度进行进一步的设计权衡和优化研究，可知减小格片厚度、尖前缘、后尖后缘等，有可能使阻力进一步减小.

2.3 结构优化及实验研究

陆中荣等通过采用氢气泡法和丝线法在水洞和风洞中进行实验研究得知，栅格翼是具有空间自由涡系分布的多面翼；由于栅格翼的几何特性，保证了流动的均匀性；栅格壁之间的相互影响，使栅格壁表面的逆压梯度减小，以致大迎角下分离滞后，分离程度也减弱［22］.这些结论是在低速流动中得到的，对于高速流动则需要进一步研究与探索.

栅格翼虽具有升力和滚转控制优势，但其阻力较大，这也是需要解决的主要问题.邓帆等为了减小阻力，设计了3种不同后掠方式的栅格翼，并采用数值模拟的方法研究了其减阻效果，其中两种栅格翼模型是前缘局部后掠的，另一种栅格翼是整体后掠的，如图5所示.他们对不同后掠栅格翼的研究表明，栅格翼无论是整体后掠还是前缘局部后掠，都可有效减阻，而栅格翼前缘局部后掠是一种更为有效的减阻方式，比整体后掠有更好的减阻特性，相比较栅格中心为尖点后掠的方式而言，栅格交接点后掠在减小波阻方面更加有效.这种结构设计也为栅格翼的减阻提供了一种新的途径和方法［23］.

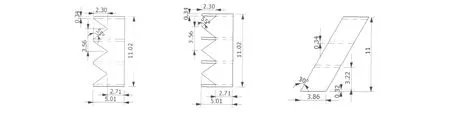
图53种栅格翼模型工程图（单位：mm）

格宽翼弦比是影响气动特性的一个重要参数.陈少松等采用实验方法对3中不同格宽翼弦比的栅格翼在亚、跨、超音速下进行了气动分析，结果表明，栅格翼格宽翼弦比对阻力影响不大，而对于法向力系数，存在一个合理的格宽翼弦比，使得法向力特性在整个亚音速、跨音速、超音速范围内最好；随着格宽翼弦比的减小，栅格翼的弦向压心增加，铰链力矩系数、滚转力矩系数也增加［24］.在这里陈少松等是采用增加弦长的方法来减小格宽翼弦比.如果保持弦长不变，仅改变栅格间距的大小来减小格宽翼弦比，其气动特性的变化规律则有待进一步研究.

为了研究栅格翼边框尺寸、边框截面形状、格栅形式等对栅格翼阻力的影响，陈少松等采用风洞实验方法对不同形状栅格翼进行了气动分析，结果表明，栅格翼的边框特别是边框剖面形状对栅格翼的阻力影响较大，因此，选择合适的栅格翼边框剖面形状可以有效地减小栅格翼的阻力；栅格翼的茎厚度对阻力系数的影响远不如边框的影响大，因而为保证栅格翼的强度，可以适当增加栅格翼的茎厚度；用减少栅格数目的方法来减小栅格翼阻力，会降低栅格翼升力面，进而影响栅格翼的升力特性，因此这不是一个有效的减阻手段［25］.另外，如何使边框几何形状与栅格尺寸、翼茎厚度、几何形状进行合理搭配，使阻力降到更低，这也是需要考虑的问题.陈少松等还对不同栅格翼组合体模型进行了风洞实验研究，并与平板翼翼身组合体空气动力数据进行比较，发现栅格翼的阻力比平板翼大得多，网格数越多，阻力越大，在超音速下，展长相同时斜置密网格栅格翼的升力特性与俯仰力矩特性均好于平板翼和稀网格栅格翼，削尖栅格翼的边框可以有效减少栅格翼的阻力［26］.

3 栅格翼的优势与不足

栅格翼作为一种创新性的升力面，理论和实验研究都证明了其性能在许多方面都优于单面翼，有自身独特的优势，主要表现在以下方面：

（1）栅格翼可以在相当大的攻角和马赫数范围内正常使用，并且具有良好的升力特性.这是因为栅格翼的栅格具有某种理顺气流的作用，在亚音速时减弱了气流的分离，在较高超音速时由于栅格壁的作用使绕流互不干扰.

（2）铰链力矩很小.这是由于栅格翼为一立体升力系统，翼弦很短，压心变化范围小，从而对飞行器舵机及伺服机构的设计要求降低很多.

（3）栅格翼能在体积比较小的情况得到较大的翼面总升力面.体积相等时，翼面总升力面积大，则升力大.在超音速下，栅格翼的升力可比单面翼大很多.

（4）适合大攻角下的飞行控制.因为栅格翼失速角比单面翼大，且在攻角大于失速角时升力的降低也比单面翼缓慢得多，所以在大攻角飞行时仍然有控制力产生.

（5）栅格弦向尺寸小，可折叠安装在弹体上，不会加大弹体的外形尺寸.在一些情况下，可以在空气动力作用下自动打开，十分有利于导弹的存放、运输和发射.栅格翼还可以用作舰艇的稳定翼，在一般情况下折叠于船体上，在遇到风浪时将其打开，以稳定船体.

然而，栅格翼也有自身突出的缺点，主要是：

（1）栅格翼的结构复杂，制造工艺难.

（2）亚音速时其气动特性比平板翼低，阻力比较大；跨音速段，由于壁面之间的波系干扰，使升力相对减小，当攻角加大以求得到较大的升力时，其阻力也相应增加.

（3）隐身性相对较弱，这也成为妨碍栅格翼在制导兵器上应用的关键问题之一.

4 结 语

由于栅格翼具有弦向尺寸小、铰链力矩小、失速攻角大和升力特性好的特点，特别适合作为导弹的全动舵面，因此可以采用较小功率的舵机，使导弹产生更大的法向过载，利于导弹的控制.栅格翼的弦向尺寸较小，可以使弹翼折叠在弹身上，特别适用于管式发射、机载悬挂，也便于这类导弹的结构设计.

随着对栅格翼气动特性研究的不断深入，特别是在减阻增升技术、制造工艺技术上的突破，栅格翼必将在兵器上得到更加广泛的应用.

［1］ 陆中荣，沈遐龄，童自力，等.栅格翼空气动力特性的计算与分析［J］.北京航空航天大学学报，1996（5）：575－580.

［2］ William David，Washington，Mark S Miller.Grid Fins：A New Concept for Missile Stability and Control［R］.New York：AIAA，1993：35.

［3］ James Despirito，Harris L Edge，Paul Weinacht，et al.CFD Analysis of Grid Fins for Maneuvering Missiles［R］.New York：AIAA，2000：391.

［4］ Karl Orthner.Aerodynamic Analysis of Lattice Grid Fins in Transonic Flow［D］.New York：AFIT／GAE／E，2004.

［5］ Montgomery C Hughson，Eric L Blades，Gregg L Abate.Transonic Aerodynamic Analysis of Lattice Grid Tail Fin Missiles［R］.New York：AIAA，2006：3651.

［6］ Lin Herng，Huang Juan－chen，Chieng Ching－Chang.Navier－Stokes Computations for Body／Cruciform Gridfin Configuration［R］.New York：AIAA，2002：2722.

［7］ James DeSpirito，Milton E Vaughn Jr，W David Washington.CFD Investigation of Canard－controlled Missile with Planar and Grid Fins in Supersonic Flow［R］.New York：AIAA，2002：4509.

［8］ William David Washington，Pamela F Booth，Mark S Miller.Curvaure and Leading Edge Sweep back Bffects on Grid Fin Aerodynamic［R］.New York：AIAA，1993：3480.

［9］ Simpson G M，Sadler A J.Lattice Control：A Comparison with Conventional，Planar Fins［C］.Sorrento，Italy：RTOAVT Symposium on‘Missile Aerodynamics’，1998.

［10］ William David Washington，Mark S Miller.Grid Fins：A New Concept for Missile Stability and Control［R］.New York：AIAA，1993：35.

［11］ Gregg Abate，Gerald Winchenbach，Wayne Hathaway.Transonic Aerodynamic and Scaling Issues for Lattice Fin Projectiles Tested in A Ballistics［C］.Interlaken，Switzerland：19th International Symposium of Ballistics，2001.

［12］ Gregg L Abate，Ralf P Duckerschein，Wayne Hathaway.Subsonic／Transonic Free－flight Tests of a Generic Missle with Grid Fins［R］.New York：AIAA，2000：937.

［13］ Founder E Y.Wind Tunnel Investigation of Grid Fin and Conventional Planar Control Surfaces［R］.New York：AIAA，2001：256.

［14］ 沈遐龄，王丽丽.栅格翼和机身组合体的气动特性计算与分析［J］.北京航空航天大学学报，2001，27（1）：54－56.

［15］ 沈遐龄，陆中荣，童自力，等.栅格翼与机身发动机组合体的气动特性计算［J］.北京航空航天大学学报，1996，22（6）：727－732.

［16］ 刘刚，肖中云，江雄，等.混合网格方法在栅格翼数值模拟中的应用研究［J］.空气动力学学报，2007，25（2）：277－230.

［17］ 吴晓军，马明生，邓有奇，等.结构／非结构混合网格数值模拟栅格翼［J］.空气动力学学报，2009，27（4）：419－424.

［18］ 王斌，张卫民.栅格翼气动特性数值研究［J］.战术导弹技术，2011（2）：15－19.

［19］ 姚琰，毛鸿宇.栅格翼流体动力特性数值模拟［C］.西安：第十二届全国计算流体力学会议，2004.

［20］ 张亮，王淑华，姜贵庆.钝化前缘对栅格翼激波干扰与热流分布的影响［J］.宇航学报，2010，31（2）：324－328.

［21］ 吴晓军，陈红全，邓有奇，等.栅格绕流数值模拟研究［J］.空气动力学学报，2009，27（1）：78－82.

［22］ 陆中荣，王海文.栅格翼绕流特性的实验研究［J］.流体力学实验与测量，2002，16（1）：21－26.

［23］ 邓帆，陈少松.栅格翼外形特征对减阻影响的研究［J］.实验流体力学，2011，25（3）：10－15.

［24］ 陈少松，张建叶.格宽翼弦比对栅格翼气动特性的影响［J］.南京理工大学学报，2005，29（6）：693－696.

［25］ 陈少松，徐琴，王福华，等.栅格翼减阻特性研究［J］.流体力学实验与测量，2001（4）：7－11.

［26］ 陈少松，徐琴，王福华，等.栅格翼组合体的超音速气动特性研究［J］.弹道学报，2000，12（2）：50－54.

Current Status and Development Trend on the Aerodynamics Characteristic of Grid Fin

GUO Jiang－tao1，LU Fei－long1，WANG Ke1，XING Cun－zhen2
（1.Nanjing University of Science and Technology，Nanjing 210094；2.Liaoshen Industrial Group Co.，Ltd.，Shenyang 110045，China）

This paper mainly introduced the research status of grid fin at home and abroad.A conclusion of aerodynamic behaviour，numerical simulation，experiment reseach structural optimization is made.The superiority and shortage of grid fin over the traditional planar fin are analyzed.Grid fin prospects of development application is predicted.

grid fin；aerodynamics characteristic；actuality；drag reduction

TJ760.3

A

10.3969／j.issn.1671－6906.2011.06.010

1671－6906（2011）06－0047－06

2011－10－26

郭江涛（1987－），男，河南开封人，硕士生.