通信对抗系统电磁兼容问题数学建模与计算
2011-12-26张传勇丁亚非
张传勇,丁亚非,王 江
(合肥电子工程学院404室,安徽合肥 230037)
通信对抗系统电磁兼容问题数学建模与计算
张传勇,丁亚非,王 江
(合肥电子工程学院404室,安徽合肥 230037)
在对通信对抗系统中的电磁兼容问题进行了分析的基础上,建立了电磁干扰余量数学模型和电磁干扰3要素数学模型。并依据所建立的模型,采集相关数据代入模型进行计算,证明了所建立模型的合理性。
通信对抗系统;电磁兼容;电磁干扰;数学模型
随着电子技术的快速发展,电子设备使用频谱日益展宽,发射功率不断增大,使得电子设备所处的战场电磁环境日趋复杂,电磁斗争日益激烈。通信对抗系统集侦察、干扰、测向及系统的内部通信于一体,其系统的电磁兼容性决定着系统能否发挥预期的作战效能。笔者针对通信对抗系统在电磁兼容问题上的特殊性,对通信对抗系统电磁兼容问题进行了数学建模和数据计算。
1 通信对抗系统电磁兼容问题分析
电磁兼容问题中电磁干扰源、耦合途径、敏感设备,对应于通信对抗系统的发射机、信道、接收机。在通信对抗系统中,既有发射大功率干扰信号的干扰站,又有接收信号的侦察、测向站,同时还有用于发射和接收信号的通信设备。干扰站的干扰信号、通信辐射信号无疑会对侦察设备、测向设备及通信设备接收端产生影响,除此之外还有干扰站的干扰信号对站间通信的影响,通信信号对干扰引导接收的影响,对于整个通信对抗系统而言,配置在电子对抗系统中,雷达对抗系统中干扰站和通信设备也会对通信对抗系统产生电磁干扰。
2 通信对抗系统电磁兼容问题的数学建模
2.1 电磁干扰余量模型
通信对抗系统中,被干扰系统输入端口的干扰电平Pr(f,t,d,p)数学模型为

通信对抗系统内部干扰系统、侦察系统、测向系统、通信系统间的电磁干扰余量模型[1]为
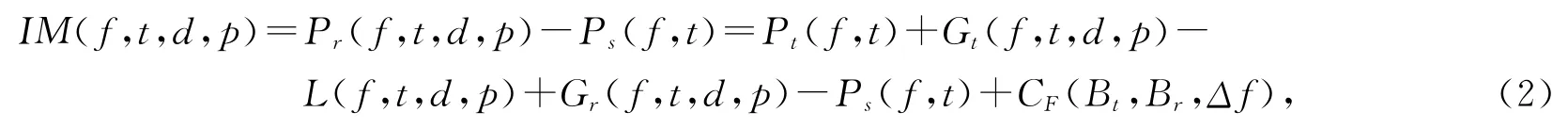
式中:IM(f,t,d,p)为干扰余量,dB;Pt(f,t)为干扰系统发射机在发射频率f 的发射功率,dBm;Gt(f,t,d,p)为干扰系统发射机的发射天线在发射频率f对应接收天线方向的增益,d B;L(f,t,d,p)为干扰系统与被干扰系统之间的电波传播损耗,dB;Gr(f,t,d,p)为被干扰系统接收机的接收天线对应发射天线方向的增益,dB;Ps(f,t)为被干扰系统的敏感度门限值,dBm;GF(Bt,Br,Δf)为计入发射机带宽Bt和接收机带宽Br及发射机发射与接收机响应之间的频率间隔Δf的校正系数,d B。在发射机调谐且Br>Bt时,发射机功率完全被接收,不需校正,在发射机调谐且Br<Bt时,仅接受部分发射功率,其校正系数为CF(Bt,Br,Δf)=10 lg(Br/Bt),在发射机失谐情况下,校正系数为CF(Bt,Br,Δf)=20 lg(Br/Bt)。
若IM(f,t,d,p)>0,则表示通信对抗系统中的干扰系统与被干扰系统存在潜在干扰;
若IM(f,t,d,p)=0,则表示通信对抗系统中的干扰系统与被干扰系统处在临界状态;
若IM(f,t,d,p)<0,则表示通信对抗系统中的干扰系统与被干扰系统能兼容工作。
对于一般系统而言,为保证电磁兼容,干扰余量IM(f,t,d,p)要求小于等于-10 dB。
2.2 干扰发射机模型
发射机工作时除产生规定频段内的射频功率外,还产生若干杂散频率上的发射,这些功率都可能对接收机产生电磁干扰。从通信对抗系统电磁兼容问题考虑,所有的发射机都必须视为潜在干扰源。笔者建立了基于测量数据的基波发射幅度模型和通用谐波发射幅度模型。
2.2.1 基波发射模型[2]
当多台发射机工作在不同调谐频率的测量数据已知的情况下,基波辐射的平均功率和标准偏差δT(fOT)的数学模型为
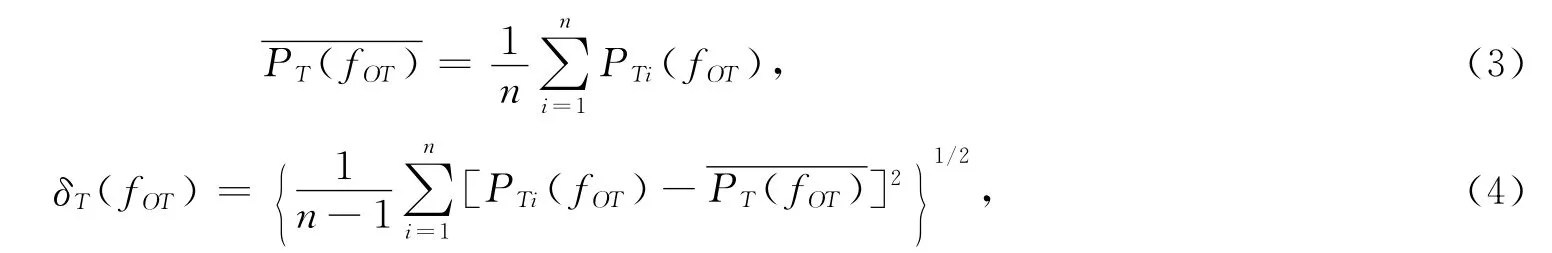
其中:n为采样总数;fOT为基波频率;PTi(fOT)为基波输出功率的各测量值工作在不同调谐频率的发射机的基波功率平均值。
为计算方便,发射功率单位常用dBm,与一般的脉冲峰值功率换算[3]为

2.2.2 谐波发射模型[2]
谐波发射的数学模型为
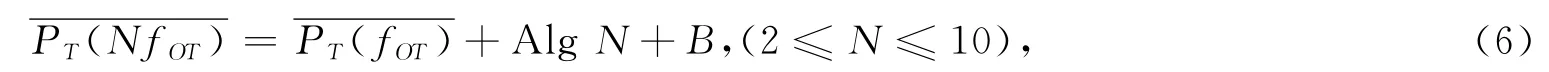
2.2.3 谐波发射模型计算举例
以某VHF干扰站为例,假定工作在发射频率为30~300 MHz,发射功率为1 k W的条件下,从文献[1]中可查A=-80,B=-30,则其发射机二次谐波功率为
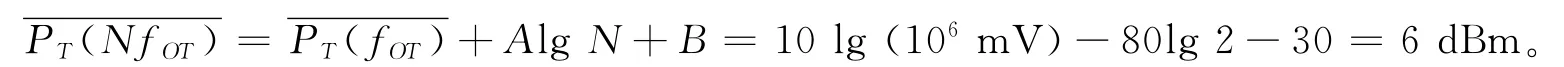
2.3 被干扰接收机模型
通信对抗系统电磁兼容问题中,接收机是敏感设备,其响应描述敏感设备对输入干扰和信号的频率响应。笔者建立了基波敏感度阈值模型和接收机带外干扰平均敏感度阈值模型。
2.3.1 基波敏感度阈值模型
基波敏感度阈值模型为
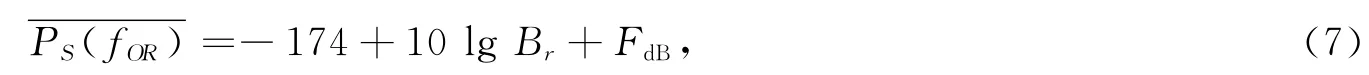
式中:FdB为噪声系数,dB;Br为接收机带宽,Hz。
2.3.2 基波敏感度阈值模型计算举例
某型通信对抗侦察系统接收机的有效带宽为10 MHz,噪声系数是6 d B,则其基波敏感度阈值为
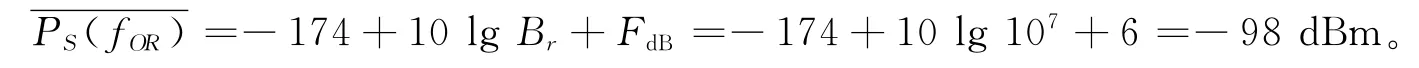
2.3.3 接收机带外干扰平均敏感度阈值模型[1]
没过几分钟,斯坦利和妻子都面色发青,瘫倒在地。亲属们吓坏了,立即叫来了救护车。但悲剧再次重演,斯坦利夫妇均告不治。
接收机带外干扰平均敏感度阈值模型为
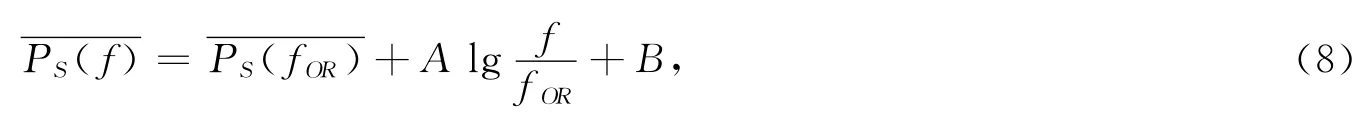
式中:A,B为接收机常数,具体数值一般根据数理统计得出,通常有表1经验结论[1]。
2.4 电波传播损耗模型
在通信对抗系统中,系统天线间的电波传播损耗模型主要有自由空间电波传播损耗模型和egli模型2种。
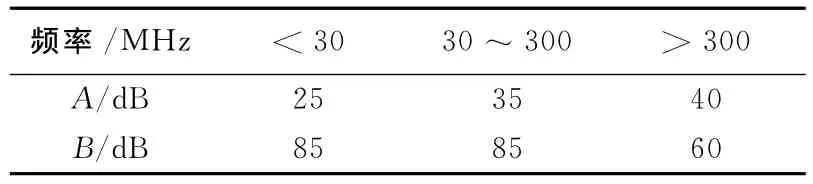
表1 不同类型接收机的A,B平均值
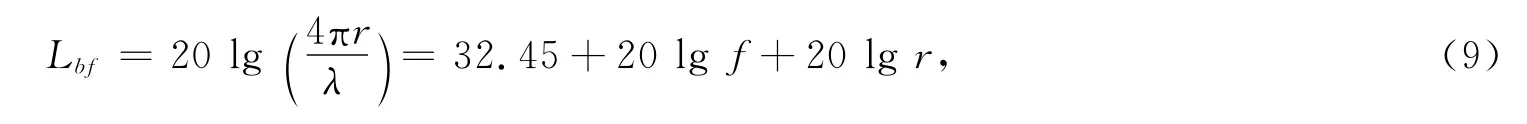
式中:Lbf为电波传播损耗;f为发射机工作频率;r为电波传播距离。
2.4.2 egli模型
egli模型的应用较广,适应性较强,且符合战术超短波系统的通信要求,根据接收天线的不同架高分为2种模型。
当接收天线架高大于10 m时,模型为
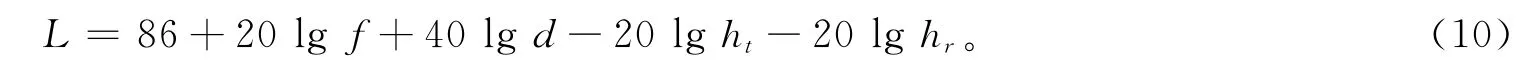
当接收天线架高小于10 m时,模型为
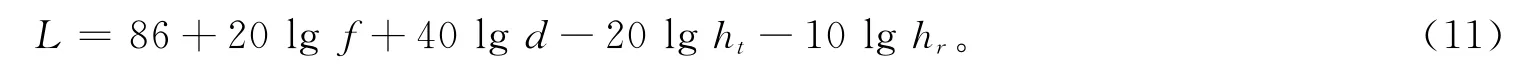
式中:L为路径损耗,dB;f为发射机工作频率,MHz;d为收发天线间的距离,km;ht为发射天线架高,m;hr为接收天线架高,m。
2.4.1 自由空间电波传播损耗模型[4]
自由空间电波传播损耗是指球面波在传播过程中,随着传播距离的增加,能量的自然扩散而引起的损耗,其模型为
3 通信对抗系统电磁干扰的计算举例
以通信对抗系统中超短波通信电台对侦察设备的干扰计算为例,超短波通信电台配置于干扰车上,与侦察设备不在同一地点,空间上有隔离,假定两者距离5 km,按视距计算,超短波通信电台工作频率为200 MHz,侦察设备工作在超短波频段,工作频率为100~500 MHz,超短波通信电台架高10 m,侦察设备架高10 m,依据egli模型,由公式(10)计算得:L=86+20 lg200+40 lg 5-20 lg10-20 lg10=120 d B,超短波通信电台发射功率为10 W,由公式(5)计算得:Pt=10 lg(104)=40 dBm,超短波通信电台和侦察设备两端天线增益按0计,超短波通信电台发射带宽为5 k Hz,侦察设备接收带宽为10 MHz,由于发射带宽小于接收带宽,因此校正系数CF=0。假定超短波通信电台接收机噪声系数为9 dB,依据基波敏感度阈值模型,由公式(7)计算侦察设备输入端敏感度门限值为PS=-174+10 lg 107+9=-95 dBm,依据电磁干扰余量模型,则侦察设备输入端干扰余量由公式(4)计算得:
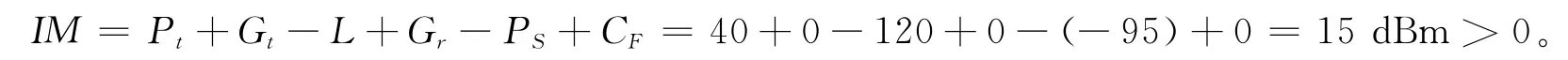
由此判断存在假定条件下,超短波通信电台对侦察设备存在电磁干扰。
上述计算与实际通信对抗系统的干扰情况一致,说明笔者所建立数学模型及分析方法是可行的。
4 结 语
通过以上对通信对抗系统电磁兼容问题的分析和相关数学模型的建立,以及超短波通信电台对侦察设备电磁干扰的计算举例,证明对实际作战运用上研究电磁兼容性有一定指导意义,有利于发挥通信对抗系统的最大作战效能。
[1] 王定华,赵家升.电磁兼容原理与设计[M].成都:电子科技大学出版社,1995.
[2] 胡皓全,杨显清,赵家升.雷达之间电磁干扰预测模型研究[J].电子科技大学学报,2001,30(1):37-40.
[3] DAVID L A.电子战建模与仿真导论[M].吴汉平译.北京:电子工业出版社,2004.
[4] 王铭三.通信对抗原理[M].北京:解放军出版社,1999.
TN975
A
1008-1542(2011)07-0049-03
2011-06-20;责任编辑:张 军
张传勇(1985-),男,山东济南人,硕士研究生,主要从事电子对抗系统建模与仿真方面的研究。
