单原子层磁性纳米带的自旋波谱①

米斌周 庄云飞

(华北科技学院基础部,北京东燕郊 101601)

单原子层磁性纳米带的自旋波谱①

米斌周②庄云飞

(华北科技学院基础部,北京东燕郊 101601)

本文利用量子统计理论的多体格林函数方法计算了单原子层磁性纳米带的自旋波的色散关系。带宽为L的纳米带,其自旋波能谱有L条,自旋波能量随温度的升高而降低。温度接近居里点时,自旋波能量趋于零,可以称之为模式的软化。零温时,准一维纳米带体系的自旋波能量曲线随带宽的变宽而上升,最后趋于二维平面的数值。把单原子层磁性纳米带与单壁磁性纳米管的自旋波能谱做比较,前者的自旋波能量是非简并的,后者是简并的。自旋波能量简并在物理上是由对称性所致,与纳米管相比,纳米带的几何对称性明显降低了。

磁性纳米带;量子自旋模型;格林函数方法;自旋波

0 引言

纳米带由美国佐治亚理工学院王中林研究小组在 2001年首次实验报道[1-3]。随后,人们利用不同的方法制备出了各种半导体氧化物或非氧化物的纳米带状结构[4-8]。纳米带[1-8]具有长方形截面,宽度和厚度在纳米量级,宽厚比较大,长度可达微米或毫米量级,是一种没有缺陷 (例如空缺或断层)的单晶纳米结构[9,10]。这种纳米带状结构有望成为纳米器件的重要基本成分,并且为基础研究和技术应用提供一个良好的机会。关于纳米带的实验[9-13]及理论[14,15]研究,人们已经做了相关的工作。文献[15]利用基于第一性原理的密度泛函理论计算了MoS2纳米带的磁学和电学性质等。2010年,文献[16,17]将量子统计理论的多体格林函数方法应用到了介观领域,分别对磁性纳米管和纳米带的磁学性质进行了完全的量子化描述,加深了人们对于磁性纳米管和纳米带的认识,对实验和进一步理论研究都有一定参考价值。由于格林函数在理论技术上存在的困难以及计算时间的限制,作者只处理了单壁磁性纳米管和单层磁性纳米带。

虽然文献[17]对单原子层磁性纳米带的磁学性质进行了较为详尽的研究,由于篇幅的限制,没有对自旋波谱做深入的讨论。本文在文献[17]研究的基础上,对自旋波谱做一个较为深入的研究。本文利用量子统计理论的多体格林函数方法详细计算和深入讨论了单原子层磁性纳米带的自旋波谱。

1 模型和计算公式

计算模型如图 1所示,单原子层纳米带沿着z轴方向,亦即长度所在的方向看成无限长。宽度所在的方向设为y轴。我们就说纳米带的宽度(简称带宽)为L,即沿着y轴方向的行数 (line)是L。每一个格点上有一个自旋,晶格常数设为a。

图 1 单层纳米带模型图

我们给出体系的海森伯交换哈密顿量为:

其中下标用希腊字母μ表示行数,英文字母i、j指标每行上的格点。例如,μi表示第μ行第i个格点。前两项是海森伯交换作用项,其中第一项表示同一行上格点之间的交换作用,第二项表示相邻行之间的交换作用,这里都只考虑最近邻格点间的交换。第三项是单离子各向异性项。第四项是外场能。本文的数值计算中取:Jμ=100,K2μ=1(μ=1,2,…L),Jμ,μ+1=100,(μ =1,2…,L-1)。所有的参量以及温度都是无量纲的量。

根据Mer min-Wagner定理[18],对于一维或二维各向同性海森伯系统,不存在自发磁化。但是,如果体系引入单离子各向异性,无论它多么小,就会产生自发磁化。文献[17]证实了这一点。定义推迟格林函数:

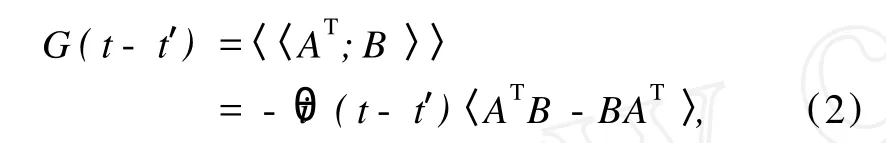
(2)式中的算符向量取为:

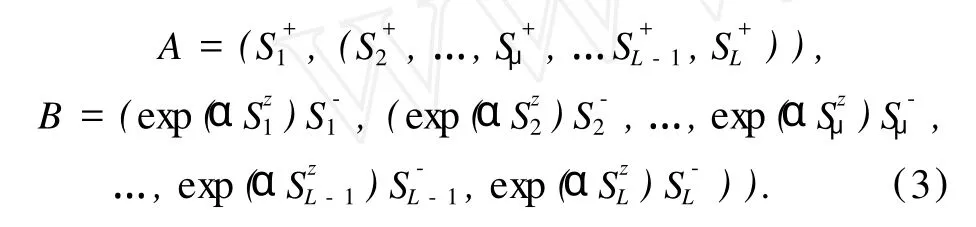
其中α是一个参量。

这里的格林函数是一个L×L矩阵(L阶方阵)。求解格林函数的过程同文献[17],这里不再详细推导,只做简要说明。格林函数的一级极点就是这个系统的自旋波能谱ωτ=ωτ(p)。也就是说,计算系统的自旋波谱就是求 P矩阵[17]的本征值ωτ。

矩阵 P是三对角实矩阵,其非零矩阵元为:

这里,我们用〈〉表示第μ行的磁化强度,用S表示自旋量子数。

要求解 P矩阵[17]的本征值ωτ,为此,必须先求出系统的磁化强度。磁化强度的计算公式同文献[18-20]。

当S=1/2时,即使加上 (1)式等号右边的第三项,即单轴各向异性项,也不显现各项异性[20]。因此,本文只计算S=1时的情况。

2 数值结果和分析

矩阵 P的所有特征值ωv是波矢p的函数,ωv=ωv(p),它就是这个系统的自旋波能谱。现在令Bz=0,计算无外磁场时自旋波的色散关系。色散关系表述为能量ω(p)与波矢p的关系,如图2所示。自旋量子数S=1,计算参数取为:(a)T=0,L=5;(b)T=10,L=5;(c)T=0,L=10;(d)T=10,L=10。计算结果表明,纳米带的自旋波能谱有L条。当带宽L一定时,自旋波能量曲线随温度的升高而降低。这是因为自旋波能量ω(p)正比于磁化强度,温度升高,磁化强度降低,因此元激发的能量也就降低。

图 2 低温下自旋波的色散关系曲线

色散关系表述为能量ω(p)与波矢pa的关系,自旋量子数S=1.计算参数取为:(a)T=0,L=5;(b)T=10,L=5;(c)T=0,L=10;(d)T=10,L=10.

数值计算表明,纳米带在S=1,L=5时的居里温度数值是TC=44.1,图 3画出了接近居里点时自旋波的色散关系曲线。自旋量子数S=1,计算参数取为:(a)T=43,L=5;(b)T=44,L=5.同样可以看出,当带宽L一定时,自旋波能量曲线随温度的升高而降低。并且温度非常接近居里点时,自旋波能量 (或频率)趋于零。由于自旋波能量ω(p)是正比于磁化强度的,接近居里点时,磁化强度趋于零,因此自旋波能量 (或频率)也就趋于零,这个可以称之为模式的软化。

色散关系表述为能量ω(p)与波矢pa的关系,自旋量子数S=1.计算参数取为:(a)T=43,L=5;(b)T=44,L=5.TC=44.1.

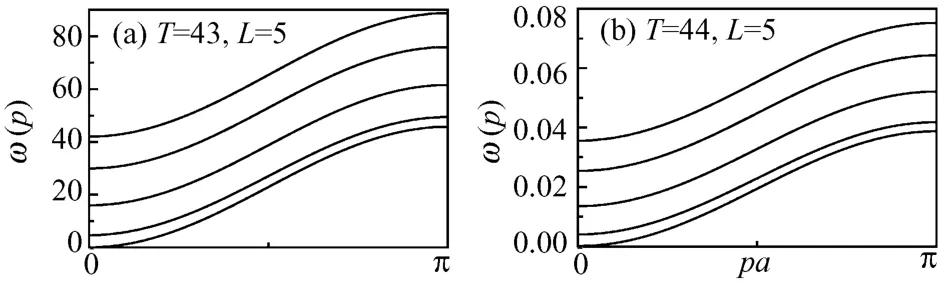
图 3 接近居里点时自旋波的色散关系曲线

下面,我们对纳米带的自旋波谱做一些较为深入的研究和讨论。图 2和图 3画出了L=5或10时,几个温度下的色散关系。从图 2看到,在同一温度下,纳米带越宽,色散关系曲线越密集。这里我们定义能级展宽度Δ为一个波矢处的ω的最大值与最小值之差。分析图 2,纳米带宽度固定时,温度越高,能级展宽度Δ越窄。温度一定时,纳米带越宽,能级展宽度Δ也越宽。如果纳米带的带宽无限增大时,色散曲线会怎样变化?为了简单且能说明问题,我们只计算了L=40,T=0时的色散曲线,如图 4所示。可以看出,这时的色散曲线与图 2(a)、(c)相比,越来越密集,两边的已经连在了一起。如果L再继续增大,趋于无限大,色散曲线会连在一起成为连续谱,量子效应消失。也就是说,纳米带的带宽L越小,量子效应越显著。

另外,分析图 2(a)、(c)和图 4,纳米带在零温时的能级展宽度Δ越来越趋于一个常数 400。为了比较,我们也计算了二维平面在零温时的数值为Δ(2D)=400。我们得到一个结论:零温时,纳米带的宽度L增大,能级展宽度Δ变宽并且逐渐趋于二维平面的数值。这是为什么呢?先从几何结构上分析,纳米带的带宽L趋于无限大时,它的几何形状趋于二维单原子层。再从物理上分析,零温时,系统的热力学涨落肯定为零。对于量子涨落,则与对称性有关。先分析体系哈密顿量的对称性,如果是各向异性,那么量子涨落为零。如果各向同性,那么三维时量子涨落为零。低于三维时,量子涨落是不为零的。换句话说,量子涨落总是有的。只是在三维情况,量子涨落被完全压抑了。各向异性时也可以说量子涨落被完全压抑了,体现不出来。我们现在研究的体系是各向异性的,零温度时体系不存在自旋波能量量子涨落,这似乎与计算结果相矛盾。其实并不矛盾,因为我们在求解格林函数时需要在实空间做傅里叶变换,纳米带和二维平面是有本质差别的。纳米带在一维实空间中 (沿着z轴,波矢记为p)做傅立叶变换,而另一个方向 (y轴)受到限制,能量是分立谱。对于二维平面,在两个方向 (z轴和y轴)做了傅立叶变换,波矢分别记为p和q,都在第一布里渊区 (FBZ)内,能量是连续谱。假若纳米带在受到限制的方向上也存在一个波矢q1,这个波矢只能用带宽L来标识。纳米带的带宽L趋于无限大时,L标识的波矢q1和二维平面的波矢q的差别才会减小。所以零温度时的这种差别是由于纳米带的几何对称性降低造成的,系统并不存在量子涨落。

图 4 纳米带 L=40,T=0时的色散曲线 .

在几何上,纳米带可看成是纳米管切开平展而得到的结构,反过来,如果把纳米带卷起来考虑了两个边界的耦合,就形成了纳米管。几何结构的不同导致了纳米管和纳米带的磁学性质的不同。文献[17]对纳米带与纳米管的自旋波能谱做比较,发现前者的自旋波能量是非简并的,而后者是简并的。纳米带具有镜像对称性(纳米带关于过中间行垂直于它的平面是镜像对称性的),而纳米管的物理图像如同一个救生圈,纳米管除了具有镜像对称性外,还具有旋转对称性。与纳米管相比,纳米带的对称性明显降低了。

3 结论

宽度为L的纳米带,其自旋波能谱有L条,ωv=ωv(p),v=1,2,…L.自旋波能量ω(p)随温度的升高而降低。温度接近居里点时,自旋波能量趋于零。我们研究发现,零温时,准一维纳米带体系的自旋波能量曲线随带宽的变宽而上升,最后趋于二维平面的数值。对单原子层磁性纳米带与单壁磁性纳米管的自旋波能谱做比较,前者的自旋波能量是非简并的,后者是简并的。自旋波能量简并在物理上是由对称性所致,与纳米管相比,纳米带的几何对称性明显降低了。

[1]Z.W.Pan,Z.R.Dai,and Z.L.Wang,Nanobelts of Semiconducting Oxides[J].Science,2001,(291):1947-1949

[2]Z.R.Dai,Z.W.Pan,and Z.L.Wang,Ultra-long single crystalline nanoribbons of tin oxide[J].Solid State Communications,2001,(118):351-354

[3]Z.W.Pan,Z.R.Dai,and Z.L.Wang,Lead oxide nanobelts and phase transformation induced by electron beam irradiation[J].Appl.Phys.Lett,2002,(80):309-311

[4]X.D.Wang,Y.Ding,Christopher J.Summers,and Z.L.Wang,Large-Scale Synthesis of Six-Nanometer-W ide ZnO Nanobelts[J].J.Phys.Chem.B,2004,108(26):8773-8777[5]Y.Jiang,X.M.Meng,J.Liu,Z.Y.Xie,C.S.Lee,and S.T.Lee,Hydrogen-Assisted Thermal Evaporation Synthesis of ZnS Nanoribbons on a Large Scale[J].Adv.Mater.,2003,15(3):323-327

[6]Z.Y.Yuan,J.F.Colomer,and B.L.Su,Titanium oxide nanoribbons[J].Chem.Phys.Lett.,2002,363:362-366

[7]RenzhiMa,Katsutoshi Fukuda,Takayoshi Sasaki,MinoruOsada,and YoshioBando,Structural Features of Titanate Nanotubes/Nanobelts Revealed by Raman,X-ray Absorption Fine Structure and Electron Diffraction Characterizations[J].J.Phys.Chem.B,2005,109(13):6210-6214

[8]R.Q.Song,A.W.Xu,and S.H.Yu,Layered Copper Metager manate Nanobelts:Hydrothermal Synthesis,Structure,andMagnetic Properties[J].J.AM.CHE M.S OC.,2007,(129):4152-4153

[9]J.Zhang,W.Y.Yu,andL.D.Zhang,Fabrication of semiconducting ZnO nanobelts using a halide source and their photoluminescence properties[J].Phys.Lett.A,2002,(299):276-281

[10]J.Zhang,F.H.Jiang,and L.D.Zhang,Fabrication,structural characterization and optical properties of semiconducting gallium oxide nanobelts[J].Phys.Lett.A,2004,(322):363-368

[11]S.X.Mao,M.H.Zhao,and Z.L.Wang,Nanoscale mechanical behavior ofindividual semiconducting nanobelts[J].Appl.Phys.Lett.,2003,83(5):993-995

[12]X.D.Bai,P.X.Gao,and Z.L.Wang,Dual-mode mechanical resonance of individual ZnO nanobelts[J].Appl.Phys.Lett.,2003,82(26):4806-4808

[13]X.D.Li,X.N.Wang,Q.H.Xiong,and Peter C.Eklund,Mechanical Properties of ZnS Nanobelts[J].Nano Lett.,2005,5(10):1982-1986

[14]G.B.Liu,B.G.Liu,Domain structuresof ultrathin magnetic nanobelts[J].Phys.Lett.A,2008,372:3857-3860

[15]Y.F.Li,Z.Zhou,S.B.Zhang,and Z.F.Chen,MoS2 Nanoribbons:High Stability and Unusual Electronic andMagnetic Properties[J].J.AM.CHEM.SOC.,2008,130(49):16739-16744

[16]Bin-Zhou Mi,Huai-YuWang,and Yun-Song Zhou, Theoreticalinvestigations of magnetic properties of ferromagnetic singlewalled Nanotubes[J].J.Magn.Magn.Mater.,2010,322(8):952-958

[17]Bin-Zhou Mi,Huai-YuWang,and Yun-Song Zhou, Theoreticalinvestigations of magnetic properties of ferromagnetic single-layered nanobelts[J].Phys.Status Solidi B,1-7(2010)/DO I10.1002/pssb.201046394

[18]P.FröbrichandP.J.Kuntz,Many-body Green’s function theory of Heisenberg films[J].Physics Reports,2006,432:223-304

[19]王怀玉 .凝聚态物理的格林函数理论 [M].北京:科学出版社,2008

[20]王怀玉,夏青,海森伯铁磁系统的总能量[J],物理学报,2007,56(9):5466-05

Spin Waves in FerromagneticM onolayer Nanobelts

M I B inzhou,ZHUANG Yunfei

(Depar tmentOfBasic Curriculum,North China Institute of Science and Technology,Yanjiao Beijing-East 101601)

In this paper,the spin wave spectra of ferromagnetic nanobelts are investigated by means of the the many-body Green’s function method of quantum statistical theory.For a nanobeltwithwidthL,there areLbranchesof energy spectra,ωv=ωv(p),v=1,2,…L.A higher temperature leads to lower energy spectra.The spin-wave energyω(p)dropswith temperature rising,and becomes zero as temperature reachesTC,which is so-called themode softening.At zero temperature,the spin-wave energy is dependent of belt-width,which increaseswithLrising,and approaches that of a 2D monolayer.Comparing the results of spin wave energy spectra of a single-layered nanobeltwith those of a single-walled nanotube,we found that the spectra of the former are non-degenerate.In contrary to that,the spectra of the latter are degenerate.Physically,the degeneracy of the energies is caused by the symmetry.Compared to a nanotube,the symmetry of a nanobelt is reduced significantly.

Ferromagnetic nanobelt;quantized spin models;many-body Green’s function method;spin wave

O 469

A

1672-7169(2011)02-0079-04

2011-03-12

米斌周(1980-),男,甘肃庆阳人,硕士,华北科技学院基础部物理教研室教师,从事大学物理实验教学和磁性纳米材料的计算与模拟工作。