数学分析中分区间方法及应用

孔海涛

(常州信息职业技术学院基础部 江苏常州 213164)

数学分析中分区间方法及应用

孔海涛

(常州信息职业技术学院基础部 江苏常州 213164)

系统地介绍了数学分析中的“分区间法”。结合数学分析教材中关于一致连续、积分的极限、一致收敛等定义以及性质对分区间法的应用进行了系统探讨，得到一些有用的性质和方法。在此基础上，举出一些有代表性的例子，进一步运用所得到的性质和方法，力求使学生在数学分析的学习中加深印象，提高教学效果。

数学分析;分区间法;一致连续

0 引言

在专业数学的数学分析教材中，“分区间法”是很常见的，很多定理的证明以及定积分等定义的引入都充分运用了“分区间法”［1-2］。在数学分析教学中，比较常见的是“分区间法”在一致连续、定积分的定义、积分的极限、一致收敛、实数完备性等方面的应用。在整个数学分析学习体系中，“分区间法”所扮演的角色举足轻重，是数学高等理论学习中独具一格的思想方法［3］。

1 “分区间法”在数学分析中的一些应用

“分区间法”，顾名思义，就是将一段区间分成若干部分，在每一部分上，函数可能具有相同的性质。在专业数学的数学分析教材中，“分区间法”是很常见的，很多定理的证明以及定积分等定义的引入都充分运用了“分区间法”。在本科数学分析教学中，比较常见的是“分区间法”在一致连续、定积分的定义、积分的极限、一致收敛、实数完备性等方面的应用。下文将系统介绍“分区间法”在上述各方面的具体应用。

1.1 “分区间法”与一致连续

直观地说，f在I上一致连续意味着:不论两点x'与x"在其中的什么位置，只要它们的距离小于δ，就可使|f(x')－f(x")|＜ε。当然，根据一致连续定义中δ的出现，正是分区间的关键。如下面的定理1:

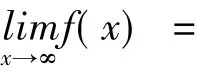
②由Cantor定理，f在［a，Δ+1］上一致连续，故对此ε＞0，∃δ1＞0，当x'，x"∈［a，Δ+1］，|x'－x"|＜δ1时，有

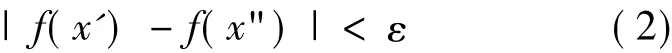
③令δ={1，δ1}，则x'，x"＜a，|x'－x"|＜δ时，x'，x"要么同属于［a，Δ+1］，要么同属于(Δ，∞)。

④从而由(1)、(2)知，只要x'，x"∈［a，∞)，|x'－x"|＜δ，就有|f(x')－f(x")|＜ε，所以f(x)在［a，∞)上一致连续。

从定理1可以初步了解“分区间法”与一致连续问题的关系，例1更深入证明“分区间法”在一致连续相关问题中的应用:

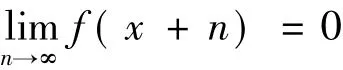
证明:①因f(x)在［0，∞)上一致连续，所以∀ε＞0，∃δ＞0，当|x'－x"|＜δ(x'，x"＞0)时，有

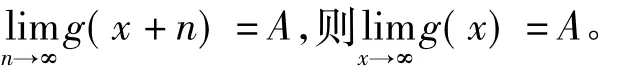
在此，只列出函数一致连续性相关问题与“分区间法”的一些关系。事实上，与此类似的函数项级数一致收敛、含参数积分一致收敛等符合其一致收敛性性质的相关问题均可考虑“分区间法”［3］。

1.2 “分区间法”与积分的极限

当极限的表达式里含有定积分时，把这种极限称为积分的极限。对这种极限，求极限的一般方法理论上都是使用的，所不同的，这里需要充分运用积分的各种特性和运算法则，从而转化为新的定积分［4］。在这些转化过程中，“分区间法”是一种很重要的能简化问题并最终解决问题的方法。

注:此例十分典型，将区间分为两段:其中一段上函数有界，可将区间长度取的任意小，然后固定分点，另一段区间长度有限，函数一致趋于零，因此两段上的积分都任意小。整个积分趋向零。这也是求解积分的极限时候最常用的方法。下面的例3也是这种方法更具体的应用:

例3:设f(x)在［0，1］上连续，则

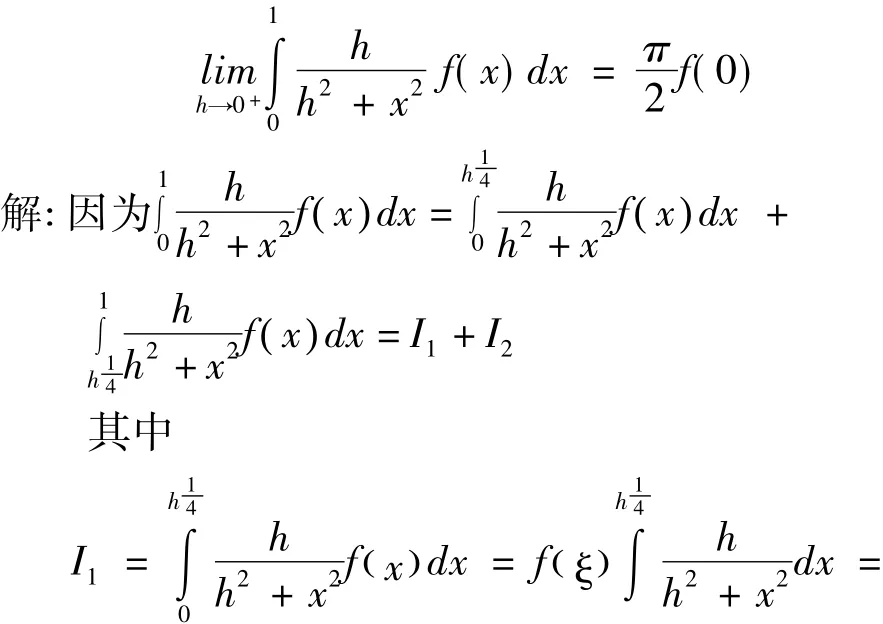
所以上式极限趋向零.在一些情况下，也可以利用“分区间法”将定积分的极限转化为某函数的Darboux的极限，数学分析中著名的Riemann引理的证明［5］正是运用这样的思想。

2 结束语

本文主要介绍了“分区间法”在数学分析中某些方面的应用，当然“分区间法”在数学分析中的应用还远远不止这些，但其在一致连续、定积分的定义、积分的极限、一致收敛、实数完备性方面的应用是非常典型的，上述所给出的每一个例子都具有代表性，能明确地表达“分区间法”的意义。

［1］ 华东师范大学数学系.数学分析［M］.北京:高等教育出版社，1997:53-54.

［2］ 裴礼文.数学分析中的典型问题与方法［M］.北京:高等教育出版社，1993:67-68.

［3］ 唐美艳.证明函数一致连续的几种方法［J］.贵州师范学院学报，2010，26(12):7-10.

［4］ 孙秀华，吕诚.探讨积分的极限［J］.合肥师范学院学报，2007，17(4):70-72.

［5］ 钱吉林.数学分析题解精粹［M］.武汉:崇文书局，2009:73-74.

Dividing Method and Its Application in Mathematical Analysis

KONG Hai-tao
(Department of Basic Courses，Changzhou College of Information Technology，Changzhou 213164，China)

The paper mainly introduces the dividing method in mathematical analysis.By analyzing the uniform continuity，the definition of the definite integration，the limit of integration，and uniform convergence we explore the application of the dividing method radically and get some useful conclusions.Based on that，we give some typical examples to illustrate the properties and methods we have got.The purpose of this paper is to improve our teaching effect and make the students learn the course well.

mathematical analysis;dividing method;uniform continuity

O 17

A

1672-2434(2011)03-0047-03

2010-12-28

孔海涛(1980-)，男，讲师，从事研究方向:数学教育