同步气象卫星视地理坐标与像素直角坐标的转换关系及误差分析

2011-12-23董明伦周炯

海洋预报 2011年2期

关键词：气象卫星纬度垂线

董明伦，周炯

（中国卫星海上测控部，江苏江阴 214431）

同步气象卫星视地理坐标与像素直角坐标的转换关系及误差分析

董明伦，周炯

（中国卫星海上测控部，江苏江阴 214431）

利用WGS-84坐标系模型及纬度的定义办法，根据同步气象卫星的视成像原理，导出了同步气象卫星云图像素的视地理坐标与直角坐标的转换关系，建立起一种像素地理坐标定位的理论模型，并对模型进行了误差分析，用实收云图验证表明，推理正确，结论可靠，为同步气象卫星数字化云图资料的再定位和下游延伸研究和应用提供了一种可靠的定位方法。

视地理坐标；气象卫星；转换；误差；定位

1 引言

视地理坐标投影图虽然不是标准的地图投影图，但是随着卫星遥感图像的广泛使用，视地理坐标投影图在科研和实践中被广泛应用。在同步卫星遥感“成像”过程中，卫星是把“看到”的三维地理坐标物像形成二维平面直角坐标物像，而不是把地理坐标转换成平面直角坐标，人们在使用时需要把二维平面直角坐标转换成三维地理坐标。如FY-2C、FY-2D、MTSAT等同步气象卫星，在扫描完近似半球的表层大气层后，需要在平面上形成两维的卫星云图或水汽图等。一般情况下，卫星下发的是成品图像，也有的气象卫星下发扫描的原始数据。但不管怎样，气象人员都需要在二维的云图上面解读出三维地理坐标的经纬度，以方便使用。例如，在红外云图上标注台风的位置，或者在研究工作中需要数字化处理二维云图上的经纬度等等，都需要把卫星形成在二维平面的视经纬坐标转换成平面直角坐标，或者把平面二维直角坐标转换成平面视地理坐标系的经纬度，以方便研究和数字化处理。但是由于地球不是气象领域传统理论所依据的圆球体，而卫星成像所依据的是近似椭球体，故两者在对同一地点定位时会产生较大的差异，这种误差在精确定位或数字化处理图像时是无法接受的。

另外，在气象科研和业务中，经常在卫星云图上定位和读取地理坐标值。一方面较低的分辨率和较小的图像使得定位精度很低。另一方面成像规律决定了离图像中心点越远，误差越大。所以在局部定位时，应当精确到像素点，否则也会产生较大的定位误差，进而影响预报精度或研究精度。

本文以WGS-84坐标系为模型，对上述问题进行了研究和探讨，导出了一种转换模型，经过MTSAT气象卫星云图上验证，证明精度可靠，行之有效。

2 理论依据

本文理论推导及误差分析所用到的主要概念是纬度的定义和WGS-84坐标系。

2.1 常用纬度的分类和定义[1]

纬度的定义：纬度是指地球上某点的垂线方向与赤道平面的夹角。根据垂线的不同种类有多种纬度定义。常用的定义有以下4种：

地心垂线与地心纬度：从地球表面某点到地心之间的连线为地心垂线。它与赤道平面的夹角就是地心纬度。

引力垂线和引力纬度：地球表面某点的质量与所受地球引力方向线叫引力垂线。它与赤道平面的夹角就是引力纬度。引力垂线一般不经过地心，但差别较小，一般不用它。它可能对卫星的定位有影响。

地理垂线和地理纬度：地球表面某点的法线方向线叫地理垂线，也叫测地垂线。它与赤道平面的夹角就是地理纬度，也叫测地纬度。

重力垂线和重力纬度：地球表面某点实际重力作用的方向线叫重力垂线，它与该点的水准面垂直。它与赤道平面的夹角就是重力纬度。因为受到天文因素的影响，也可以用天文方法测出该纬度，因此也叫天文纬度。天文纬度与地理纬度的差别也不大。

虽然纬度的定义有多种，但是它们是针对不同的用途和研究问题的方便而定义的，而它们之间也确实存在差异。在大地测量、地图绘制、精确导航和定位中，都使用地理纬度。本文使用的纬度也是地理纬度。

2.2WGS-84坐标系

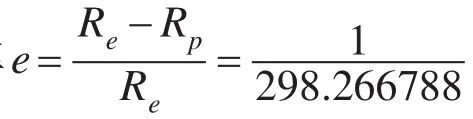
2.3 子午圈直角坐标与纬度的对应关系

在子午圈平面直角坐标系中，原点是地心，而非地理中心，横坐标在赤道的法线方向，纵坐标是极轴，指向正北，按照WGS-84坐标系模型的规定，子午圈平面都是椭圆平面。根据椭圆方程的定义，可导出地球表面任意点C（x,y）的直角坐标与纬度Φ的关系（图略）。

上述二式就是WGS-84坐标系中子午面上地表任意一点的直角坐标与纬度的对应关系，当然它们适用于任意子午线。

3 像素的视地理坐标系转换

太空探测器所探测的三维地表地理位置就是由上述子午线坐标点所组成的集合，并把探测到的三维地表坐标转换成二维平面直角坐标或者转换成二维平面上的地理坐标，以获得各种比例（分辨率）的探测图像。就地球同步气象卫星而言，轨道在天球赤道上，轨道周期与地球同步，所以它探测的地球表面是固定的区域，所获得的图像就是该区域某分辨率的云图，云图上所标识的像素直角坐标就是卫星所“看到”的子午线坐标集合，本文用 px和 py表示（见图1）。而将像素的直角坐标所对应的地理坐标称为“视地理坐标”。

从图1不难看出，“视地理坐标”是三维球面坐标经点射线源投影后，在平面上形成的二维坐标。

3.1 同步气象卫星成图原理

同步气象卫星是按“数字化”方式扫描大气层的，就是根据最低分辨率把能够识别的地表最小面积形成一个最小识别单位，这就是一个像素点，把连续扫描的全部面积单位排列成一条像素数据链，再按固定行列宽“折迭”成一张完整的图像，这就是我们常见的数字化卫星云图。例如MTSAT卫星所播发的IR云图就是如此。

3.2 视地理坐标与像素直角坐标变换原理

图2是一维视地理坐标成像原理。半视宽AD（常数），在视距OA（常数）增加AB后，在AD上的像为AE。不难看出，AE与AB的对应关系是：

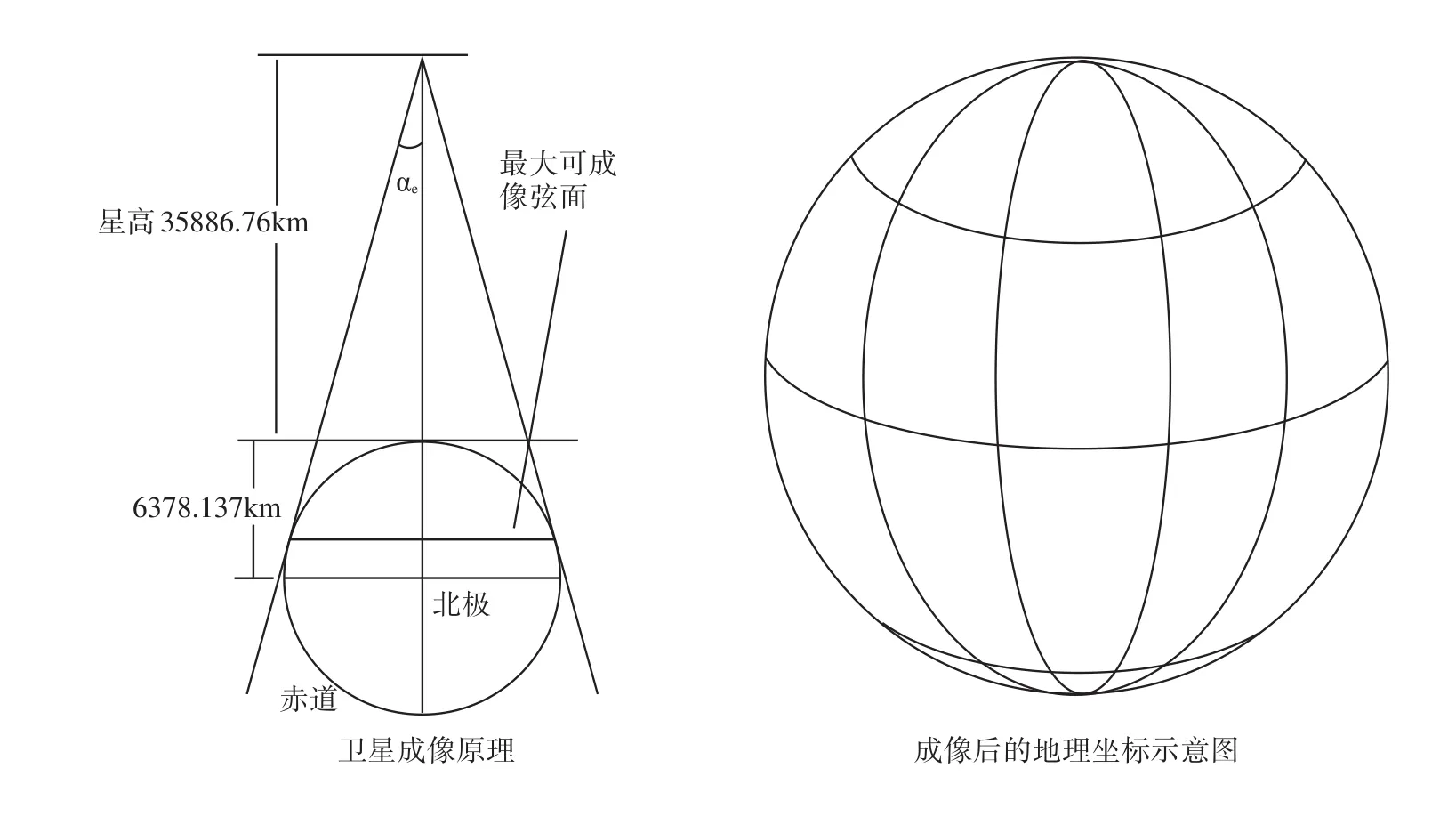
图1 同步气象卫星的成像原理和地理视坐标原理

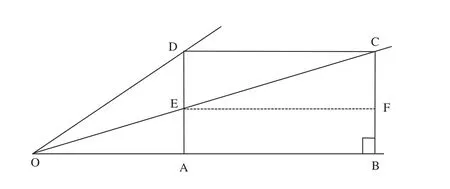
图2 视觉成像原理

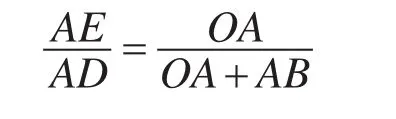
对三维地球表面上任意点C，见图3，P是同步气象卫星，A是星下点。

图中OA=Re，OC=R,则三维球面坐标的成像原理见图4。

图4中，直角坐标系的原点是星下点A，横坐标指向正东，纵坐标指向正北且平行于极轴。平面 pxApy是成像面，子午线上任意一点C(x,y)的像是D(px,py)，在WGS-84坐标系中，C(x,y)的坐标值由（1）和（2）式给出。根据几何相似原理，并考虑到图3中C(x,y)坐标在赤道平面和星下点子午面上的投影，不难得到下面的几何相似比例关系：

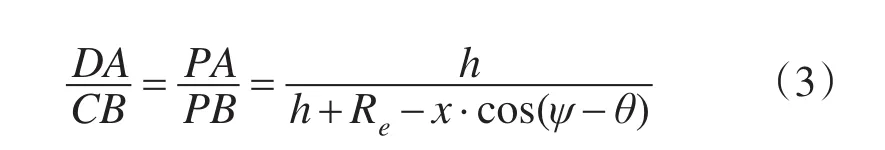
式中θ是星下点的经度，Ψ是C点子午线经度，星高h=PA。

在图3和图4中，根据几何相似比例关系：

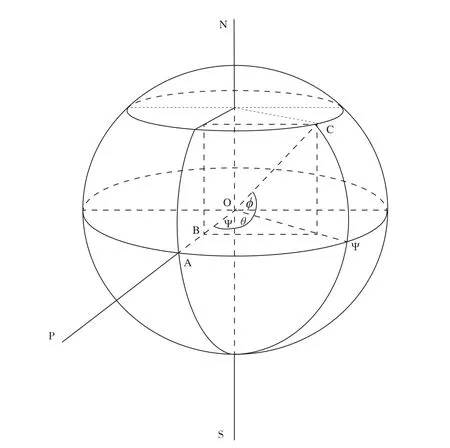
图3 同步气象卫星成像原理

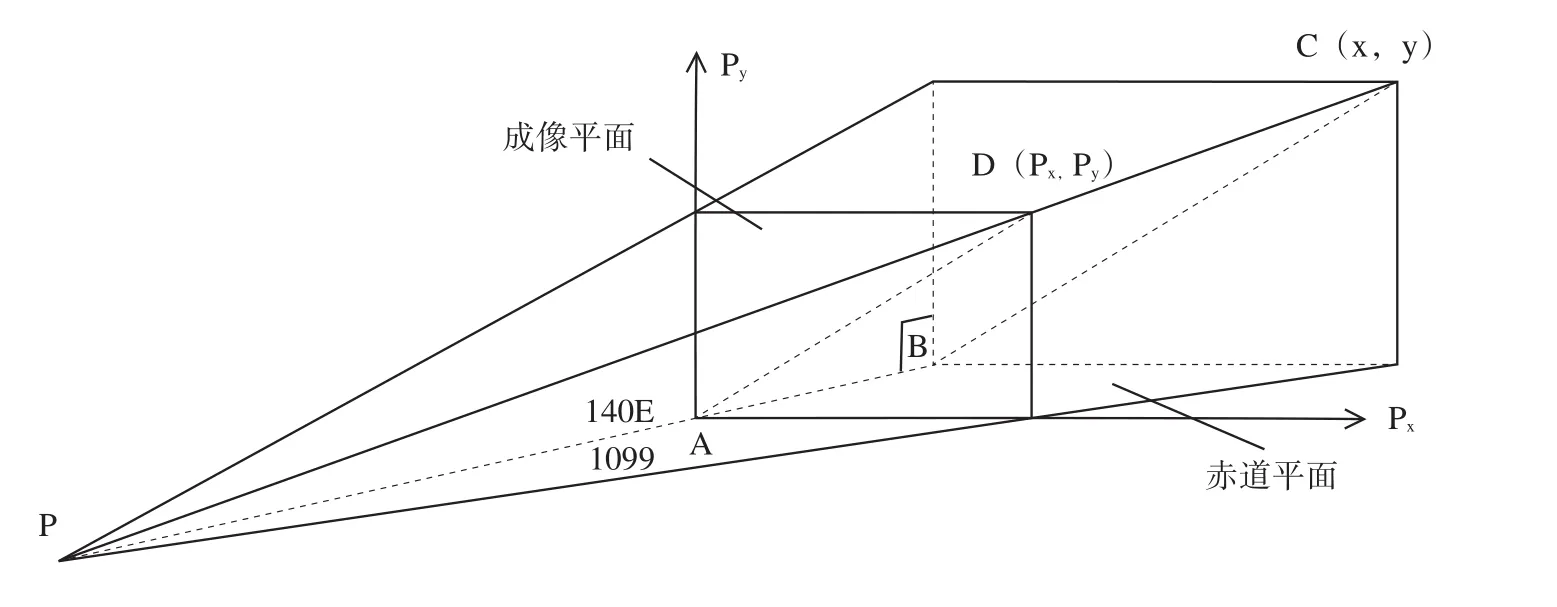
图4 子午线任意点C（x,y）的视坐标成像原理

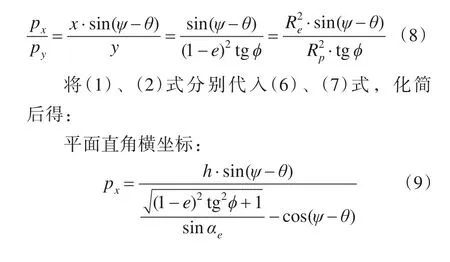
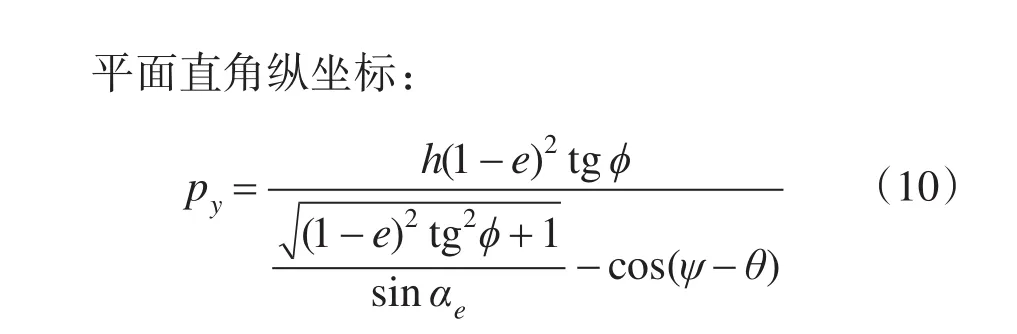
这就是视地理坐标与像素平面直角坐标的转换关系。当 θ＜ψ＜180°或 ψ＞180°（西经）时，px≥0，否则， px＜0。对于 py，北纬时 py≥0，南纬时 py＜0。

（9）、（10）式等号右边除经纬度参数外，其余都是常量，说明，在WGS-84坐标系下，同步气象卫星云图的像素直角坐标仅与地理坐标有关，与子午圈的半径无关。需要特别说明的是，px和py的原点在云图的几何中心，也就是像素链的中间点。用计算机处理云图数据时，应把原点平移到图像的左上角，即像素数据链的起点即可，可用加减法运算实现，不再赘述。这样按照（9）、（10）式，只要知道地理坐标，就可以确定该点在像素数据链中的位置，反之，也可以根据像素在像素数据链中的位置，给出其精确地理坐标，实现不必成图就可对各像素“定位”的目的，这给计算机根据云图自动跟踪局地云的变化，或从指定区域提取云的信息提供了极大的方便。

在卫星云图上，px和 py是无量纲的像素点的坐标值，据此（9）、（10）式中，卫星高度h、赤道半径Re的单位用无量纲的像素数表示，其值由后面的“实验验证”给出。

3.3 像素平面直角坐标与视地理坐标的转换关系

根据（8）、（9）、（10）式，可导出平面直角坐标与视地理坐标的转换关系。消去tgφ，化简后令：

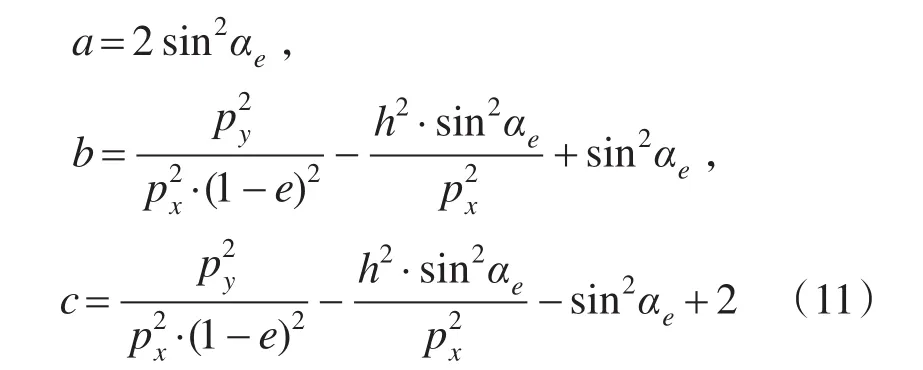
式中αe是同步卫星扫描地球时东西向的最大可视半角，见图1。

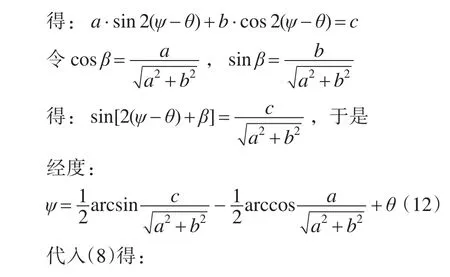
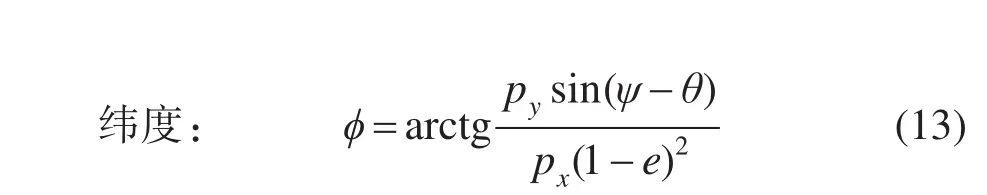
（12）式和（13）式就是图像平面直角坐标转换为视地理坐标的关系式，等号右边a、b、c由（11）式给出，在（11）式中， px和 py是像素坐标值，其余都是常数。

4 误差分析

理论和实践表明，在WGS-84坐标系模型中，经度的理论值与实际误差很小，实际应用中可以忽略不计；但纬度误差比较大，成因也比较复杂。一方面地球是非均质球体，其质心受各种因素的影响，在不停地变化着；另一方面地球形状与WGS-84坐标系模型也有差异，主要体现在北极高出参考椭球约10 km，而南极要低于参考椭球约30 km[1]，幸运地是，气象同步卫星的探测范围只能覆盖南北纬80°以内的区域，因而极区的差异对云图上的定位影响不大，可以忽略。纬度的定位误差主要体现在以下几个方面：

4.1 纬度的垂线偏差[1]

垂线偏差是地心纬度与地理纬度的差异引起的。由于地球中心和地理中心不重合，使地心纬度ϕc和地理纬度Φ之间存在一个偏差Δϕ，这就是垂线偏差。

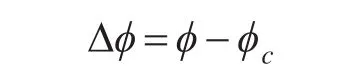
设以地心为原点的参考椭球上M点的坐标为M(xc,yc)见图5。则椭圆方程为：

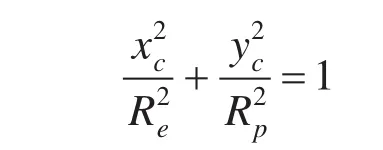
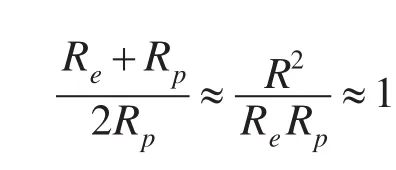
地理纬度与地心纬度之间的偏差：

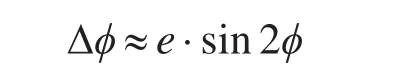
显然，ϕ=45°时，垂线偏差最大，约11分，在子午线上产生大约20 km的偏差。即在南北纬45°的两个纬圈上，地心纬度与地理纬度相差最大，对精确定位有很大影响。

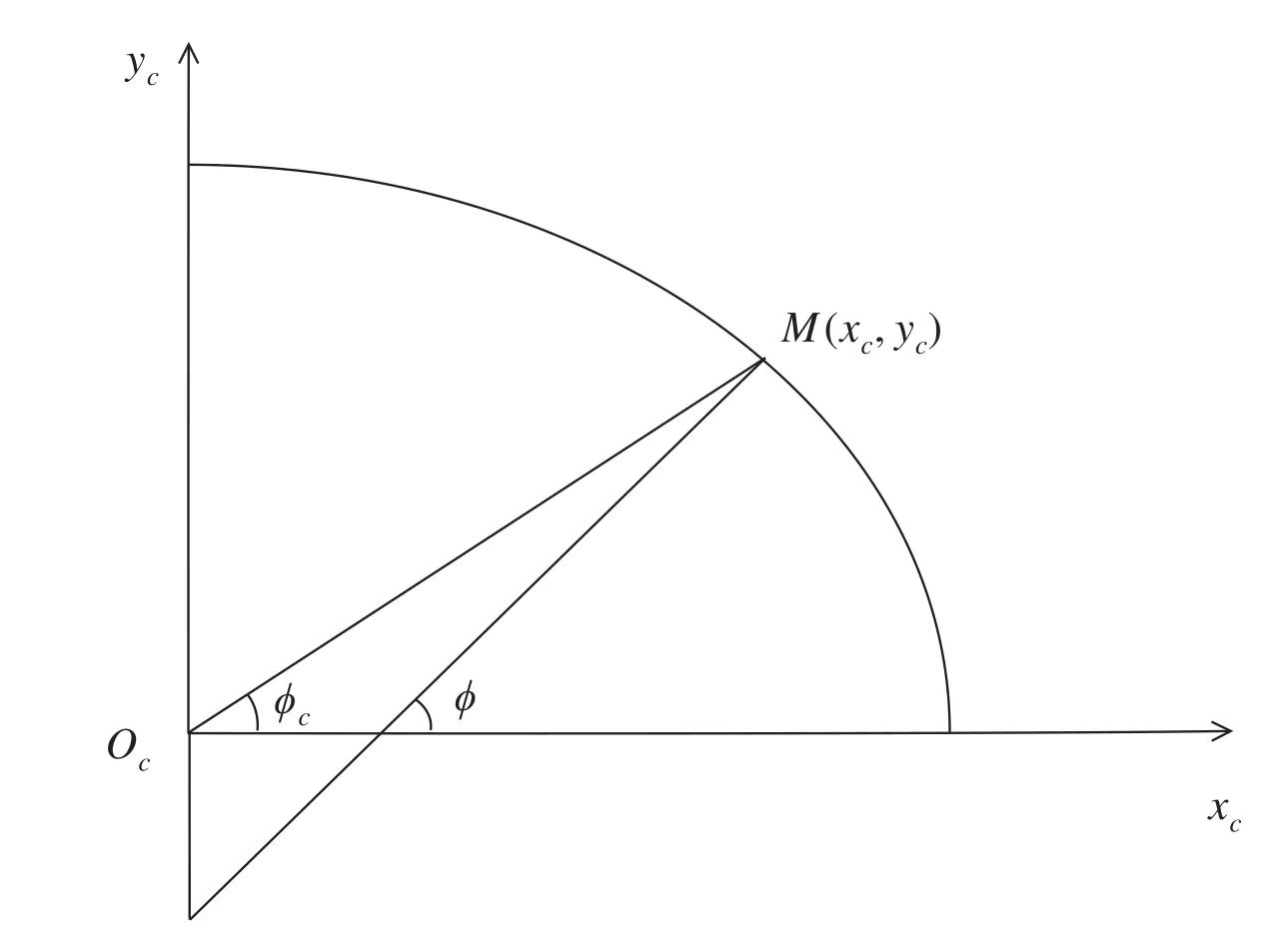
图5 垂线偏差

4.2 垂线偏差对同步卫星IR云图的定位影响

因为IR卫星云图像素的最大分辨率约5 km，故11分的纬度偏差约合4个像素。即南北方向定位时最大产生4个像素的偏差。该偏差对云图的定性使用影响不大，但对计算机处理卫星云图数据有较大影响，是不能忽略的。

4.3 高云的非星下点误差影响

（9）和（10）式的推算过程中，没有考虑云高对定位的影响，即假定云高为零。该假定会使云图上离星下点越远的像素定位误差越大，尤其是IR云图边缘上的低纬区域的强对流云，由于对流层顶在10 km以上，会使云图横向“扩展”开来，使定位被压缩约2个像素点。解决办法是适当增加Re的数值。但这种做法意义不大，因为就实用性而言，同步气象卫星云图边缘区域云的信息和地理信息叠加严重，基本没有使用价值；云高产生的误差对台风的精确定位有较大影响，经向和纬向都有误差，一般各产生1个像素点的差异，即各5 km左右。

4.4 视地理坐标误差分布特点

由图1不难看出，从星下点开始沿半径方向的地理坐标信息密度越来越大，增加很快，接近边缘处出现“叠加效应”，即同一个像素对应多个不同的经纬度组合，使定位产生不确定性。即由图像中心到边缘区域，像素的定位误差越来越大，这就是视地理坐标误差分布特点。

5 实验验证

以MTSAT的IR通道云图为例，该星位于东经140°赤道上空，有多种探测通道。为计算方便，选取离边缘近的点，这样做的另一个好处是如果计算得到的误差较小，就更能证明模型的可靠性。为此取点（170°E，60°N）。

实测MTSAT的IR通道云图一张完整的卫星云图由2200×2200像素组成。星下点坐标是（1100，1099），原点在左上角。

设αe是卫星扫描地球时东西向最大可视半角，同步气象卫星对地理论高度h=35886.76km，则是：

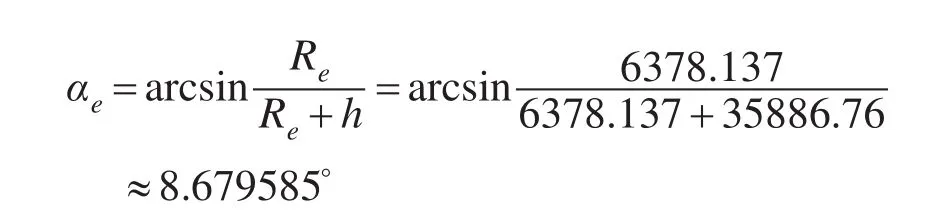
实测在2200×2200投影面坐标系中，卫星扫描地球时东西向的最大弦半径（见图1）

re=1085 pix，故星高：

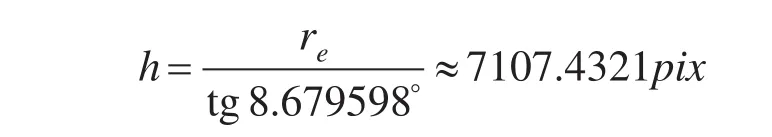
代人（9）、（10）式整理得：

横坐标：

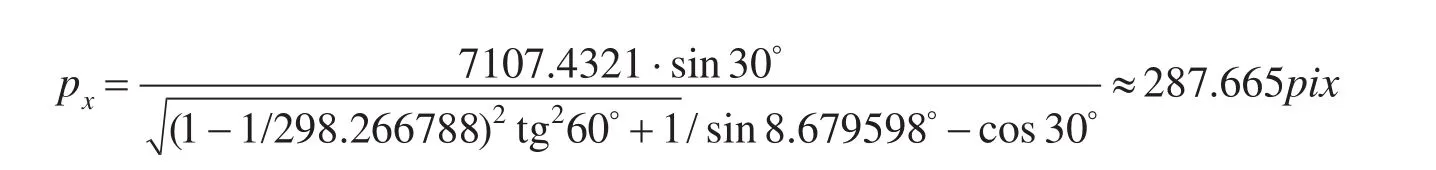
与实测比较：在IR云图上（170°E，60°N）的平面直角坐标是（288，994）。东西向相差0.3个像素符合实际；南北向相差4.6个像素，偏差较大。产生经向误差小纬向误差大的主要原因有三个方面：一是WGS-84坐标系模型与现实地球之间存在的差异，高纬度地区北半球的纬圈半径比同纬度WGS-84坐标系模型大，而南半球则偏小[1]。这样一方面使实际子午线上北纬坐标比WGS-84坐标系模型坐标小，南纬坐标偏大，另一方面北半球中纬度地区地理坐标的高程始终大于模型坐标的高程；使得北半球该误差始终为正；二是现实地理坐标系与地心坐标系之间存在差异，就是垂线差： Δϕ≈e·sin2ϕ=esin120°≈2pix ，北半球垂线差的特点也是始终为正；三是测量原因，属随机误差，特点是越靠近图像边缘，单位像素的测量误差越大。测量误差的另一个特点是可正可负。本测量点已靠近图像边缘区域，因此测量误差较大。

综上，不考虑测量误差时，则在4.6个pix的误差中，用模型和垂线差可修去3～4个pix，余下的0.6～1.6个pix属测量误差和地理信息叠加产生的误差之和，基本不可修正。这样修正后南北向的偏差也属可控范围。

由像素的平面直角坐标反向推算地理坐标的实验（略）。