两种网格下的SWAN模式对黄渤海海浪模拟比较
2011-12-23史剑王璞钟中张军
史剑,王璞,2,钟中,张军
(1.解放军理工大学气象学院,江苏南京211101;2.72517部队,山东济南 250022)
两种网格下的SWAN模式对黄渤海海浪模拟比较
史剑1,王璞1,2,钟中1,张军1
(1.解放军理工大学气象学院,江苏南京211101;2.72517部队,山东济南 250022)
采用NCEP再分析风场作为驱动海浪模式的强迫场,在考虑相同物理过程和分辨率基础上,SWAN海浪模式分别采用矩形网格和非结构三角网格对2000年12月黄渤海海域波浪场进行模拟,并将模拟的有效波高与海洋浮标观测数据作对比分析,结果表明,SWAN模式运用两种网格均能够取得良好的模拟结果,相对矩形网格,非结构三角网格模拟有效波高效果较好,且能够较好的刻画复杂地形。最后,采用局部加密的非结构三角网格对黄渤海波浪场进行模拟验证,分析表明非结构三角网格的局部加密方案可以进一步提高加密区域的有效波高模拟精度。
SWAN海浪模式;非结构网格;有效波高
1 引言
海浪在海-气相互作用研究中占有非常重要的地位,它是参与大气底边界层和上层海洋之间物质、动量和热量交换的一个重要过程[1-2]。海浪的数值模式已被广泛用于模拟海浪生成、传播和发展规律,而且还是海浪预报的主要手段和工具。目前,比较成熟的海浪数值模式有第三代海浪模式 SWAN(Simulating Waves Nearshore)、WAVEWATCH等。其中SWAN发展到今天,已具有稳定性好、计算精度较高等特点,且被广泛应用于河口、海岸和近海海域的海浪数值模拟。蒋小平等[3]应用SWAN模式对Winnie(1997)引起的台风浪进行模拟,将模拟的有效波高与TOPEX/POSEIDON和ERS-2卫星高度计资料作对比分析,并分析了台风浪要素的分布特征,结果表明SWAN在模拟较大尺度的海区时能得到较好模拟效果。杨德周等[4]将SWAN模式应用到渤海,发现SWAN中的Phillips线性增长部分的比例系数随摩擦速度变化,引入了新的Phillips线性增长项公式,通过与实测数据验证,表明改进后的Phillips线性增长项更适用于渤海。梅婵娟等[5]分别利用SWAN和WAVEWATCH模式对黄海区域进行了理想情况和实际浪场的模拟计算,结果显示,理想状态下两模式模拟结果在大小和空间分布上都不相同,但在大小及变化趋势上相差不大,实际模拟中,SWAN模式模拟结果较WAVEWATCH模式好。胡克林等[6]利用曲线网格下的SWAN模式模拟长江口附近海域台风浪,通过浮标实测资料验证,显示有效波高模拟值与实测值符合良好,综合分析模拟的波浪场表明SWAN模式能合理反映长江口附近海域台风浪分布。
目前,多采用嵌套技术获得较高分辨率网格以达到提高数值模式模拟和预报精度的目的。SWAN40.81版本模式将采纳非结构网格计算。为我们提供了另一种提高模拟精度的途径。黄必桂[7]采用矩形网格的自嵌套方案和非结构三角网格局部加密方案对渤海海浪进行模拟,发现使用非结构三角网格同样可以达到自嵌套矩形网格模拟的精度。Jianhua Qi等[8]将非结构三角网格下的SWAN模式应用于美国缅因海湾表面波浪模拟,表明非结构网格可以改进网格对复杂的不规则海岸地形的空间匹配,采用非结构网格的SWAN模式能够较好的反映美国东北部近海表面波浪的空间和时间变化。本文将采用非结构网格和矩形网格的SWAN模式应用于黄渤海海域,比较不同网格下模式对中国黄渤海浪高的模拟能力。
2 海浪模式简介
本文采用海浪模式SWAN的最新版本40.81对黄渤海海浪进行模拟。SWAN模式采用波作用量密度谱 N(σ,θ),而不是能量密度谱 E(σ,θ)作为控制变量。这是因为在环境流场存在的情况下,波流相互作用使得能量密度谱不再守恒,但波作用量密度谱却是守恒量[9-10]。在直角坐标系下,波作用量平衡方程描述为:

等式右边的Stot是源汇项,其中Stot包括风能输入项、白冠耗散项、深度诱导破碎项、底摩擦耗散项、三波和四波波-波非线性相互作用项。
SWAN40.81版本提供了另一种网格形式——非结构三角网格,这种网格使用起来灵活性、适应性强,尤其适合应用于水深变化急剧和岸线复杂的近岸、近海区域。

图1 22101浮标实测风矢量与NCEP再分析风场插值到浮标坐标处的风矢量比较图
3 两种网格下的黄渤海海浪数值模拟
3.1 数据资料
本文SWAN模式计算的输入风场来自购买的NCEP再分析风场数据。该数据提供的风场时间分辨率为3 h,空间分辨率为0.25°×0.25°。本文输入风场的时间段为2000年11月30日09时—12月31日23时,风场数据范围为115°—150°E,20°—50°N,完全覆盖了整个黄渤海海域。
本文将NCEP再分析风场数据插值到浮标22101所在位置(126.01°E,37.14°N)的风矢量与浮标实测矢量相比较(见图1),可以看出,时-空插值后的风矢量与实测风矢量大致符合。另外做了22101浮标实测风速与NCEP再分析风场插值到浮标坐标处的风速随时间变化图(见图2),整体而言,NCEP再分析风场可以较好的描述所取时间过程的风速变化趋势。可以说,NCEP再分析风场作为输入风场精度比较高,为海浪的数值模拟准备了良好的前提条件。
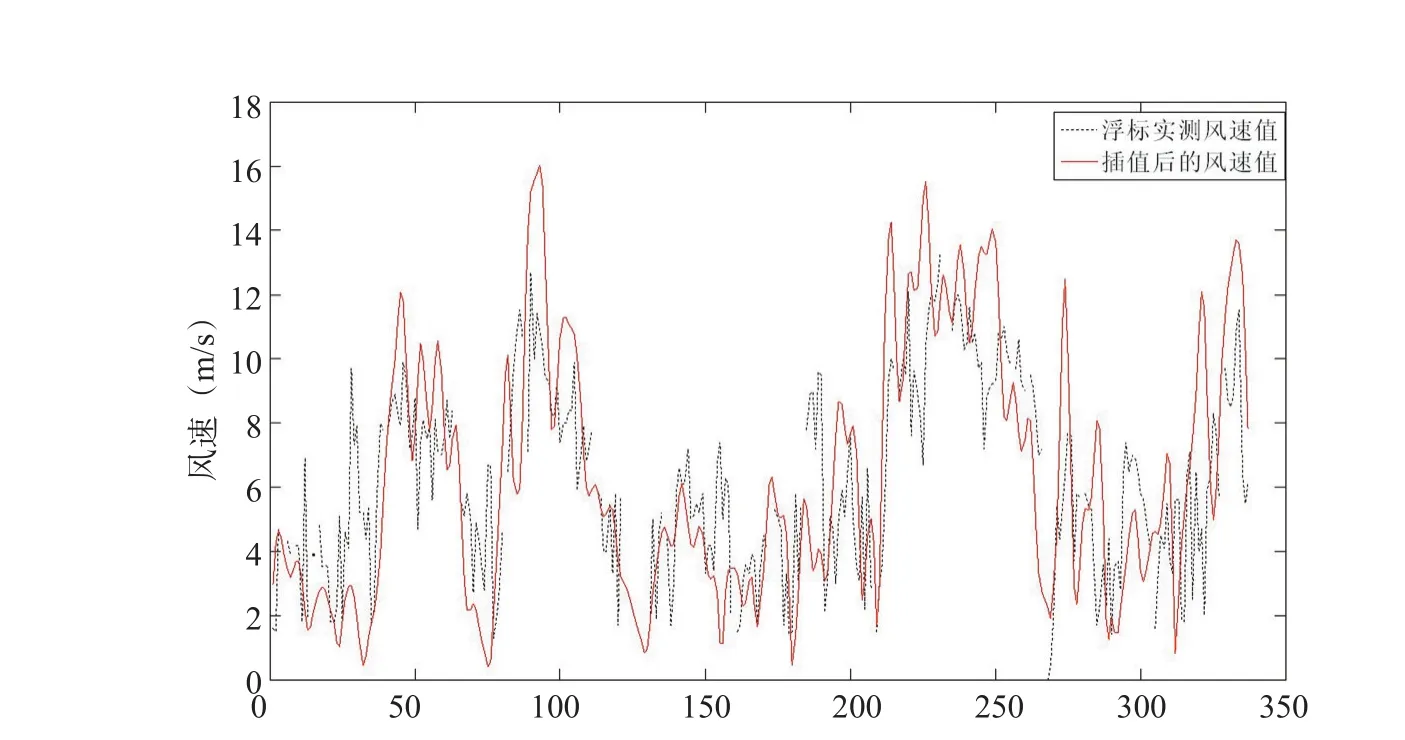
图2 22101浮标实测风速与NCEP再分析风场插值到浮标坐标处的风速比较图
渤海为半封闭海湾,仅通过渤海海峡与黄海相通,黄海又与西北太平洋相通。黄渤海海域岸线崎岖,岛屿众多,地形、地貌较为多样。本文使用的海岸线数据是美国国家地球物理资料中心NGDC(National Geophysical Data Center)提供的全球分级高分辨率岸线数据GSHHS(Global Self-consistent Hierarchical High-resolution Shorelines)。选用GSHHS中等级分辨率数据(Intermediate resolution data)进行提取。水深数据是从NGDC提供的全球陆地海洋DEM高程数据ETOPO5中提取,空间网格分辨率为5'×5'。其水深分布见图3。由图可知,黄渤海海域大部分区域水深小于100 m,渤海海域大部分区域水深小于50 m。整个海域水深由陆地边界向中央逐渐变深,其中山东、江苏沿海等值线分布较疏,水深梯度较小;朝鲜半岛南侧、西侧沿海等值线分布较密,水深梯度较大。第一岛链附近水深梯度很大。
文中用于验证的实测资料来自2000年12月的两个海洋浮标资料,分别为22101(126.01°E,37.14°N)和22102(125.46°E,34.48°N),见图3—4。
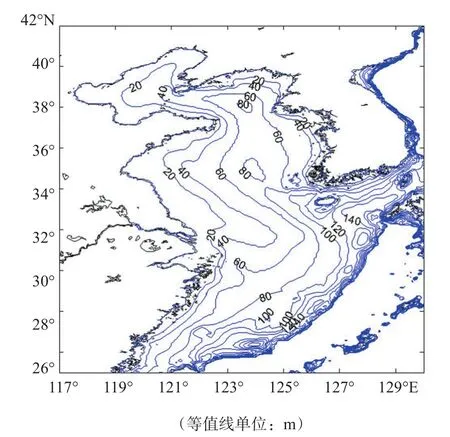
图3 计算区域水深等值线分布图

3.2SWAN模式的设置
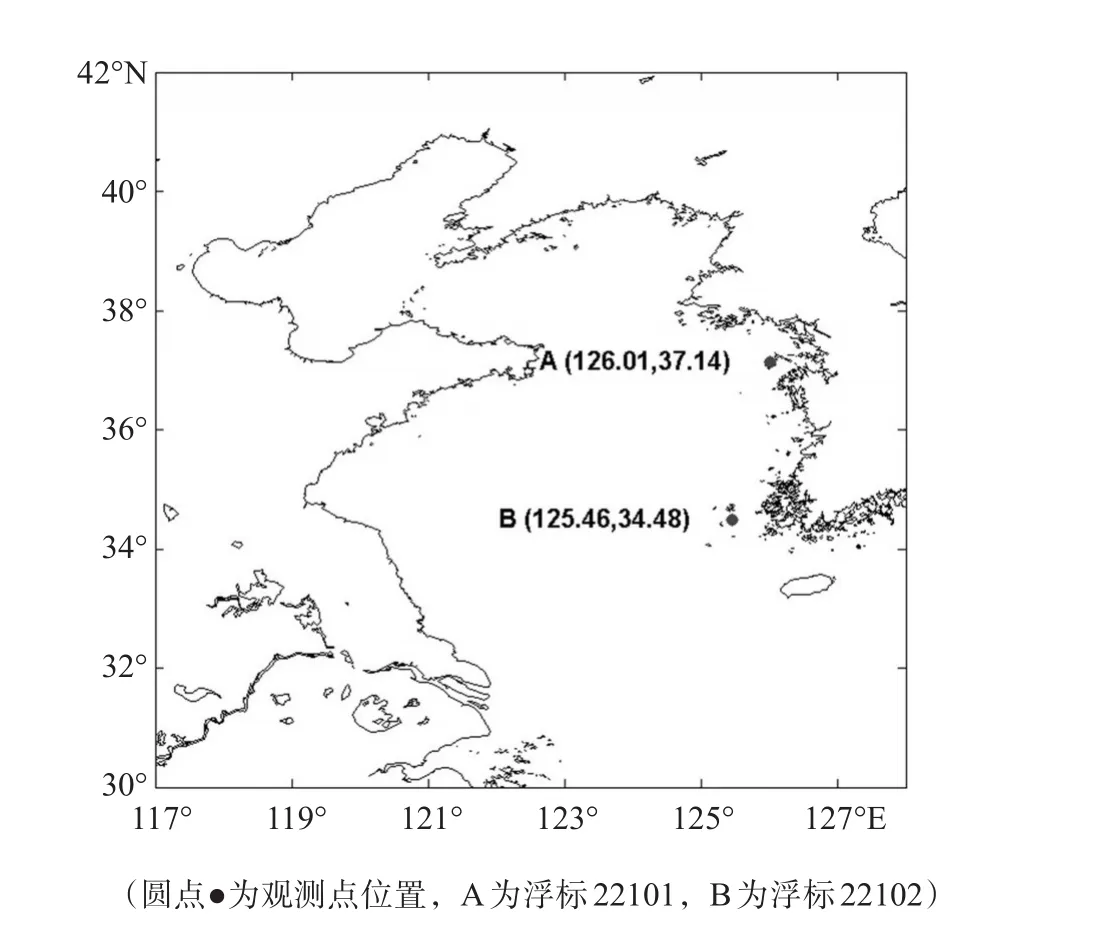
图4 观测点位置

图5 非结构三角网格(图中蓝色弧线为开边界)
对于开边界,波浪可以自由出入,开边界上的能谱边界条件是模拟时考虑的要素之一。尽管在本次实验所取的开边界上无法获取入射波的观测数据,但在12月份的黄渤海区域,西北风盛行并占有优势,从陆地吹向海洋,如果开边界取的离模式输出点足够远,边界上的波作用对模拟的影响很小。本文在模式计算中假定开边界没有波传入计算区域。
实验的模拟时间从11月30日09时—12月15日00时,时间步长为1 h。模式初始化方法采用基于初始输入有限风场的JONSWAP谱,采用球坐标系下的非静态模式。为了减小初始状态对输出结果的影响,本文模式输出从12月1日00时开始,输出时间间隔为1 h,方向间隔取为10°,即36个方向,频率范围为0.05—1Hz。葛义军等[11]认为对于谱空间离散方案,不论取何种频率范围,模拟误差基本上随着方向间隔增大而增大,取较小的方向间隔可以有效提高模拟精度。
3.3 模拟结果与实测资料的对比分析
为定量对数值模拟结果和观测资料进行对比分析,本文采用了相关系数Cor、均方根误差RMSE、平均绝对误差MAE三个统计量,定义分别如下:


xi代表观测值, yi代表模拟值,、分别代表观测值和模拟值的平均值,N代表样本总数。
在网格分辨率相同情况下,相同的机器配置,采用矩形网格计算用时1小时11分钟,采用非结构三角网格计算用时2小时21分钟,可见非结构三角网格单机运算效率较低。图3-6是两种网格下的模式输出有效波高分别与浮标资料的散布图,由图可知,大多数点都在对角线附近,这表明两种网格的计算结果与实测值均具有较好的相关性。图6(a)、(b)散点分布较相近,但在某些波高实测值,比如0.5 m、0.7 m、1.5 m等处,图6(b)比图3-6(a)更靠近对角线,说明非结构三角网格的模拟结果较矩形网格有向好趋势。图3-6(c)、(d)则不显著。由图还可看出,浮标22102处,两种网格在1 m以内小波高处的模拟值与实测值更为接近,而当波高大于1 m,模拟值大部分小于实测值,总体上大部分点在对角线以下,表明浮标22102处模拟值较实测值有低估趋势。浮标22101处两种网格下模式模拟结果位于对角线以上的点较多,表明模拟值较实测值有高估趋势。表1和表2给出了相关系数、均方根误差和平均绝对误差3种统计量。其中,非结构三角网格计算结果与实测值的相关系数较矩形网格略有提高。此外,从误差分析结果来看,非结构三角网格计算结果的均方根误差、平均绝对误差较矩形网格也都略有减小。综合以上分析表明使用非结构三角网格后,SWAN模式的模拟能力有所提升。

表1 两种网格模拟的有效波高结果与浮标22101实测值的相关系数、均方根误差、平均绝对误差

表2 两种网格模拟的有效波高结果与浮标22102实测值的相关系数、均方根误差、平均绝对误差

图6 矩形网格、非结构三角网格模拟结果与浮标实测值的散布图
图7分别给出了两个浮标测站两种网格下模式模拟的有效波高值和实测值随时间变化对比图。时间跨度从12月1日00时—12月15日00时共337个小时,模式每一小时输出一个有效波高值。从两个浮标测站的对比图可以看出,两种网格下的模式模拟结果与实测值均有良好的吻合,都能很好的体现出实际浪高的变化趋势。整体上,当有效波高在1 m附近或大于1 m时,模拟值普遍低于实测值;而当有效波高小于0.5 m时,模拟值高于实测值。在波浪发展到第270小时至最后,有效波高大于1 m时的模拟值比实测值偏大,这在浮标22101处体现的更明显。从两种网格模拟结果的对比分析来看,大多数时刻的模拟结果比较接近,但仍有一些差异。图7a中,在第70—120小时的波高增长过程中,矩形网格模拟值增长较快,导致模拟值高于实测值。非结构三角网格增长相对滞后于矩形网格而更趋近实测值。在波高衰减阶段,矩形网格模拟的波高衰减也比非结构三角网格稍快,从而低于实测值,而非结构三角网格更接近实测值。在随后的第200—250小时、第270—300小时、第300小时至最后的波高变化过程中,当矩形网格模拟值低于实测值时,非结构三角网格模拟值则高出矩形网格更接近实测值;当矩形网格模拟值高出实测值时,非结构三角网格模拟值则低于矩形网格更接近实测值。这说明非结构三角网格较矩形网格更能使模拟结果有向好趋势。图7b中虽表现的不明显,但依然有此趋势。综上所述,当网格分辨率达到一定程度(此处取5'×5'),各物理过程考虑一致的情况下,两种网格下的模式模拟结果比较接近,但计算网格的选取仍可一定程度影响到模拟结果的精度。采用非结构三角网格计算可以使模式模拟能力得到提升。

图7 矩形网格、非结构三角网格模拟结果与浮标有效波高实测值随时间变化对比图
图8为两种网格下模式模拟的黄渤海海域12月15日00时有效波高分布图。由图不难看出,两种网格下模式模拟的黄渤海浪高分布情况比较一致,两结果几乎有着相同的浪高大值中心区域。在124°—125°E,38°—39°N这个海域,两结果略有差异,非结构三角网格的浪高大值区域范围较矩形网格有所缩小。相对矩形网格,非结构三角网格对地形的刻画具有一定优势,比如,非结构三角网格的海岸线边界与实际拟合较好,随着海岸线边界上节点密度加大会更符合真实情况;矩形网格的海岸线边界多呈锯齿状,存在失真(见图9)。从图9(d)可看出,非结构三角网格对近岸岛屿刻画较清晰;而矩形网格则无法表现。
4 非结构三角网格局部加密方案
由前文可知,在相同的网格分辨率下,计算网格的选取对模拟结果是有影响的。矩形网格和非结构三角网格在关注区域均能达到良好的模拟效果,相比而言,非结构三角网格的整体模拟效果较优于矩形网格。非结构三角网格的另一优势是可以对关注区域方便地进行局部加密,而不用通过模式嵌套来实现。下文即采用非结构三角网格的局部加密方案试图验证其模拟精度。另外,为减小开边界的影响,我们把计算区域扩大,使开边界更远离模式输出点。
局部加密非结构三角网格分辨率由外至输出站点分别为:6'、2.5'、1',见图10。其中,共包含37602个节点和72701个三角形。模式所有参数设置同上文。用于验证的实测资料仍采用上文两个浮标测站的实测数据。模式输出从12月1日00时开始至12月15日00时结束,输出时间间隔为1小时。
不加密非结构三角网格运算耗时2小时21分钟,局部加密非结构三角网格运算耗时为5小时50分钟。可见网格点的增加使运算效率降低。而比较两者之间的相关系数、均方根误差、平均绝对误差可知,非结构三角网格局部加密方案可以提高模式的模拟精度,使模拟结果的均方根误差、平均绝对误差减小,模拟值和实测值间的相关系数增大(见表4)。

图8 矩形网格、非结构三角网格模拟黄渤海海域有效波高图 (单位:m)
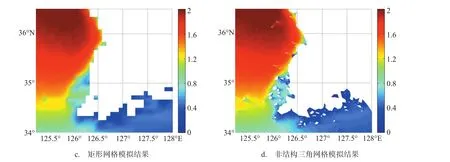
图9 矩形网格、非结构三角网格模拟黄渤海海域有效波高局部放大图(单位:m)
相关系数、均方根误差、平均绝对误差

表3 浮标22101处,不加密非结构三角网格、局部加密非结构三角网格模拟的有效波高结果间的

表4 浮标22102处,不加密非结构三角网格、局部加密非结构三角网格模拟的有效波高结果间的相关系数、均方根误差、平均绝对误差
图11中给出了不加密非结构三角网格和局部加密非结构三角网格模拟的有效波高随时间变化对比,可以看出,非结构三角网格局部加密方案模拟结果更符合实测值。
5 结论
本文先通过对输入风场的验证,保证了具有较高精度的风场输入,在此基础上分别采用矩形网格和非结构三角网格下的第三代海浪数值模式SWAN对我国黄渤海海域有效波高进行模拟。得出如下结论:
(1)海浪模式SWAN分别利用矩形网格和非结构三角网格对黄渤海有效波高模拟的结果与浮标实测资料均有较理想的吻合,表明运用两种不同网格,海浪模式SWAN都可以较好反映出黄渤海海域波浪变化情况;

图10 局部加密三角网格

图11 不加密非结构三角网格和局部加密非结构三角网格模拟的有效波高随时间变化对比图
(2)在模式各项设置和网格分辨率均相同的情况下,计算网格的选取仍可一定程度影响到模拟结果的精度。非结构三角网格相对于矩形网格可以使有效波高模拟结果的均方根误差、平均绝对误差减小,模拟值和实测值间的相关系数增大。这表明采用非结构三角网格较之矩形网格可以使SWAN模式模拟能力有一定程度的提升;
(3)较之于矩形网格,非结构三角网格可以不通过模式嵌套而实现对所关注区域局部加密,以保证关键区域的计算精度,进一步有效提升模式模拟能力。但局部加密方案增加了计算量,使运算效率有所降低;
(4)相对矩形网格,非结构三角网格对地形的刻画具有一定优势。采用非结构三角网格,模拟区域海岸线边界与实际拟合较好,近岸岛屿也较清晰,这在复杂海岸线地区体现的较明显。矩形网格则有一定欠缺。
需要指出的是,在实际海洋状态下,波-流相互作用和浅水区水位对水深的贡献是不容忽视的[12]。本文应用SWAN模式进行模拟实验,虽较全面考虑到诸多物理过程,但并没有考虑海洋环流和水位的影响。在今后工作中可以将海洋环流模式输出的流场和水位提供给海浪模式SWAN,以期进一步提高海浪模式模拟精度;本文的模拟研究仅限于黄渤海海域,仅选取了朝鲜半岛西侧海域的两个浮标实测数据作为验证资料,模拟时段内天气过程比较平稳,是否具有普适性还待做更多的个例研究。
[1]Melville,W K.The role of surface-wave breaking in air-sea interaction[J].Ann.Rev.Fluid Mech.,1996,28:279-321.
[2]Shi J,Zhao D L,Li X Q,et al.New wave-dependent formulae for sea spray flux at air-sea interface[J]. Journal of Hydrodynamics,2009,21(4):573-581.
[3]蒋小平,钟中,张金善等.台风Winnie(1997)影响下海浪的数值模拟研究[J].热带气象学报,2007,23(4):376-382.
[4]杨德周,尹宝树,徐艳青等.SWAN浅水波浪模式在渤海的应用研究-Phillips线性增长比例系数的改进[J].水科学进展,2005,16(5):710-714.
[5]梅婵娟,赵栋梁,史剑.两种海浪模式对中国黄海海域浪高模拟能力的比较[J].海洋预报,2008,25(2):92-98.
[6]胡克林,丁平兴,朱首贤等.长江口附近海域台风浪的数值模拟——以鹿沙台风和森拉克台风为例[J].海洋学报,2004,26(5):23-33.
[7]黄必桂.渤海海浪的数值模拟和涌浪对风浪影响的研究[D].中国海洋大学,2009.
[8]Qi J H,Chen C S,Beardsley Robert C,et al.An unstructured-grid finite-volume surface wave model (FVCOM-SWAVE):Implementation,validations and applications[J].Ocean Modelling,2009,28:153-166.
[9]Whitham G B.A general approach to linear and non-linear dispersive waves using a Lagrangian[J].J Fluid Mech,1965,22:273-283.
[10]Bretherthon F P,Garrett C J R.Wave trains in inhomogeneous moving media[J].Proc Roy Soc London,1968,A302:529-554.
[11] 葛义军,钟中,李杰.SWAN模式中谱空间离散方案对台风浪模拟的影响研究[J].海洋通报,2008,27(6):1-8.
[12] 蒋小平,钟中,张金善等.台风浪模拟预报中的风场比较研究[J].海洋通报,2007,26(2):11-19.
Comparison of ocean wave simulation with SWAN wave model using two kinds of computational grid in the Bohai Sea and the Yellow Sea
SHI Jian1,WANG Pu1,2,ZHONG Zhong1,ZHANG Jun1
(1.Institute of Meteorology,PLA University of Science and Technology,Nanjing 211101 China;2.72517 Troops of PLA,Jinan 250022 China)
Driven by the NCEP reanalyzed winds,the rectangular and unstructured triangular grids is applied respectively to the SWAN(Simulating Waves Nearshore)wave model based on the same physical processes and grid resolution to simulate the ocean wave field of the Bohai Sea and the Yellow Sea in December 2000.The simulated significant wave height is compared with the observed data from the buoys.The result demonstrates that the SWAN model used by both kinds of grids can reproduce reasonably the significant wave height.Comparing to that of the rectangular grid,application of the unstructured triangular grid can not only obtain better result,but also has the advantage of portraying the complex coastal regions.Moreover,a refined unstructured triangular grid is used by the SWAN model to simulate the ocean wave field,and the results show that the application of refined unstructured triangular grid can further improve the accuracy of the simulated significant wave height in the refined regions.
SWAN ocean-wave model;unstructured grid;significant wave height
P732
A
1003-0239(2011)04-0048-10
2010-10-26
史剑(1981-),男,讲师,主要从事海-气界面动力学研究工作。E-mail:shijian.mil@163.com
