删失相依数据下的分位数核估计的Bahadur型表达

王江峰，裘良华

（1.杭州师范大学理学院，浙江杭州 310036；2.杭州师范大学钱江学院，浙江杭州 310012）

删失相依数据下的分位数核估计的Bahadur型表达

王江峰1，裘良华2

（1.杭州师范大学理学院，浙江杭州 310036；2.杭州师范大学钱江学院，浙江杭州 310012）

该文考虑了在删失相依数据下分位数函数的核估计.在适当条件下，建立了该估计的弱和强Bahadur型表达形式.作为它的应用，导出了该估计的渐近正态性.通过模拟给出了该估计在有限样本下的表现.

渐近正态性；Bahadur型表达；删失数据；α－混合序列；分位数函数.

0 引 言

X1，X2，…和T1，T2，…是两个相互独立的非负随机变量序列，分布函数分别为F和G，这里｛Xi，i≥1｝和｛Ti，i≥1｝都是相依的随机变量序列.设Zi＝min（Xi，Ti）＝Xi∧Ti和δi＝I（Xi≤Ti），这里I（·）表示示性函数.在删失模型中，仅仅能观察到数据（Z1，δ1），…，（Zn，δn）.显然，Zi的分布函数

H（x）＝1－（1－F（x））（1－G（x））.令＝1－H和.在区间［0，∞）上定义两个随机过程如下：

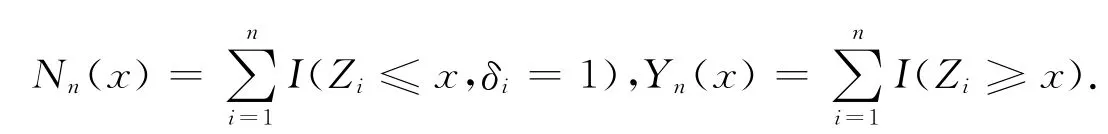
这样分布函数F的Kaplan－Meier（KM）估计为

这里dNn（s）＝Nn（s）－Nn（s－），Nn（s－）为Nn在s上的左极限.接下来，笔者给出分布函数F的p分位数的定义：Q（p）≡F－1（p）＝inf｛t：F（t）≥p｝，0≤p≤1.这样根据分布函数F的KM估计得到F的p分位数估计为

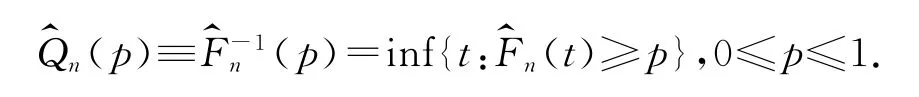
当（Xi）i≥1和（Ti）i≥1为独立同分布且相互独立时，Csörgö［1］和Cheng［2］在删失模型下得到了（p）的一些渐近结果.Ould－saïd和Sadki［3］在强混合条件下得到了（p）的Badadur型表达式.由于Q（p）为连续函数，因此用一个光滑估计比（p）更适用.Padgett［4］基于（p）上提出了Q（p）的一个核估计如下：

这里k（·）为核函数，hn为窗宽满足hn→0（n→∞）.在删失独立样本下，估计Qn（p）的性质有一些作者进行研究，可以参考Lio等人［5］和Lio和Padgett［6］.

据知，还没有人在删失相依数据下来研究Qn（p）的性质.该论文主要目的在删失相依数据下建立Qn（p）弱和强Bahadur型表达式，作为应用得到了Qn（p）的渐近正态性结果，并对估计进行模拟研究.

定义1 ｛ξk，k≥1｝称为α－混合序列，若当n→∞，

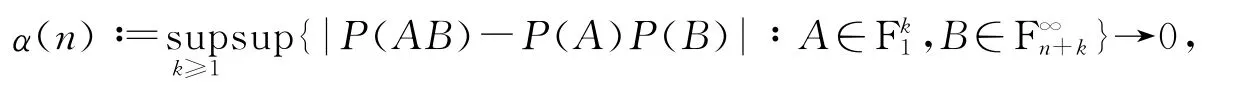
1 主要结果

这样，有E［ξ（Zi，δi，x）］＝0和Cov（ξ（Zi，δi，s），ξ（Zi，δi，t））＝g（s∧t）.设C为任意正数，在不同的地方可以表示不同的值.an＝O（bn）表示an≤Cbn.

为了得到结果，先给出一些条件：

（A1）（Xi）i≥1为平稳的α－混合序列，具有连续的分布函数F和混合系数α1（n）.

（A2）（Ti）i≥1i为平稳的α－混合序列，具有连续的分布函数G和混合系数α2（n）.

（A4）核函数k（·）为概率密度函数且在［－1，1］上紧支撑和∫tk（t）dt＝0.

（A5）F为Lipschitz连续的且密度函数为f.

（A6）对0＜p＜1，f（x）在x＝Q（p）上连续，并且有f（Q（p））＞0和Q（p）＜τH.

（A7）对0＜p＜1，F（x）在x＝Q（p）上具有连续的二阶导数.

注1 （A1）－（A7）都是一般性的条件.（A1）－（A3）和（A5）－（A7）在文献［3］中用到了.条件（A4）在文献［8］中应用到了.

注2 注意到以上条件不需要｛Ti｝是独立的，独立条件在文献［9］和［10］中应用到了.在他们的文献中，｛Xi｝的混合系数为a1（n）＝O（n－ν）（ν＞3），比条件（A3）要弱.但通过文献［11］的引理2知道，当｛Xi｝和｛Ti｝都为α－混合序列时，得到｛Zi｝仍然是α－混合序列且混合系数为4α（n），这样｛Zi｝满足文献［12］中定理3的条件.由于文献［9］中的结果和［10］中定理1的结果是通过文献［12］中的定理3证明过来的，因此他们的结果在以上条件下也是成立的.

下面先给出分位数Q（p）的核估计Qn（p）的弱Bahadur型表达式：

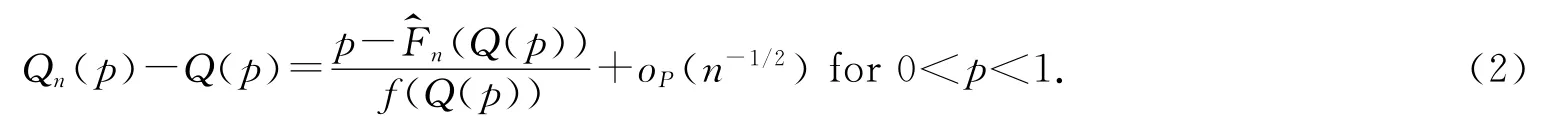
作为定理1的应用，可以通过文献［9］的定理5得到Qn（p）的渐近正态性：

推论1 在定理1的假设条件下，有

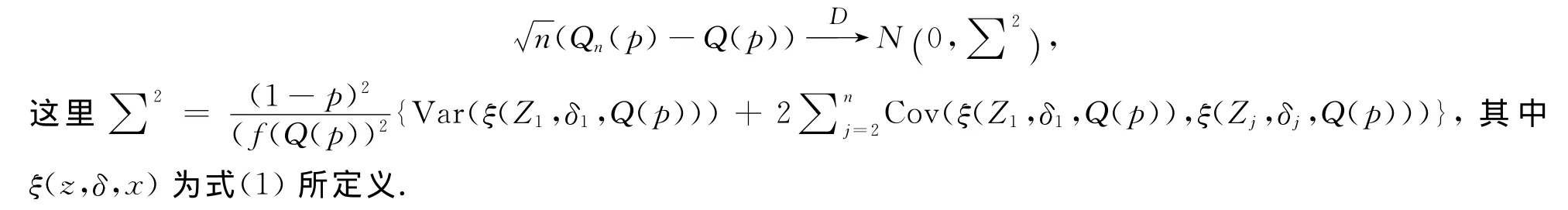
最后，给出Qn（p）的强Bahadur型表达式.

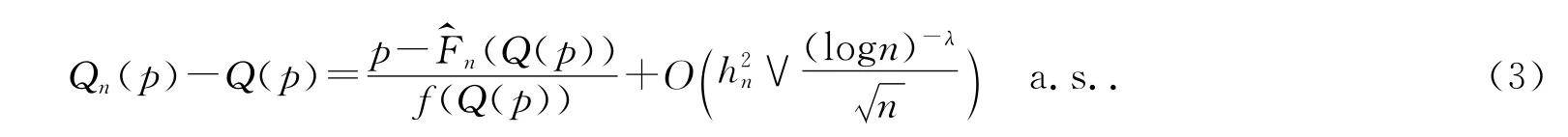
这里λ＞0.

2 模拟研究

在这一节，给出模拟来完成两件事情，首先，通过偏移和均方误差来比较估计Qn（p）和（p）；其次，给出估计Qn（p）在p＝0.5的渐近正态性的效果.

模拟X1～N（0，1/0.84），Xi＝0.4Xi－1＋ei，这里ei～N（0，0.82）.模拟T1～N（0，1/0.75），Ti＝0.5Ti－1＋ei.这样，Xi和Ti为α－混合序列，且混合系数都是以指数衰退的速度趋向零，并且它们的分布分别为N（0，1/0.84）和N（0，1/0.75）.显然这时删失比例为50%.

表1 Qn（p）和（p）的偏移和均方误差Tab.1 The bias and mean squared errors for Qn（p）and（p）

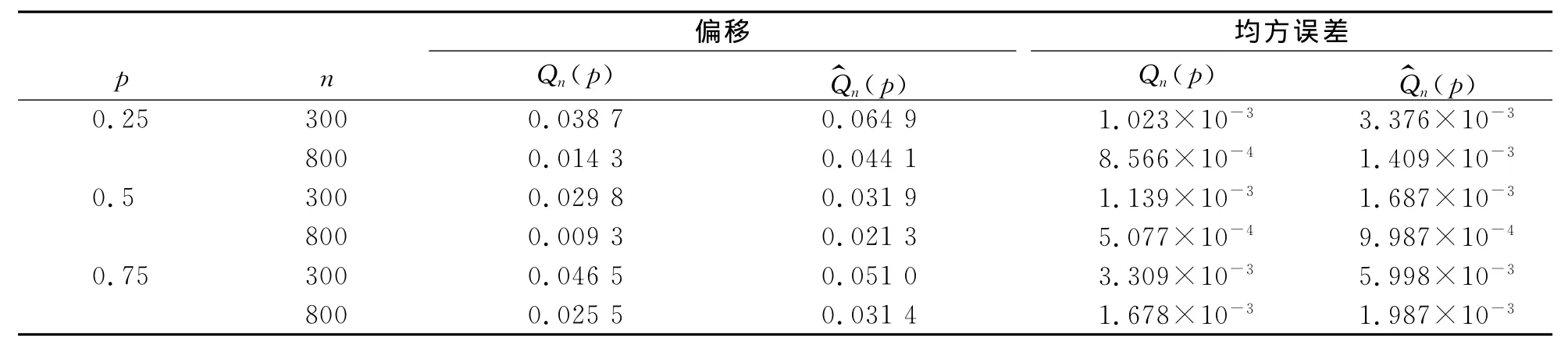
表1 Qn（p）和（p）的偏移和均方误差Tab.1 The bias and mean squared errors for Qn（p）and（p）

pn偏移Qn（p） Q＾n（p）均方误差Qn（p） Q＾n（p）0.25 300 0.038 7 0.064 9 1.023×10－3 3.376×10－3 800 0.014 3 0.044 1 8.566×10－4 1.409×10－3 0.5 300 0.029 8 0.031 9 1.139×10－3 1.687×10－3 800 0.009 3 0.021 3 5.077×10－4 9.987×10－4 0.75 300 0.046 5 0.051 0 3.309×10－3 5.998×10－3 800 0.025 5 0.031 4 1.678×10－3 1.987×10－3

从表1发现：（i）这两个估计都是随着样本容量n增大，效果越好.（ii）核估计Qn（p）模拟的效果比估计（p）好.接下来，通过直方图和正态概率图来模拟估计Qn（p）在p＝0.5的渐近正态性.在样本容量为n下独立地模拟了M＝1000个数据，选择窗宽hn＝n－1/3.在图1和2中，分别选取n＝200和800.从图1和图2看出样本容量n越大，模拟的效果越好.

3 定理的证明

为了证明以下结果，需要一些注记和引理.

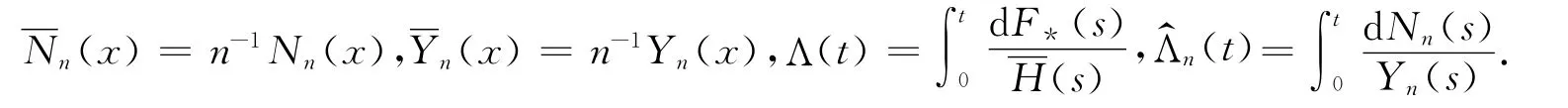
引理1 如果（A1）－（A3）和（A5）－（A6）满足，则

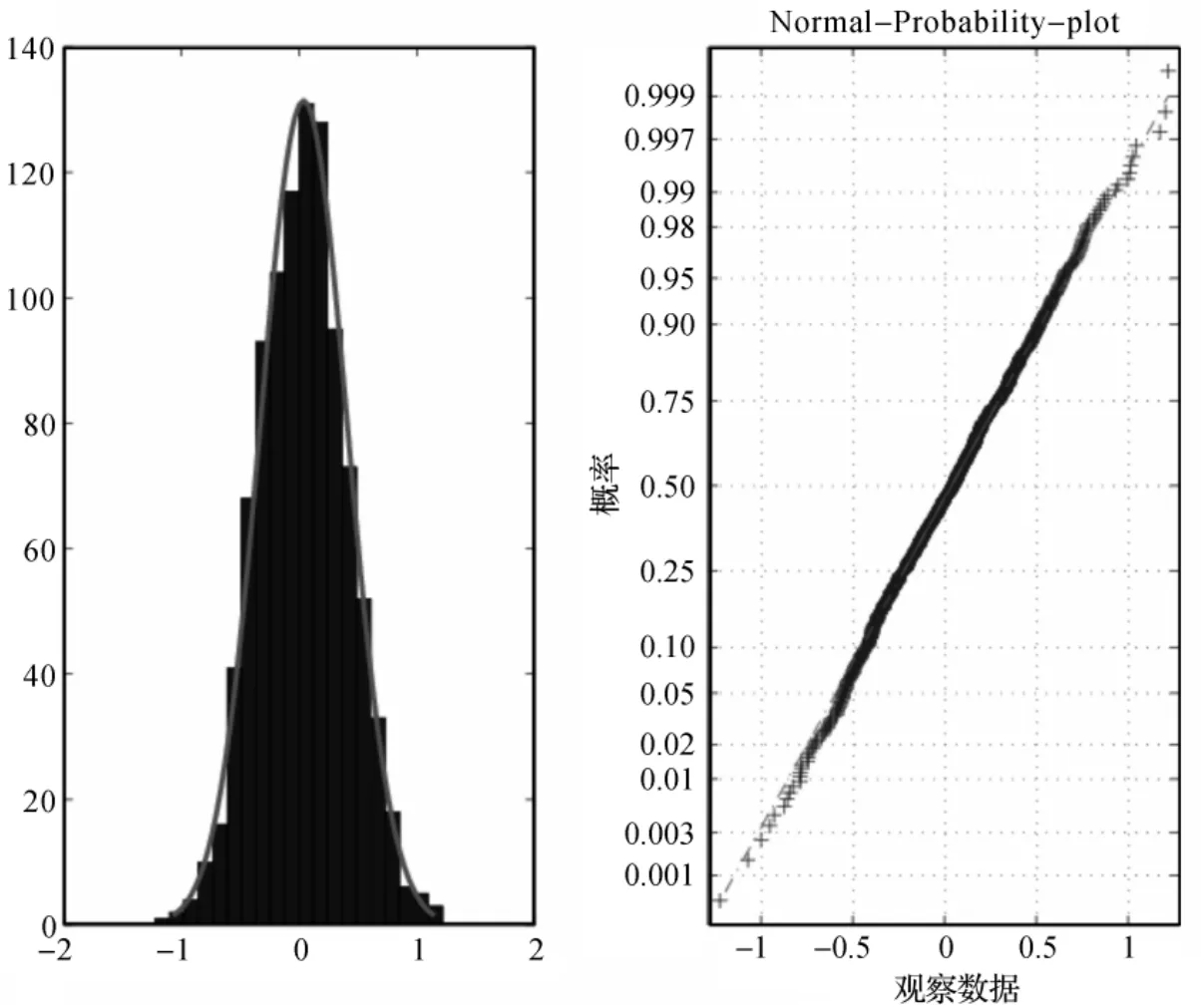
图1 在n＝200下Qn（p）的直方图和正态概率图Fig.1 Histogram and Normal－probability－polt of Qn（p）with n＝200

图2 在n＝800下Qn（p）的直方图和正态概率图Fig.2 Histogram and Normal－probability－plot of Qn（p）with n＝800

证明 设In＝［p－hn，p＋hn］and 0＜p0≤p1＜1.由文献［3］中的定理2.1和文献［10］中的定理1，得到

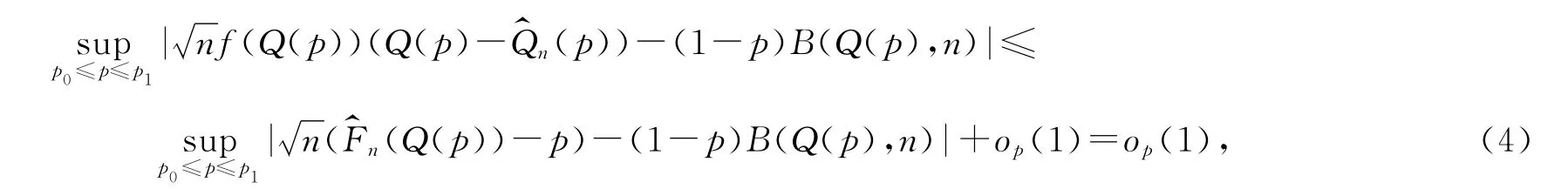
这里B（x，n）为文献［10］中的定理1所示.类似地，也可以证明

［1］CsörgöM.Quantile processes with statistical applications［C］//CBMS－NSF Regional Conference Series in Applied Mathematics，No.42，Philadelphia，1983.

［2］Cheng Kuangfu.On almost sure representation for quantiles of the product－limit estimator with applications［J］.Sankhyà，1984，46：426－443.

［3］Ould－saïd E，Sadki O.Strong approximation of quantile function for strong mixing censored processes［J］.Comm Statist Theory Methods，2005，34：1449－1459.

［4］Padgett W J.A kernel－type estimator of a quantile function from right－censored data［J］.J Amer Statist Association，1986，81：215－222.

［5］Lio Y L，Padgett W J，Yu K F.On the asymptotic properties of a kernel－type quantile estimator from censored samples［J］.J Statist Plann Inference，1986，14：169－177.

［6］Lio Y L，Padgett W J.Asymptotically optimal bandwidth for a smooth nonparametric quantile estimator under censoring［J］.J.Nonparametr.Stat，1992（1）：219－229.

［7］Doukhan P.Mixing：Properties and Examples［M］.New York：Springer－verlag，1994.

［8］Xiang Xiaojing.Bahadur representation of the kernel quantile estimator under random censorship［J］.J.Multivariate Anal，1995，54：193－209.

［9］Cai Zongwu.Asymptotic properties of Kaplan－Meier estimator for censored dependent data［J］.Statist Probab Lett，1998，37：381－389.

［10］Fakoor V，Jomhoori S，Azarnoosh H.Asymptotic expansion for ISE of kernel density estimators under censored dependent model［J］.Statist Probab Lett，2009，79：1809－1817.

［11］Cai Zongwu.Estimating a distribution function for censored time series data［J］.J Multivar Analysis，2001，78：299－318.

［12］Dhompongsa S.A note on the almost sure approximation of the empirical process of weakly dependent random variables［J］.Yokohama Math J，1984，32：113－121.

Abstract：asymptotic normality；Bahadur－type representation；censored data；α－mixing；quantile function.

Bahadur Type Representation for the Kernel Quantile Estimation of Quantile Funtion with Censored Dependent Data

WANG Jiang－feng1，QIU Liang－hua2

（1.College of Science，Hangzhou Normal University，Hangzhou 310036，China；
2.Qianjiang College，Hangzhou Normal University，Hangzhou 310012，China）

This paper considered the kerne estimation of the quantile function wtih censored dependent data.Under appropriate assumptions，the paper established the weak and strong Bahadur－type representations for the kernel estimation，derivd the asymptotic normality of the estimation and provided the representation of the estimation in firute samples via simulation

O211.4 MSC2010：60F15

A

1674－232X（2011）05－0385－08

10.3969/j.issn.1674－232X.2011.05.001

2011－04－23

国家自然科学基金项目（11001070）；浙江省教育厅科研基金项目（Y200906404）.

王江峰（1978—），男，江西南昌人，讲师，博士，主要从事统计推断方面研究.E－mail：wjf2929＠163.com