求解多维度背包问题的一种组合排序遗传算法

袁德辉，杨圣云，傅胤荣，赖国明

（韩山师范学院数学与信息技术系，广东潮州 521041）

求解多维度背包问题的一种组合排序遗传算法

袁德辉，杨圣云，傅胤荣，赖国明

（韩山师范学院数学与信息技术系，广东潮州 521041）

提出了一种组合排序方案，并将这种排序方案应用于遗传算法．利用该排序下的遗传算法针对OR数据库中的多维度背包问题进行了求解，同时和其它类似算法进行了实验比较.

多维度背包问题；组合排序；遗传算法；适应度函数；伪利用率

1 引论

众所周知，许多实际问题都可以归结为多维度背包问题（MKP），如资本预算问题[1]、分布式计算机系统中的处理器和数据库指派问题[2]、集装箱装载问题[3]、下料问题[4]等．因此关于求解多维度背包问题的研究经久不衰，特别是随着计算机技术的发展，这方面的研究变得更加活跃．所有背包问题在理论上属于NP-Hard问题，也就是说，有很大的可能性设计不出多项式时间解法[5]．目前背包问题解法大致上分为精确算法和近似算法两类．遗传算法及其改进方法[6-7]、蚂蚁优化算法[8]、属性论方法[9]等均属于近似算法范畴．多维度背包问题（MKP）的一般定义如下：

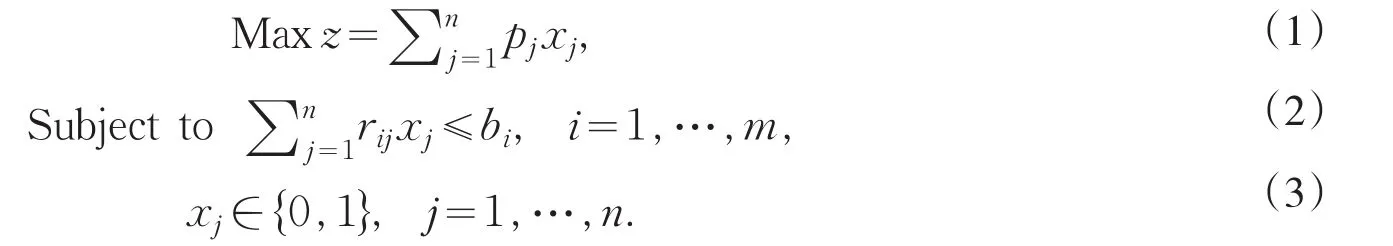
其中n表示变量的个数；m表示约束条件个数；pj表示第j个变量的受益量；bi表示第i个约束的预算；rij表示第j个变量占用第i个约束的量；xj表示0-1决策变量（当变量j被选择时xj=1，否则xj=0）．从以上模型可以看出，所有0-1整数线性规划问题都可以看成是一个背包问题，因此求解多维度背包问题就是求解上面的0-1整数规划问题．若将约束条件（3）改变为如下的条件（4）：

则MKP就是一般的线性规划问题（LP），称这个问题为MKP的松弛线性规划问题.

Chu和Beasley[10]根据伪利用率这种排序方式给出了求解多维0-1背包问题的遗传算法，获得了很好的计算结果．Raidl[11]则基于松弛线性规划（LP）的最优解给出了求解MKP的遗传算法．受文献[10-11]的启发，本文所提出的方法是先将以上0-1整数规划问题的解（可行或者不可行）依照一种组合利用率排序，然后在遗传算法求解的修复阶段利用这一排序将不可行解改造成可行解，进一步将可行解改进为更好可行解．最后利用这种新的遗传算法对MKP问题求解，以验证该遗传算法的有效性．

2 算法描述

2.1 一种新的组合排序

在遗传算法设计中，排序的重要性在于给定排序方案后，计算机就能够根据排序对子代（0-1规划的解子集）进行修复，以获得更好的子代（0-1规划的解子集），这是遗传算法求解MKP的关键所在.排序在某种程度上决定了最终结果的好坏程度.

Chu和Beasley[10]利用伪利用率设计了一个求解MKP问题的遗传算法，这里伪利用率定义为：

其中wi是MKP问题对应松弛线性规划（LP）的第i个约束的影子价格．利用这个排序对遗传算法中的修复操作进行指导，Chu和Beasley获得了很理想的计算结果．Raidl[11]从另外一个方面来理解物件的价值．在求解KMP问题时，先求解对应松弛线性规划问题得到LP问题的一个最优解．根据实验数据，Raidl观察到如果XLPi的值越大则这个物件被选中的可能性就越大．基于这个观察，他给出了一个改进的遗传算法[11]，该算法对背包问题也具有很高的求解能力.

受文献[10]和[11]启发，下面提出一种新的排序方案，称之为组合排序方案．这种方案同时兼顾伪利用率及最优解对应分量．定义第i个物件的组合利用率为：

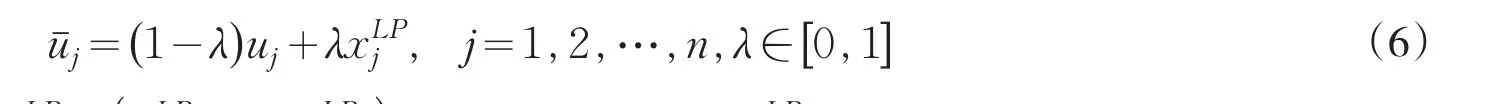
标准遗传算法采纳了自然进化模型，如选择、交叉、变异、修复、加强等．计算开始时，取一定数目（N个）解（0-1规划的解子集）（父解1，父解2，…，父解N），即种群随机进行初始化，并计算每个解（个体）的适应度，从而产生第一代即初始代．如果不满足优化准则，则开始产生新一代解（个体）的计算．为了产生下一代，按照适应度选择解（个体），父代解要求基因重组（交叉）而产生子代解．所有的子代按一定的概率变异．然后子代的适应度又被重新计算，子代被插入到种群中而取代父解，构成新的一代解（子解1，子解2，…，子解N）．循环执行这一过程，直到满足停止条件为止[7]．当步骤“修复”采用伪利用率所确定排序指导修复得到Chu和Beasly的遗传算法，当采用MKP对应松弛线性规划问题（LP）最优解所确定排序指导修复得到Raidl所讨论的遗传算法．采用由（6）所定义组合利用率对应排序指导修复工作，称对应遗传算法为组合排序遗传算法．由于无法获得文献[10]中详细算法实验框架，为此设计了如图1的算法框架：

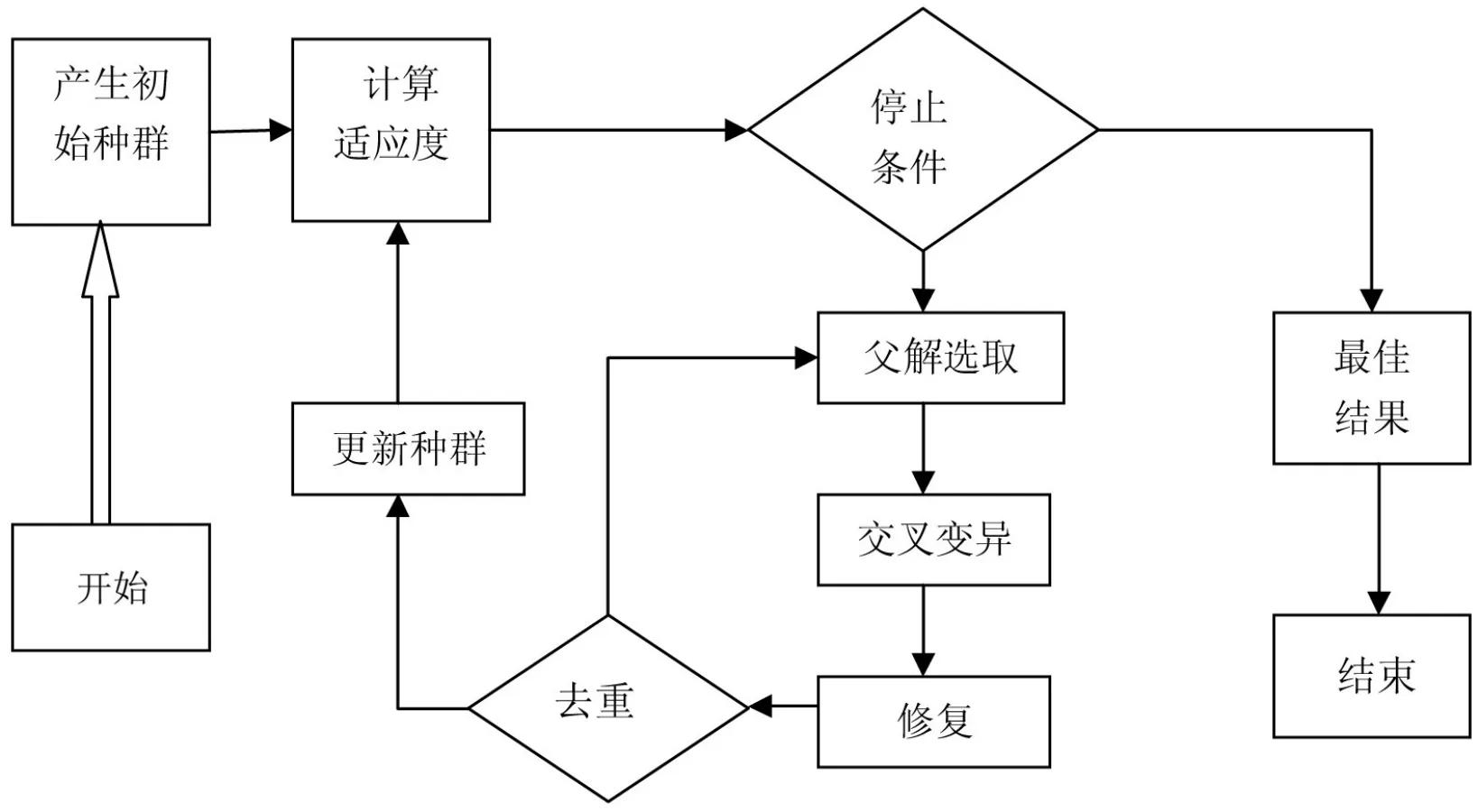
图1 遗传算法流程图

2.2 组合遗传算法的Matlab主程序

3 实验方案与结果比较

选取Chu等人提出的标准大规模数据集来测试组合序遗传算法，这是一个公开的数据集，可以从OR-Library上获得，网址是http://mscmga.ms.ic.ac.uk/info.html.这个数据集是由约束条件数m分别为5、10、30，变量数n分别为100、250、500，紧率α分别为0.25、0.5、0.75的多维度背包问题共270个组成，其中对每组给定的(m,n,α)有10个随机生成的背包问题样例.

实验使用Matlab软件在Pentium PC机上进行的，除m=5,n=100的30个问题样例各运行一次组合遗传算法和Chu的遗传算法外，其它240个样例均使用这两种遗传算法各运行10次，记录下运行的结果并用于统计，目的是验证组合排序遗传算法的效率，即组合排序方案的指导能力．对m=5,n=100的30个问题只运行一次，因为两个算法运行一次就得到了OR-Library提供的最佳结果，从而没有进行多次重复计算，因此表1中相应的AGap以及AMGap不存在．

正如在前一节中指出的那样，在图1所示的框架下，如果修复阶段采用伪利用率所确定的排序指导修复，则所得遗传算法本质上就是Chu等的算法．为更好进行算法性能比较，即不同排序的指导能力，本文同时按图1的框架用Matlab软件实现了Chu的算法．实验结果表明，组合排序具有非常好的指导能力.组合序遗传算法与Chu等人遗传算法详细的实验比较结果见表1．表1中NOPT表示使用相应算法所得结果达到或者超过OR-Library公布的Chu等人的最佳结果的样例个数，Nhc表示基于组合序遗传算法计算所得结果比基于Chu等人算法计算所得结果更好的样例数目，Nch则表示基于Chu等人算法计算所得结果比基于组合序遗传算法计算所得结果更好的样例数目，AGap表示对每组(m,n,α)的10个问题各运行10次所得共100个缝隙的平均值，AMGap是每组给定(m,n,α)10个问题每个运行10次所获得的最小缝隙的平均值.

从表1可以看出，组合序遗传算法在总体上要优于Chu的遗传算法：首先对同一个问题重复十次运行组合序遗传算法达到或者超过OR-Library公布的Chu等人的最佳结果的问题数就已经超过半数了，这不能不说是好的现象，因为OR-Library公布的最佳结果是在不知道重复了多少次遗传算法而获得的，而且这个数字也比Chu等人遗传算法运行十次就达到或者超过最佳结果的问题数目大了许多；其次就本文算法框架下实现的两个遗传算法做比较也可以看出Nhc要比Nch大，这说明组合序遗传算法总体上要比Chu等人遗传算法获得更为有利的计算结果．必须指出的是组合序遗传算法在计算第二组问题时没有显示其优势，不过在Chu等GA的计算结果也出现了同样的问题，这可能与这组数据特殊结构有内在的联系，这是接下来的研究中所要进一步考虑的问题．

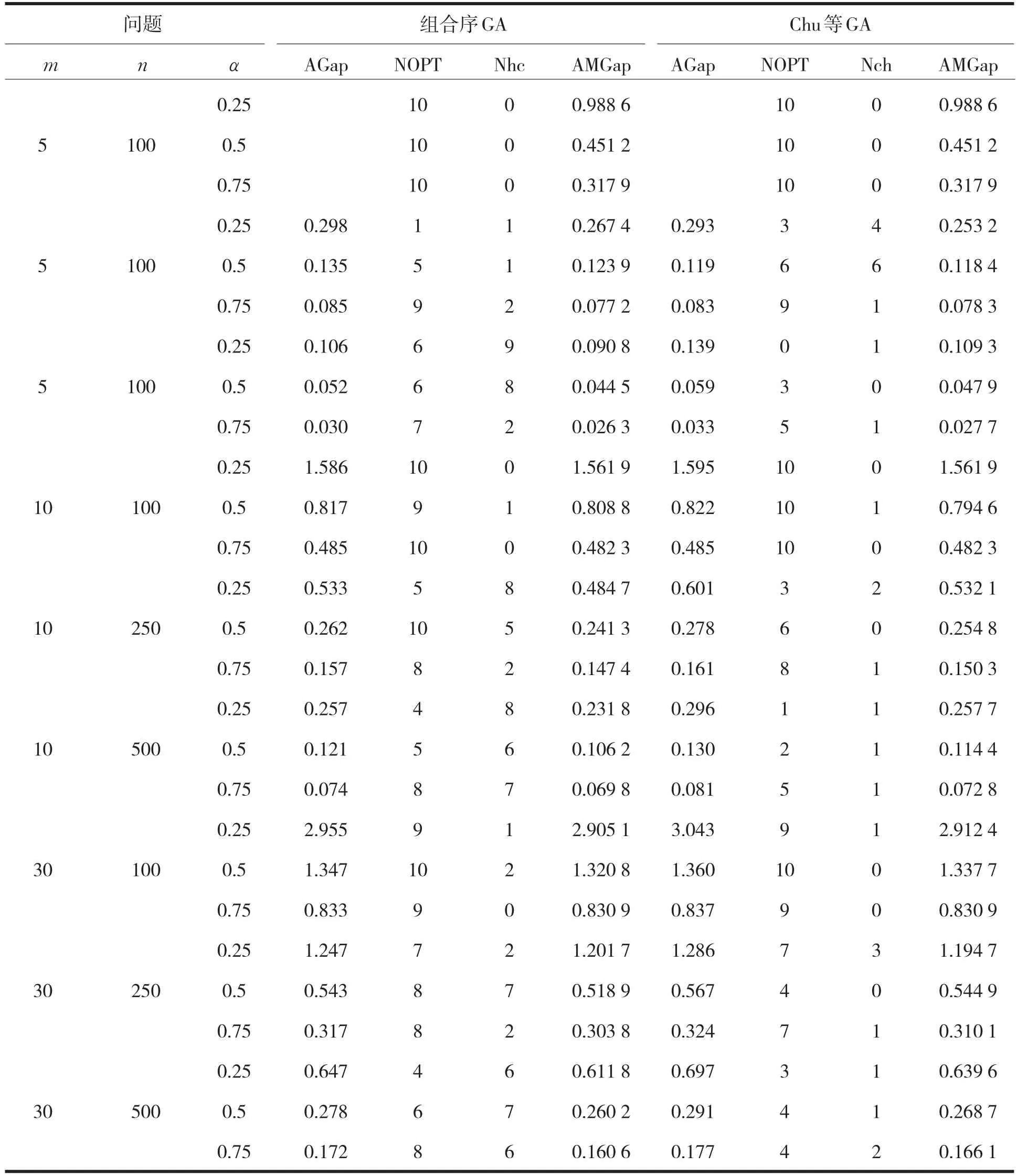
表1 组合序GA与Chu等人GA算法实验结果比较

[1]WEINGARTNER H M．Mathematical Programming and the Analysis of Capital Budgeting Problems[M].Chicago:Markham Publishing.1967：238-267.

[2]GAVISH B，PIRKUL H.Allocation of Databases and Processors in a Distributed Computing System[C].In J.Akoka(ed.)Management of Distributed Data Processing，North-Holland，1982:215-231.

[3]SHIH W.A Branch Bound Method for the Multiconstraint Zero-One Knapsack Problem[J].Journal of the Operational Research Society，1979，30:369-378.

[4]GILMORE P C，GOMORY R E.The Theory and Computation of Knapsack Functions[J].Operations Research，1966，14:1045-1075.

[5]KOLESAR P J.A branch and bound algorithm for the knapsack problem[J].Management Science，1967，13:723-735.

[6]曾智，杨小帆，陈静，等．求解多维0-1背包问题的一种改进的遗传算法[J]．计算机科学，2006，33（7）：220-223．

[7]姚瑞枫，宋玉阶．多维0-1背包问题的混合遗传算法[J]．武汉科技大学学报（自然科学版），2003，26（2）：214-217．

[8]马良，王龙德．背包问题的蚂蚁优化算法[J]．计算机应用，2001，21（8）：4-5.

[9]郑杨凡．基于属性论方法的0-1背包问题算法研究[D]．上海：上海海事大学图书馆，2005：10-55.

[10]CHU P C，BEASLEY J E.A genetic algorithm for the multidimensional knapsack problem[J].Journal of Heuristic，1998，4：63-86.

[11]RAIDL G R.An Improved Genetic Algorithm for the Multiconstrained 0-1 Knapsack Problem[C].In Proceedings of the 5th IEEE International Conference on Evolutionary Computation，1998，207-211.

A Genetic Algorithm Base on a New Order for Multidimensional Knapsack Problem

YUAN De-hui，YANG Sheng-yun，FU Ying-rong，LAI Guo-ming
(Institute of Mathematics and Information Technology，Hanshan Normal University，Chaozhou 521041，China)

The paper presents a new order for the multidimensional knapsack problem.Using this new order，we design an improved genetic algorithm.Computational results show that the new genetic algorithm is capable of obtaining high-quality solutions for MKP.Computational results also show that this algorithm gives superior quality solutions than Chu's.

multidimensional knapsack problem；combining ordering；genetic algorithm；fitness function；pseudo utilization

O224

A

1007-6883(2011)06-0022-07

2011-10-14

国家自然科学基金（30800244）资助项目,广东省自然科学基金（10152104101000004）资助项目,韩山师院团队科研（LT200801）资助项目.

袁德辉（1973－），男，江西赣州人，韩山师范学院数学与信息技术系副教授.

责任编辑 朱本华