结构转变、资本深化与生产率增长
2011-12-21李文兵
李文兵
(华中科技大学经济学院,湖北 武汉 430074)
结构转变、资本深化与生产率增长
李文兵
(华中科技大学经济学院,湖北 武汉 430074)
通过构建劳动生产率和TFP增长的分解方程,强调了结构转变通过劳动在不同部门间的重新配置以及不同部门间资本深化的效率差别对生产率的影响,重新考察了我国改革开放以来结构转变与生产率增长之间的关系。结果表明无论以劳动生产率还是TFP作为生产率的度量指标,我国的三次产业结构转变并没有导致显著的“结构红利假说”现象,生产率的增长主要来自产业内部的资本深化;要素再配置效率的下降,尤其是差别资本深化效应为负是造成结构转变效应逐期下降的主要原因。
生产率;结构转变;结构红利;资本深化
1 引言
发展经济学认为结构转变是经济长期增长的重要源泉,没有各种要素在不同经济部门间的充分转移,获得人均产出的高增长率是不可能的。
本文在已有研究的基础上,采用了一种新的劳动生产率分解方法,强调了结构转变对资本深化和全要素生产率增长的影响,就中国三次产业的结构变动对劳动生产率增长的作用进行了分析。利用这一分解方法估计并分解了中国全要素生产率的增长率(TFPG),使之包含了要素再配置效应项,来捕捉结构变动的增长效应(即结构红利)。
2 分解方程
在这一部分,我们将构建劳动生产率以及TFP增长的分解方程。这一分解方程基于 Massel、Ohkawa、Denison和Chung、Jorgenson等以及Pilat等人的研究[1-5]。


其中,sYi和sLi分别表示部门i的产出和劳动在总产出和总的劳动投入中的份额。用G(Yi)=G(yi)+ G(Li)代入式(1),可得:

这里,ΔsLi=sLi[G(Li)-G(L)],表示每单位时间部门劳动份额的变化。式(2)右边第一项表示各部门劳动生产率增长率的加权平均。第二项表示劳动在不同部门间的再配置对劳动生产率的影响,如果劳动从低生产率(yi﹤y)向高生产率部门(yi﹥y)转移,此时高生产率部门吸收劳动(ΔsLi﹥0),而低生产率部门则释放劳动(ΔsLi﹤0),那么第二项为正,就会促进劳动生产率的提高。
传统的增长核算可表示为要素的贡献加上一个“索洛余量”(TFP),用公式表示为:G(y)=αG(k)+ TFPG,其中α表示资本的份额,TFPG表示TFP的增长率。G(k)表示人均资本的增长率,我们可以用得到式(2)的相同方法得到其分解方程:

式(3)表明人均资本的增长率不仅受到各部门内部资本深化的影响,而且取决于部门间要素再配置效应的影响。也就是说,如果部门的人均资本保持不变,即G(ki)=0,劳动从低人均资本向较高人均资本的部门转移((ki-k)ΔsLi﹥0),也会提高整个经济的人均资本,从而使得经济在资本深化的过程中并不必然的导致资本回报率的下降。我们可把该式右边的第一项和第二项分别叫作部门内部的资本深化效应和部门间资源再配置的资本深化效应。
下面对TFP的增长率进行分解。把式(3)代入到传统的增长核算方程,可得:

结合式(2)和式(4),我们便可以得到关于TFPG的分解方程:

式 (5)右边第一项括号里的表达式与传统的TFP增长率方程比较相似。如果要素在部门间是自由流动的,那么所有部门都将面临相同的要素价格,因而式(5)右边第一项括号里的表达式的值为零。如果要素的流动是有限制的,部门间的边际产品价值就存在差别,对于部门i来说,这个表达式的值就不为零。尤其当部门的工资率、资金的租赁价格或两者都高于整体经济的平均水平时,这个表达式的值就为正,即对TFP增长的贡献为正。因此,当资源从低生产率部门向高生产率部门转移,资源的配置效率就会提高,从而促进TFP的增长。我们可以把这一项称为资源再配置的效率效应。
为了进一步说明式(5)第二项所表达的涵义,我们利用传统的部门增长核算方程,即G(yi)=αiG(ki)+TFPGi,对其进行进一步的分解,可得:
其中,ri表示部门i的资本回报率。如果相对资本回报率较高的部门(ri﹥r)有相对较快的资本深化(G(ki)﹥G(k)),则式(6)右边第三项的值就为正,对TFP增长的贡献为正;反之如果相对资本回报率较低的部门(ri﹤r)有相对较快的资本深化(G(ki)﹥G(k)),则其值为负,对TFP增长的贡献为负。这一项可称之为部门间差别资本深化的效率效应。因此,式(6)右边第一项和第三项之和就表示结构变动对TFP增长的效应。
结合式(4)和式(6),我们便可得到劳动生产率增长的分解方程:

这一分解方程把劳动生产率增长分为了5部分:①第一项表示部门内部的资本深化效应;②第二项表示部门间资源再配置的资本深化效应;③第三项表示部门内部的TFP增长;④第四项表示部门间差别资本深化的效率效应;⑤第五项表示资源再配置的效率效应。在这个分解方程里,第一项和第二项之和表示资本深化效应,后面三项之和则表示TFP增长效应,而第二、四、五三项之和则表示结构转变效应。
3 数据处理及说明
根据上述分解方程,要对我国的劳动生产率增长率进行分解我们需要以下5类数据:产出、资本投入、劳动投入、资本收入份额以及资本回报率。下面对这些数据的来源和处理作一个简单的说明。
3.1 产出
目前,国内学者对产出数据的处理主要有两种方法,一是用增加值作为产出的指标,二是选择总产值作为产出的指标。本文采用用增加值作为产出的指标,并换算成1978年的不变价。
3.2 劳动投入
劳动投入应当是一定时期内要素提供的 “服务流量”,包含劳动数量、劳动质量、劳动强度、劳动效率等因素。在市场经济条件下,劳动报酬能较为合理地反映劳动投入,国外也一般用工作小时数和劳动工资来衡量劳动对产出的贡献。由于中国处于经济体制转型期,收入分配体制不尽合理并且市场经济体制不够完善,劳动报酬并不能合理反映劳动投入的差别,并且我国也没有工作小时数的统计数据,因此考虑到数据的可获得性、准确性和一致性,本文采用从业人数作为劳动投入的数据,这也是国内学者普遍采用的一种处理方法。
3.3 资本投入
资本投入用资本存量来衡量,目前国际上测量资本存量的通用方法是永续盘存法(PIM)。目前大多数OECD国家都有官方的资本存量数据,但中国还没有可用的官方资本存量数据。在学术界目前有很多关于资本存量测量的研究,大多都采用永续盘存法。大部分研究主要集中于测算全国的资本存量,对各个产业资本存量进行估计的文献较少,徐现祥、周吉梅、舒元用永续盘存法系统估计了我国1978—2002年各省区三次产业的物质资本存量[6]。因此,本文也根据国内外学者常用的永续盘存法将徐现祥等的估算序列从2002年更新到2005年,把各产业资本存量的加总作为全社会资本存量。定义本期的资本存量等于上期的资本存量加上当年的投资,再减去折旧,用公式表示为:

Kit表示第i产业第t年的资本存量,Iit表示第i产业第t年的投资,Ki,t-1表示第i产业t-1年的资本存量,Dit表示当年的折旧。因此,对2003—2005年各产业资本存量的估算需要以下数据:当年投资、固定资产投资价格指数以及资本折旧。本文对这些数据作如下的处理。
与Young和张军等的选择一样,徐现祥等也将各个产业的固定资本形成总额作为度量当年投资的指标。由于 《中国国内生产总值核算历史资料1952—2004》只提供了1978—2002年三次产业的固定资本形成总额,并且《中国统计年鉴》也只提供了2003—2005年分省的固定资本形成总额,而没有提供分产业的固定资本形成总额。但《中国统计年鉴》却提供了按行业分的全社会固定资产投资的数据,因此本文用固定资产投资作为当年的投资来估算2003—2005年的资本存量。从全社会固定资产投资与固定资本形成总额的对比来看,两者的差别不大,因此用固定资产投资来代替固定资本形成总额不会造成前后估算上的巨大差异。
我国的固定资产投资价格指数从1991年才开始统计,因此一些学者对于之前的固定资产投资价格指数进行了估算,如何枫等、Wang和Yao、龚六堂和谢丹阳、张军等利用《中国国内生产总值核算历史资料1952—1995》提供的数据计算了1952—1995年的固定资产投资价格指数。因此1991年之前的固定资产价格指数本文将直接采用张军等的估计,而1991年之后的则直接采用《中国统计年鉴》公布的固定资产投资价格指数。
对于折旧Dit,为了和徐现祥等保持一致,这里仍然按照《中国国内生产总值核算历史资料1952—2004》在按照收入法核算国内生产总值时提供的折旧数据来确定各个产业的折旧,但其只有2003—2004年的折旧数据,对于2005年各产业的折旧我们假定其以2003—2004年的折旧速度递增。
3.4 资本收入份额
最后,我们还需要资本收入在国民收入中所占的份额,即资本份额的数据。由于国民收入被分成了劳动收入和资本收入两个部分,因此,资本收入就是指国民收入剔除劳动报酬后的部分。《中国统计年鉴》提供了各省劳动者报酬的数据,但没有提供全国的劳动者报酬数据。因此,本文采用白崇恩(2006)的方法用各省劳动者报酬占GDP的份额按其GDP进行加权平均后得到的值作为全国劳动收入份额的数据[7]。其中,1978—1995年的分省劳动者报酬数据来自Hsueh和Li[8],1996—2005年的数据来自各年的《中国统计年鉴》。其中缺失了2004年的数据,我们用2003年和2005年的平均值来代替。
3.5 资本回报率
目前国内已有少部分研究我国资本回报率的文献,如白崇恩、谢长泰和钱颖一,单豪杰、师博,辛清泉、林斌和杨德明以及CCER“中国经济观察”研究组等。由于计算资本回报率比较复杂,本文不再重新测算,而是直接采用白崇恩等的研究结果。
4 实证结果分析
根据式(7)的分解方程以及产出,资本投入、劳动投入、资本收入份额以及资本回报率的相关数据,我们对中国1979—2005年的劳动生产率以及TFP增长进行了分解,其结果见表1。
从表1中可以看出,1979—2005年我国劳动生产率的平均增长率为 7.61%,1979—1989年为6.58%,1990—1999为 8.03%,2000—2005年 为8.66%,呈现出逐期提高的趋势。其中资本深化对劳动生产率增长的贡献非常高,在整个分析期达到了58.5%,同样也表现出逐期提高的趋势,从20世纪80年代的51%、90年代的59.5%增长到了2000—2005年的68%。换句话说,TFP增长对劳动生产率增长的贡献出现逐期递减的趋势,也就是说80年代的TFP增长对劳动生产率增长的贡献最高,达到了49%,几乎与资本深化效应对劳动生产率增长的贡献相一致。其可能原因如表2所示,在这一时期三次产业部门的TFP都实现了正增长,并且劳动份额最大(64.93%)且占GDP相对较大份额(23.78%)的农业部门保持着相对较高的TFP增长率(1.12%)。而之后农业部门的TFP增长率出现逐期下降,与此相对应的,农业部门的就业份额和实际产出份额分别从1978年的70.52%和28.18%下降到了2005年的40.84%和6.14%。而与此同时,第二产业的劳动生产率与TFP增长率却出现明显的加速增长,并且第二产业的就业份额和实际产出份额分别从17.29%和47.87%上升到了2005年的26.79%和65.96%。这表明从农业向第二产业的结构转变加速了整个经济的资本深化和生产率增长。
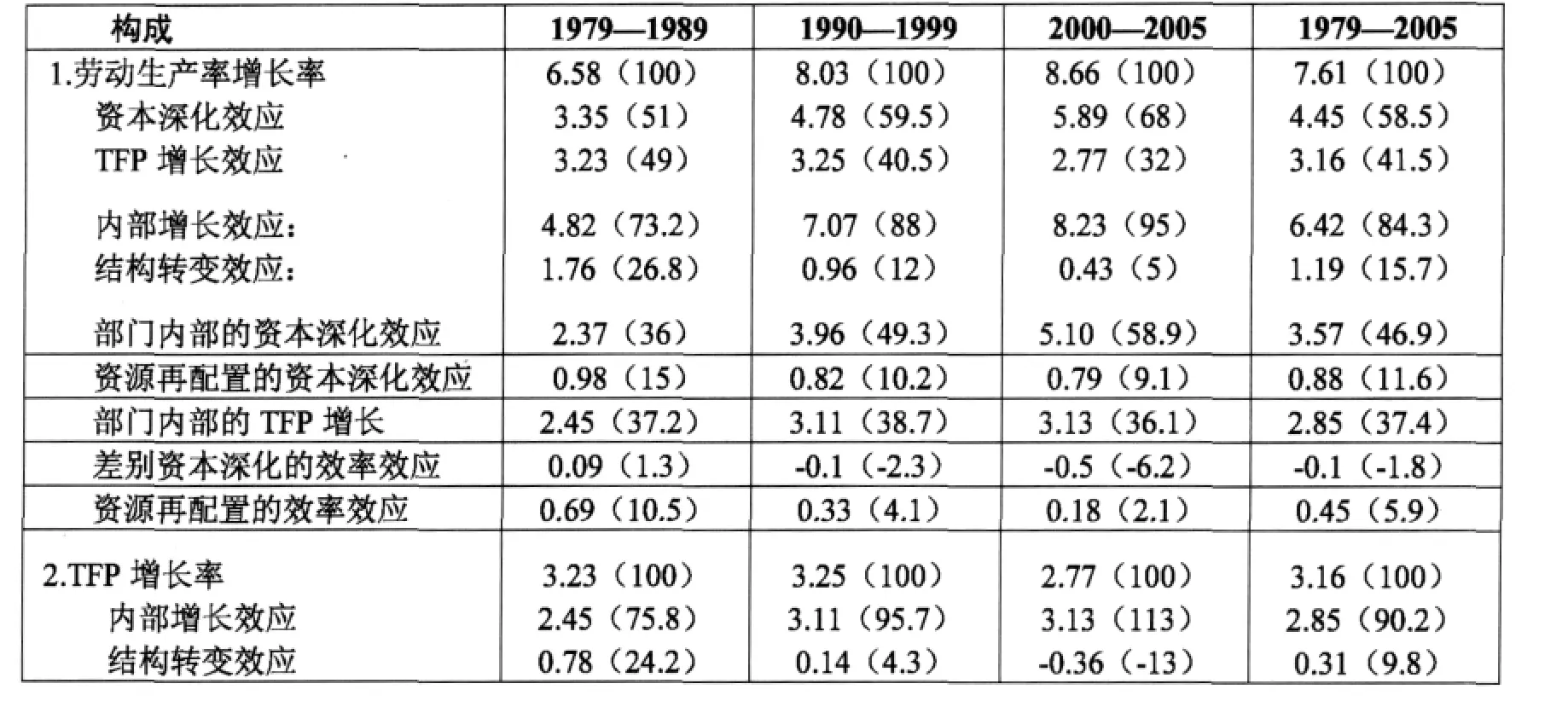
表1 我国三部门劳动生产率及TFP增长分解(%)
表1的第一部分给出了劳动生产率增长的各个分解部分。在整个分析期,中国的劳动生产率增长率为7.61%,其中内部增长效应对劳动生产率增长的贡献为84.3%,结构转变效应为15.7%,这说明中国劳动生产率增长主要来自于各个产业自身劳动生产率的提高,而资源再配置的结构转变效应相对较小。从不同的时期来看,结构转变效应对劳动生产率增长的贡献呈现出逐期下降的趋势,这表明随着产业结构的不断演进,我国的“结构红利”越来越小。在结构变动对劳动生产率增长的影响当中,资源再配置的资本深化效应虽然在逐期递减,但在三个时期差别不大,并且都为正,其增长率稳定在0.79%~0.98%之间,对劳动生产率增长的贡献在9%~15%。这表明资源再配置的资本深化效应的逐期缓慢递减并不是造成结构转变效应大幅下降的主要原因。从各部门人均资本的变动趋势可以看出,在20世纪80年代,农业和工业服务业的人均资本相差不大,随着经济的发展和结构转变,农业部门的就业人数不断下降,其他部门的就业人数则不断上升,而与此同时,农业部门的人均资本却没有出现大幅上升,其他部门的则呈现不断加速上升的趋势。因此,现代部门(高生产率)的资本深化使得资源再配置的资本深化效应为正,从而促进了劳动生产率的提高。
资源再配置的效率效应的增长率为0.45%,对劳动生产率和 TFP增长的贡献分别为 5.9%和14.24%。从趋势来看,其对劳动生产率和TFP增长的贡献也在逐期递减。造成这一效应为正的一个主要原因就是劳动从低生产率的农业部门转移到高生产率的部门。
差别资本深化的效率效应在整个分析期以及20世纪90年代和2000—2005年这两个时期的增长率分别为-0.14%、-0.19%和-0.54%,对劳动生产率的贡献分别为-1.8%、-2.3%和-6.2%,这说明差别资本深化的效率效应为负并且持续恶化是造成中国结构转变效应逐期下降的主要原因。造成这一效应为负的一个重要原因可能是从90年代以来,我国开始出现了加速资本深化的趋向,工业和服务业人均资本的增长速度非常快(见表2),尤其在这一时期我国基础设施建设的投资力度前所未有,比如公路、铁路、电力等行业得到了快速发展,而这些行业的一个显著特征就是具有较高的人均资本以及较低的资本回报率(ri﹤r),因而这些行业的快速资本深化(G(ki)﹥G(k))使得差别资本深化的效率效应为负。
差别资本深化的效率效应为负,表明在这两个时期资本并没有从低生产率的部门向高生产率的部门转移。在结构转变和经济加速资本深化的过程中,金融部门和金融市场在其中扮演着非常重要的作用。大部份文献的研究都表明金融发展能够促进生产率增长,Greenword和Jovanovic在分析金融和增长之间的关系时,强调了金融体系可以通过选择和资助经济中有效率的项目来提高整个经济的生产率[9]。但我们的研究并不支持上述观点,差别资本深化的效率效应为负表明我国的金融部门和金融市场把资本引导和配置到了低效率的部门,这一方面可能与我国所处的发展阶段有关,在经济发展的早期基础设施建设对快速工业化和经济增长至关重要,因此,相当一部分资本被配置到了诸如公路、铁路、电力等具有低资本回报率的基础设施行业;另一方面可能与我国的金融体制有关,高度垄断的国有金融体系将大部分资本都投入到了低效率的国有经济部门。这可从服务业的TFP增长率为负得到佐证,由于大部分基础设施和国有垄断行业属于第三产业,因而差别资本深化的效率效应为负导致了服务业的TFP出现了负增长。而基础设施建设却有利于第二产业的增长,因而第二产业的劳动生产率和TFP在各个分期内都实现了快速的正增长(见表2)。
下面我们把TFP作为度量生产率的指标来考察结构转变对生产率的影响。从表1的第2部分可知,我国的生产率增长主要还是来自各产业内部的TFP增长,结构转变的贡献甚微,只有不到10%,并且也呈现出逐期下降的趋势。在2000—2005年,结构转变对生产率增长的贡献为负,造成这一结果的主要原因是差别资本深化的效率效应为负。这说明在这一时期,我国出现了“结构负利假说”现象。
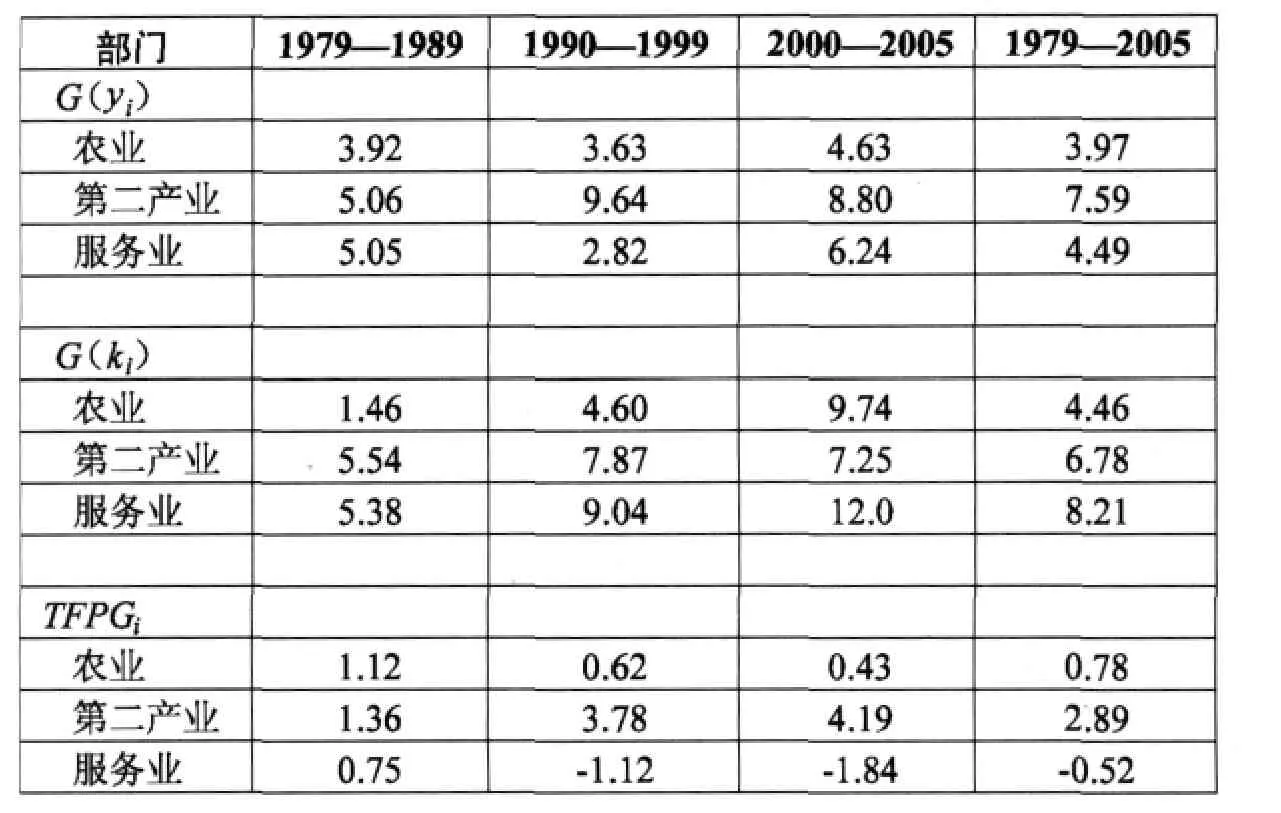
表2 劳动生产率、人均资本及TFP的年均增长率(%)
从上述分析可知,无论以劳动生产率还是以TFP作为度量生产率的指标,在整个分析期内我国均存在“结构红利”,但结构转变效应很小并呈现出逐期下降的趋势。在1978—2005年,资源从农业部门逐渐向其他部门转移的过程中,相当一部分资源被配置到了低生产率行业和基础设施行业,由于这些部门的资本回报率要低于整个经济的平均水平,因此差别资本深化的效率效应很低甚至为负。但同时我们也发现,资源从农业部门向工业和服务业部门的转移对生产率的提高具有一定的作用,资源再配置的资本深化效应和资源再配置的效率效应都为正,从而使得结构转变效应为正。所不同的是,以TFP为度量生产率的指标时,我国的“结构红利”要比以劳动生产率为度量指标时更小,并且在2000—2005年出现了“结构负利”现象。因此,改革开放以来,我国的结构转变并没有导致显著的“结构红利假说”现象。
5 结论
(1)改革开放以来,伴随着经济结构的变动,我国的劳动生产率呈现出逐步提高的趋势,但TFP增长对劳动生产率增长的贡献始终没有超过要素投入增长的贡献,并且其贡献度逐期下降,其主要原因在于要素再配置效率的恶化,劳动生产率的提高主要来自部门内部的资本深化。
(2)资源从低效率向高效率部门的转移,尤其是从传统部门向现代部门的结构转变对生产率的提高有着一定的作用。但这种结构转变效应随时间而下降,并且结构转变对生产率的影响在经济发展的不同时期以及不同部门之间存在显著差别。在改革开放的初期结构转变效应较为明显,之后则不断下降。生产率的增长主要来自产业内部生产率的提高,其中第二产业的贡献最大,并且结构转变对第二产业生产率提高的作用最大,对服务业生产率的提高却起到了一定的阻碍作用。
(3)我国三次产业间的结构转变并没有导致显著的“结构红利假说”现象,尤其当以TFP作为生产率的衡量指标时,在2000—2005年甚至出现了“结构负利”现象。其主要原因是在三次产业间的资源再配置中,相当一部分资本要素被配置到了低效率的行业,从而造成了差别资本深化效应出现了负增长。导致这种现象的原因可能与我国经济的发展阶段和高度垄断的国有金融制度有关。
[1]Massel B.F..A disaggregated view of technical Chang[J].Journal of Political Economy,1961,(69):547-557.
[2]Denison E.F.,Chung W.K..Economic growth and its sources[J].The Brookings Institutions,Washington,DC,1976,53-151.
[3]Ohkawa K..Effects of changes in allocation of production factors on macroeconomics productivity gains[J].Economic Review,1967,(18):346-349.
[4]Jorgenson D.W.,Gollop F.M.,Fraumeni B.M..Productivity and US Economic Growth[M].Harvard University Press,Cambridge,MA,1987.
[5]Pilat D..The sectoral productivity performance of Japan and the US,1885-1990[J].Review of Income and Wealth,1993,(39):357-375.
[6]徐现祥,周吉梅,舒元.中国省区三次产业资本存量估计[J].统计研究,2007,(5).
[7]Chong-en Bai,Chang-tai Hsieh,Yingyi Qian.The return to capital in China[J].Brookings Papers on Economic Activity,2006,(2):61-88.
[8]Hsueh,Tien-Tung,Li.China's National Income:1952-1995[M].Boulder:Westview Press,1999.
[9]Greenwood J.,Jovanovic B..Financial development,growth,and the distribution of income[J].Journal of Political Economy,1990,(98):1076-1107.
Structural Change,Capital Deepening and Productivity Growth
Li Wenbing
(School of Economics,Huazhong University of Science and Technology,Wuhan 430074,China)
Based on the debate about the existence and significance of“structural bonus hypothesis”,this article re-examines the relationship between structural change and productivity growth since 1978 by constructing a decomposition formula of productivity and TFP growth,which highlights the effects of labor reallocation and differential capital deepening due to structural transformation on productivity.The results show that either labor productivity or TFP being the productivity indicator,structural change did not cause the significant “structural bonus hypothesis”phenomenon;productivity growth mostly came from capital deepening within the industries;further decline in factor reallocation efficiency,particularly the negative effect of differential capital deepening is the main reason for the decline in effect of structural change.
productivity;structural change;structural bonus;capital deepen
国家社科基金重大项目《推进我国工业化与信息化融合研究》(08&ZD037)资助。
2010-10-19
李文兵(1979-),男,浙江温岭人,华中科技大学经济学院博士研究生;研究方向:宏观经济。
F064
A
(责任编辑 胡琼静)
