秦简《数》之“秏程”、“粟为米”算题研究*

肖 灿

(1.湖南大学 建筑学院,湖南 长沙 410082; 2.湖南大学 岳麓书院,湖南 长沙 410082)

秦简《数》之“秏程”、“粟为米”算题研究*

肖 灿1,2

(1.湖南大学 建筑学院,湖南 长沙 410082; 2.湖南大学 岳麓书院,湖南 长沙 410082)

叙述了对岳麓书院藏秦简《数》的算题“秏程”和“粟为米”的编连和研究。这两例算题记载了舂米的损耗和粟米的换算,反映了秦代粮食加工、交换、仓储等事务中的一些细节,验证了在上古时代“石”这一单位具有特殊性的观点。

秏程;粟为米;《数》;秦简

秦简《数》不是通过科学的考古发掘得到的,这使得秦简《数》缺失了很多的简文信息和有关各条之内、各条之间关系的信息,也缺失了与之相关的墓主个人及其他社会信息。时代湮远,古今隔阂,造成了很多疑惑。因此有大量疑难问题,需要通过多方考证才能获得较为清楚的认识。本文将要讨论的是《数》的算题“秏程”(由简0809和简0802编连而成)和“粟为米”(由简2173、简0137和简0650拼缀编连而成),算题内容是关于粮食加工、仓储事务的,有意思的是,它们都涉及非标准的换算比例,值得关注。

一 对算题“秏程”的研究

简文是:

秏程。以生□(实)为法,如法而成一。今有禾,此一石舂之为米七斗,当益禾几可(何)?其得曰:益禾四斗有(又)七分 0809

斗之二┕,为之述(术)曰:取一石者十之而以七为法┕,它秏程如此。 0802

1.字词释义

秏,同“耗”。《广韵·号韵》:“秏,减也。俗作耗。”

程①“程”的注释参照:彭浩先生的电子邮件及邹大海.从出土竹简看中园早期委输算题及其社会背景.湖南大学学报(社会科学版),2010,24(4):5-10.,计量或计量标准。《汉书·东方朔传》:“武帝既招英俊,程其器能,用之如不及。”颜师古注:“程,谓量计之也。”秦国至汉代的政府为某些部门和工作制定的数量标准,纳入法律的范围,称为程。亦用如动词,表示按程来考虑,例如:张家山汉简《算数书》简70的“程竹”,简87的“程它物如此”,简88的“程禾”。益,增加。《算数书》、《九章算术》多次用“益”。《九章算术》正负术:“异名相益”,益训加。《广雅·释诂二》:“益,加也。”从“贯”,简文将“毌”写作“尹”或者“君”,在《数》中“实”字也有几处写为“ ”。

石,在政府仓储部门中根据不同的粮食种类采用不同的体积标准。例如禾黍(粟)一石为16斗,稻禾一石为20斗,菽、荅、麻、麦一石都是 15斗,粝、粺、毇、粲米一石都是10斗。本条中“此一石”系针对禾一石即16斗而言。①关于“石”的标准参见以下原始文献《:睡虎地秦墓竹简·仓律》之简“仓四一、仓四二、仓四三”(睡虎地秦墓竹简整理小組.睡虎地秦墓竹简.北京:文物出版社,1990,释文注释第二九和三〇页)张家山汉简《算数书》“程禾”条《、九章算术》粟米章《、说文解字》中有关粮米的字条,以及邹大海先生和彭浩先生的校释与考证。彭浩.睡虎地秦墓竹简《仓律》校读(一则).北京大学考古文博学院编.考古学研究(六):庆祝高明先生八十寿辰暨从事考古研究五十年论文集.北京:科学出版社,2006.499-502邹大海.从《算数书》和秦简看上古粮米的比率.自然科学史研究,2003,(4):318-328邹大海.出土《算数书》校释一则.东南文化.2004,(2):83-85(作者称此刊印本有大量编印错误,正确版本见:简帛研究网,http://www.jianbo.org/admin3/html/zhoudahai02.htm,2004-4-11)邹大海.关于《算数书》、秦律和上古粮米计量单位的几个问题.内蒙古师范大学学报(自然科学汉文版),2009,38(5):508-515.。

2.算法分析

术文的算法相当于:

这是不完整的,实际计算中应包含这样的计算步骤:

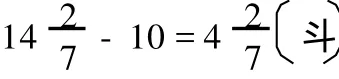
邹大海先生认为这个计算方法不符合原题②邹大海先生对算题“秏程”的意见引自邹大海先生于2010年8月22日的电子邮件.。由10斗禾舂出7斗米,出米率就远高于由粟舂出粝米的比例16∶10=10∶6,与“耗”这一题设不符。此题应理解为:正常情况下1石(即16斗)禾(粟)舂 1 石(即 10 斗)米 ,现在由于有损耗,所以1石禾只舂出7斗米,那么要得到正常舂出的1石米,应该增加多少损耗的禾。先计算是在有损耗的情况下,要获得正常舂出的一石米所需要的禾的数量,再从中减去,便是“当益禾”的数量,算出来是斗,这与原简答案不合。如果原题没抄错,则可能为设题者搞错了,或者在流传过程中被改错了。

二 对算题“粟为米”的研究

简文是:

粟一石为米八斗二升,问米一石为粟几可(何)?曰:廿斗 2173

百廿三分斗卌为米一石,术曰:求粟 0137

1.简的编连和复原方案

从现存简文看,算题无题名,根据内容暂题为“粟为米”。

简0650完整,参照“日本中国古算书研究会”的意见③日本“中国古算书研究会”对简0650的编连意见参照大川俊隆先生于2010年8月19日电子邮件.,将简0650编连入此算题。简2173与简0137可拼缀,断口契合,内容连贯。拼缀后简长度是21.0cm,简上下仍残。《数》的完整简全长多为27.5cm左右,上编绳下缘距离简首多为1.5cm左右,下编绳上缘距离简尾约1.8cm左右,整简字数多在38～45字之间。下面拼缀复原简2173和简0137。

邹大海先生的意见是④邹大海先生对简2173和简0137的复原意见参照邹大海先生于2010年8月23日的电子邮件转述.:从照片看“粟一石”三字已残缺大部分,宜先作缺字,再加注说明当作“粟一石”。简2173在“粟一石”之前残断,也不排除残断部分还有未知文字的可能性。在简0137下段补出“以八斗二升”是符合题意的。“求粟”和“以八斗二升”之间按照《数》算题的习惯表述可补“之法”,“之术”,“者”等。邹先生提出六种复原方案:

第一种可能:简2173“粟一石”前补“禀”字,简 0137后补“者,以八斗二升”字,这时字距较稀了一点。

第二种可能:前简仍补“禀”字,后简补“也者,以八斗二升”。

第三种可能,前者补“禀”,后简补“之法,以八斗二升”。

第四种可能:后简补“为米者,以八斗二升”。

第五种可能:后简补“为米一石者,以八斗二升”,这时文字会比较密。

第六种可能:比第五种还多补一个字:“之为米一石者,以八斗二升”。

总之,什么情况都有可能,很难判断哪一种有明显的优势。但简0137末尾与简0650相连的文字补作“以八斗二升”是不错的。

2.算法分析

我对此题原来的理解是:“禾粟一石为粟谷八斗二升,问粝米一石为禾粟几何。隐含已知条件“粟率五十,粝米三十”。算式是:

日本“中国古算书研究会”对此题的解释是⑤日本“中国古算书研究会”对算题“粟为米”的意见参照大川俊隆先生于2010年8月至9月的电子邮件转述.:

本题和《算數书》的“舂粟”题一致。题中“粟一石”是指重量一石,对应容量50/3斗。本来从容量50/3斗的粟中能取得10斗的米,现在因损耗只取得8斗2升的米。问若要取得米1石(10斗)需多少粟。比例式是粟50/3斗:米8斗2升=粟 X:米10斗。

邹大海先生对此算题做了详细解析,他的意见主要有下面几点①邹大海先生对算题“粟为米”的意见参照邹大海先生于2010年8月20日至8月23日的电子邮件转述.:

(1)将《数》的这个算题跟《算数书》的“舂粟”题比较,这两个问题有一致性,《数》的这个问题可以用损耗来解释,但其文本本身和算法本身都未及此。

(说明:以上图片均为截取的片段。图片并列照片和红外线扫描片。复原方案所补出的图形、文字均采自《数》竹简。)

《算数书》舂粟题,涉及了在标准情况下舂粟时粟和米的数量关系和在有损耗情况下舂粟的数量关系,要求的是在有损耗情况得到一石米时所需要补足的供损耗的粟。其计算过程中,都在术文之外还需要另外计算术文中的参数。而《数》的这个问题,不涉及损耗问题,其术文如果把简0137损失文字补上“以八斗二升”(或类似文字)后,则术文提供的算法是完整的。从另一个角度看,虽然从舂粟的标准比例来说,《数》这个问题中一石粟只得八斗二升米,可以用存在损耗来理解,但不管一石粟舂出的米是八斗二升,还是别的什么数量,只要按正比例关系依术计算出结果来,跟损耗不损耗没有关系。

(2)《算数书》“舂粟”条中“当益秏粟几何”前,应脱落了表示已知得到一石米这样一个已知条件的文字,从秦简《数》看,这个意见是有根据的,并非古人有这种省略的习惯。但是因为在简0809“今有禾,此一石舂之为米七斗,当益禾几可(何)?”中,也没有表示已知舂出一石米这个条件的文字,所以《算数书》中“舂粟”省去表示这个条件的文字也是可能的。不过,既然《数》简0809的这个题术文不全,答案很可能不对,所以题设被抄错或改错的可能性也不小,因此也不能由此认定《数》和《算数书》中表示已知得到一石米的文字没有出现,一定是一种省略的方式,而不可能是流传错误。

(3)秦简《数》这个问题的方式为:在政府的仓储事务中,由粟舂出的米(粝米)按通常的体积计量方式以十斗为一石,粟则按舂出一石米所需要的粟的体积即十六斗大半斗为一石。因此,如果假设秦简《数》的这个问题以政府的仓储事务为现实背景,那么简2173和简0137中“粟一石”就是粟十六斗大半斗,“米一石”即“米十斗”。因此3支简连在一起形成的整个问题就是:

[已知]粟一石(十六斗大半斗)能得到米八斗二升,问要得到一石(十斗)米相应需要多少粟?[答]曰:[粟]廿斗又一百廿三分斗之卌能得到一石(十斗)米。术曰:要求粟[之得一石米者],[以八斗二升]为除数(法),以(一石米的斗数)十斗乘粟(一石的斗数)十六斗大半斗为被除数(实),被除数中有与除数相同的部分就得到一斗(实如法得粟一斗)(或者说被除数除以除数)。

上面方括号内的文字,是为使文意清楚而补足的,圆括号内的文字是解释性的说明文字。

这个根据现代读者阅读习惯对问题做的尽量贴近原文的重写,并不涉及粟米比率5∶3,也不涉及损耗数和损耗率。术文列成算式就是:

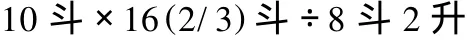
这两个问题,反映了政府部门除采用标准的禾(粟)、米换算比例外,还根据实际情况(如粮食的成色、保存的状况等),用数学方法解决非标准比例状态下的问题。

H ao Cheng and Su Wei Mi,two Problems in the Unearthed Book Shu

XIAO Can1,2

(1.Department of Architecture,Hunan University,Changsha 410082;2.Yuelu Academy,Hunan University,Changsha 410082)

This article gives detailed descriptions of two problems in the Mathematical text,S hu(数,Numbers and Reckoning)written on the Bamboo Strips owned by the Yuelu Academy.One problem is“Hao Cheng”(norm for wastage)and the other is“Su Wei Mi”(the exchange of millet and husked millet).The two problems provide information on millet grain processing,storing and other production activities and the concerning regulations.They also validate the opinion that the measurement unitS hihad its particularity in Early China.

“Hao Cheng”(norm for wastage),“Su Wei Mi”(the exchange of millet and husked millet),the unearthed bookS hu(numbers and reckoning),Bamboo Strips of Qin Dynasty owned by Yuelu A-cademy

K877.5

A

1008—1763(2011)02—0009—03

2010-12-16

国家社会科学基金项目《岳麓书院藏秦简的整理与研究》(09BZS001)

肖 灿(1976—),女,湖南湘潭人,湖南大学岳麓书院博士,建筑学院讲师.研究方向:中国文化史.