一类创新型权证的数学模型
2011-12-20任学敏
刘 易,任学敏
(同济大学 应用数学系,上海200092)
2004年2月,国务院颁布了《国九条》,明确提出了股改的要求.股权分置改革是非流通股股东通过向流通股股东提供一定的对价作为补偿,使非流通股获得流通权,实现同股同价.
通常,非流通股股东用送股和认购或认沽权证的方式来支付对价,但也有上市公司(如上海医药和农产品)送创新型权证,该创新型权证不同于一般权证的是它将股票和权证相捆绑,承诺流通股股东在一定时间后有权按约定的价格将股票出售给非流通股股东,这相当于在流通股股票里嵌入了认沽权证,从而股价将不再呈现几何布朗运动.由于一般的权证定价都是假设股价服从几何布朗运动,因此不能简单地从股票价格出发来计算该创新型权证的价格.为了解决这个问题,借鉴信用风险定价理论中的结构化方法.结构化方法由Merton[1-2]最先提出,是以公司资产为状态变量,到期日资不抵债为破产的标准,利用期权定价理论[3],对信用风险进行度量的方法,Black和Cox[4]提出了首次通过模型,将模型推广到可在到期日之间发生违约的情况.本文以公司资产作为基本变量,采用首次通过模型,运用无套利原理建立数学模型,对有担保和无担保的情况进行分析,得出该创新型权证的定价公式.最后对不同市场变量对创新型权证价格的影响作了理论和数值分析.
1 数学模型
1.1 基本假设
(1)公司负债为F,公司资产为V,公司负债到期日为T1;其中,F,V是相对每份股票而言的,且由于在零时刻公司资产V0应该不能小于负债F,有V0≥F>0;公司非流通股m份,流通股n份.
(2)对于公司资产Vt,假设其服从几何布朗运动:

式中:μ,σ为常数,分别表示公司资产的期望回报率和波动率;dWt为标准布朗运动,即:

(3)创新型权证的价值为S(Vt,t),其到期日T≥T1,敲定价即流通股股东有权出售的股票价格为K.
(4)市场不存在套利机会,无风险利率为常数r>0;股票无股息;无交易费和税收.
1.2 建立方程
利用Δ-对冲原理[5],在时间段(t,t+dt)上构造投资组合Π,使其在(t,t+dt)时间段内无风险,Π 是由1份创新型权证S和Δ份公司资产V组成,即:

由伊藤公式,组合在(t,t+dt)时间的收益是:


即:

由式(3),(5),可得:

1.3 有担保和无担保时的定解条件与求解
1.3.1 定解条件
当该创新型权证有担保且不考虑担保公司违约的情况下,如果公司资产V减去负债在权证到期日T的贴现Fe-r(T1-T)大于或等于敲定价K,在到期日T,该创新型权证的价格S就是V-Fe-r(T1-T);否则,由于有担保,在不考虑担保方违约的情况下,在到期日,T该创新型权证的价格S都等于敲定价K.因此定解问题为
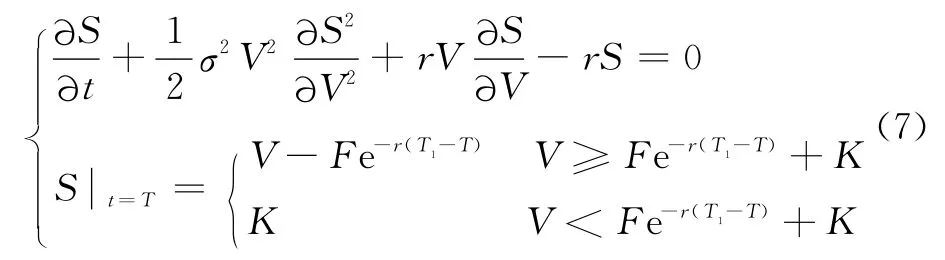
当该创新型权证无担保且V-Fe-r(T1-T)≥K时,在到期日T该创新型权证的价格S即为V-Fe-r(T1-T);否则,由于无担保,则需做进一步的讨论:如果将公司资产V减去负债在权证到期日T的贴现Fe-r(T1-T),即V-Fe-r(T1-T)这一部分全部给流通股股东,则对于流通股股东而言即可以获得,如果V-Fe-r(T1-T)≥K,则在到期日T该创新型权证的价格S等于敲定价K;如果0≤V-Fe-r(T1-T)≤K(即公司资产大于负债,公司未破产),则在到期日T该创新型权证的价格S就等于;如果其值小于0(即公司资产小于负债,公司破产),则在到期日T该创新型权证的价格S等于0.因此定解问题为

1.3.2 求解方程
作自变量代换,

方程(6)可化为常系数抛物型方程

则定解问题(7)转化为常系数抛物型方程的初值问题

其中,

同样的,定解问题(8)也可转化为常系数抛物型方程的 初值问题

作函数变换,

初值问题(11)变为
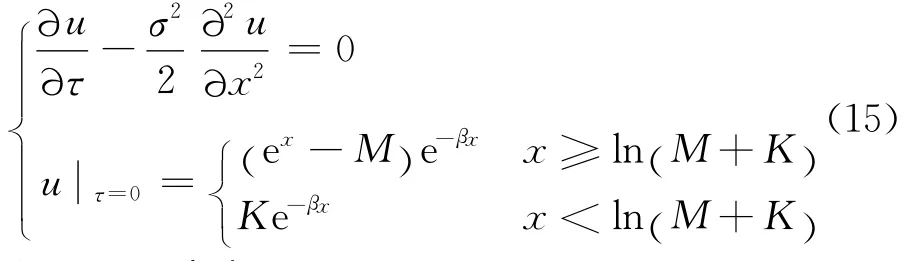
初值问题(13)变为

根据Poisson公式[6]
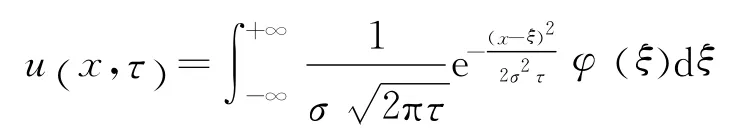
其中,φ(ξ)为初值.
则初值问题(15)的解为

由此可得
定理1 在有担保情况下,创新型权证的定价
公式:

其中,
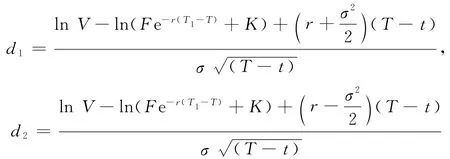
对无担保的情况:

从而有:

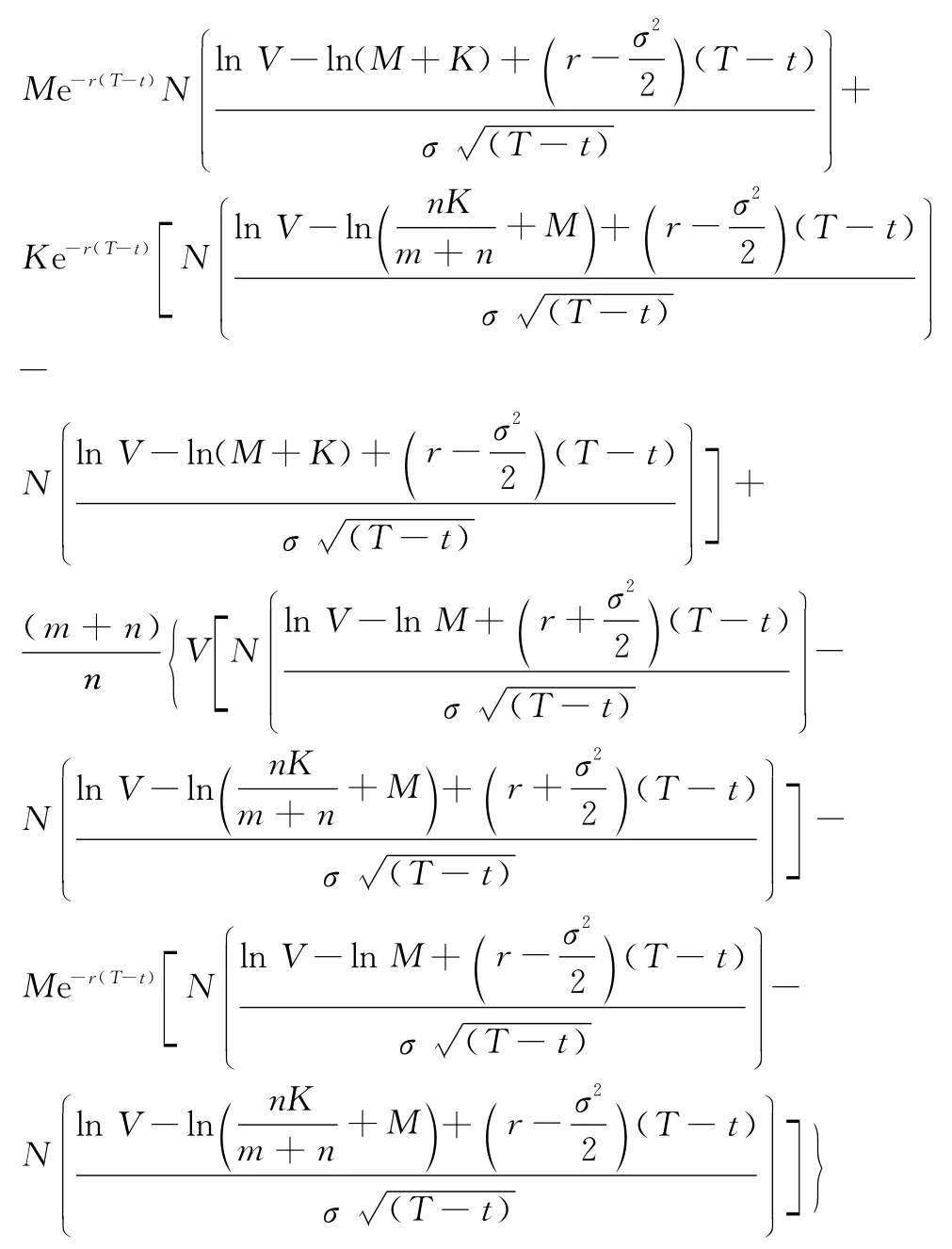
定理2 在无担保情况下,创新性权证的定价公式:

其中:
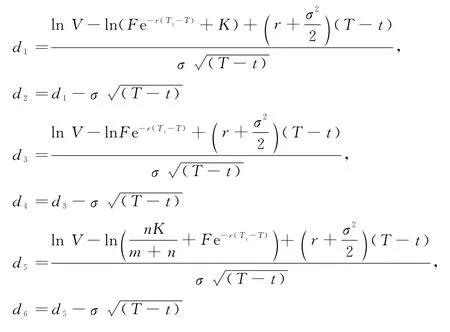
2 创新型权证S 与各变量之间的关系
2.1 波功率σ 与S 的关系
图1为σ与S的关系图,图中,取V=10,F=2,K=5,T1=1.1,T=1,r=0.1,m=5,n=5.

图1 创新性权证价格与波动率的关系Fig.1 Relationship between innovative warrant price and volatility
由图1可知,创新型权证的价格在不同情况下有所差异,由高到低分别为有担保情况和无担保情况.这是因为无担保情况相对于有担保情况在公司破产时可能的获利要小.同时,在有担保和无担保的情况下,创新型权证的价格均随波动率的增大而增大.这是因为波动率的增加对其价格有两方面影响:其一是增加了在到期日公司破产的可能性;其二是增加了到期日获利的可能性,但由于有非流通股东提供的保底因素,后者的影响起主导作用,因此创新型权证的价格随波动率的增大而增大.

图2 极端情况下权证价格与波动率的关系Fig.2 Relationship between innovative warrant price and volatility in extreme case
由图2可知,这里考虑在极端情况下,即公司的资产大多来自于负债,这会造成破产可能性增大,价格的变化与图1相似,但是由于破产的可能性增大而降低了权证的价格.
2.2 公司负债F 与S 的关系
取V=10,σ=1,K=5,T1=1.1,T=1,t=0,r=0.1,m=5,n=5(图3).
创新性权证的价格在不同情况下有所差异,由高到低分别是有担保情况和无担保情况.这是因为,无担保情况相对于有担保情况在公司破产的情况下可能的获利要小.

图3 创新性权证价格与公司负债的关系Fig.3 Relationship between innovative warrant price and company’s debt
同时可以看出,在有担保和无担保的情况下,创新性权证的价格均随公司负债的增大而增大.这是因为负债的增大增加了公司破产的可能性,从而减少了可能的获利.
2.3 m/n与S 的关系
取V=10,σ=1,F=2,K=5,T1=1.1,T=1,t=0,r=0.1,m=5,n=5(图4).

图4 创新性权证价格和非流通股与流通股股东股份的比值的关系Fig.4 Relationship between innovative warrant price and ratio of non-tradable and tradable share
由图4可知,在无担保的情况下,创新型权证的价格随公司非流通股股东和流通股股东所占股份的比值的增大而增大.这是因为比值的增大增加了非流通股股东在破产时给流通股股东的补偿.
2.4 敲定价K 与S 的关系
取V=10,σ=1,F=2,T1=1.1,T=1,t=0,r=0.1,m=5,n=5(图5).
由图5可知,无担保情况相对于有担保情况在公司破产的情况下可能的获利要小.同时在有担保和无担保的情况下,创新型权证的价格均随其敲定价的增大而增大.这是因为敲定价的增大增加了可能的获利.

图5 创新性权证价格与敲定价的关系Fig.5 Relationship between innovative warrant price and strike price
2.5 无风险利率r与S 的关系

图6 创新性权证价格与利率的关系Fig.6 Relationship between innovative warrant and interest rate
由图6可知,在有担保的情况下,创新型权证的价格随利率的增大先减后增;在无担保的情况下,创新型权证的价格随利率的增大而增大.这是因为利率对其价格有两方面影响:其一是利率的增加降低了在到期日的负债,增加了可能的获利;其二是利率的增加减少了敲定价在初始时刻的现值.在有担保的情况下,先受后者的影响更大,表现为其价格随利率的增大而减小;随着利率的进一步增大,前者的影响超过后者,表现为其价格随利率的增大而增大.在无担保的情况下,由于更多考虑破产的影响,前者对利率的影响始终占据主导地位,表现为其价格始终随利率的增大而增大.
2.6 公司负债到期日T 与S 的关系
取V=10,σ=1,F=8,K=5,T1=1.1,t=0,r=0.1,m=5,n=5(图7).
由图7可知,在有担保和无担保的情况下,创新型权证的价格均随其到期日的增大而增大.这是因为到期日对其价格有两方面影响:其一是到期日的增大增加了可能的获利;其二是到期日的增大而增大了破产的可能性.同样由于非流通股股东提供的保底,前者的影响起主导作用,表现为其价格随到期日的增大而增大.

图7 创新性权证价格与权证到期日的关系Fig.7 Relationship between innovative warrant and maturity date
[1] Merton R.On the pricing of corporate debt:the risk structure of interest rates[J].Journal of Finance,1974,29:449.
[2] Merton R C.Option pricing when the underlying stock returns are discontinuous[J].J Polit Econ,1976,5:125.
[3] Black F,Scholes M.The pricing of options and corporate liabilities[J].Journal of Political Economy,1973,81:637.
[4] Black F,Cox J C.Valuing corporate securities:some effects of bond indenture provisions [J].Journal of Finance,1976,31:351.
[5] 姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社,2003.74-89.JIANG Lishang.The mathematical models and methods in option pricing[M].Beijing:Higher Education Press,2003.74-89.
[6] 姜礼尚,孙和生,陈志浩,等.偏微分方程选讲[M].北京:高等教育出版社,1997.37-48.JIANG Lishang,SUN Hesheng,CHEN Zhihao,et al.Some topics on partial differential equation[M].Beijing:Higher Education Press,1997.37-48.
