基于相关机会目标规划的钢板切割分配建模

张永全,徐克林,孙 禹

(同济大学 机械工程学院, 上海201804)

造船业是一个国家经济和技术实力的重要体现.近年来,我国造船业发展迅速,2008 年,全国造船产量已达2 .881 ×107载重吨, 占全球市场份额29 .5 %,居世界第3 位[1].但是, 我国造船效率与国际先进船厂相差巨大,骨干船厂生产效率只有日本、韩国的1/3～1/4[2].因此, 我国要成为造船强国, 必须提高造船效率.

目前, 造船业竞争的焦点已由规模转向核心竞争力.钢板切割是船厂的核心竞争力之一, 也是影响造船效率的一个重要因素.为了提高钢板的利用率,国内外对钢板排样、套料进行了深入的研究[3-6],分析了利用率和规格之间的关系[7];为了提高切割效率,对划线、切割路径等进行了优化[4,8-9],将成组技术与调度规则结合起来[10];为了实现准时制生产,采用多目标柔性作业车间调度技术实现多机工作负荷分配[11-12].然而, 对于供给不确定情况下如何在不同的切割机上分配待切割的钢板的研究较少.本文假设在钢板排样、划线、切割路径等都已经确定情况下,利用相关机会目标规划对多个不确定钢板供给端向多个数控切割机分配切割任务, 以满足生产的有序性和多目标要求.

1 钢板切割的供给-分配系统

某船厂预处理后的钢板主要通过3 种途径供给4 台不同的数控切割机(CNC)进行切割:①地面堆放;②平板车存放;③临时抽板, 其供给与分配情况如图1 所示, 图中,x1～x4 分别为平板车存放供给CNC1～CNC4 的钢板量;x5～x8分别为地面堆放供给CNC1～CNC4 的钢板量;x9和x10分别为临时抽板供给CNC3 和CNC4 的钢板量.按照生产计划,在班前将每天要切割的钢板放置于地面和平板车上,如果出现生产遗漏、设计变更等需要补料和插单情况,则按临时抽板处理, 并在班后统计3 种供给量.受钢板厚度、前道工序及生产准备影响,这3 种供给量每天都是不确定的, 无法准确按照生产要求顺序供给和逆序码放.因此,该钢板切割供给-分配系统是一种典型的随机任务分配问题.

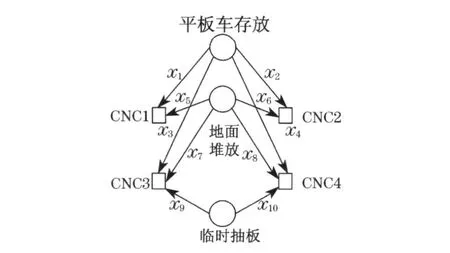
图1 钢板切割的供给-分配示意Fig .1 Supply-distribution illustration of steel plate cutting

由于钢板切割过程中大量的并行作业彼此穿插、相互影响,人员、设备、物料投入密集, 复杂程度高、控制难度大[1],作业时间变动范围广, 无法在较低成本下精确按照多目标柔性作业调度方案进行切割任务分配, 只能根据作业人员的经验向数控切割机分配钢板.而人为分配具有很大的随机性, 经常造成关键设备利用率不高及生产混乱情况, 同时, 这种随机性还会造成钢板搬运任务增加, 场地占用长久等, 使物流成本升高, 甚至会造成钢板积压、生产不畅、交货延迟等现象,降低了船厂的竞争力.通常认为造成这种现象的源头在于钢板供给端的不确定性, 是不能控制和消除的, 以至于严控临时抽板量.因此, 必须寻求一种介于完全随机分配和多目标柔性精确分配之间的分配策略, 在维持生产有序进行状态下挖掘切割潜力, 满足生产的多目标要求.

2 相关机会目标规划

2.1 求解随机任务分配问题的方法

通常情况下, 求解随机任务分配问题的方法有3 种[13].

(1)从期望值的角度出发, 用函数的期望值分别代替原来目标函数和约束条件中的不确定函数,建立期望值模型.

(2)从机会测度的角度出发,由于必须在观测到约束条件中的随机变量实现之前决策,故允许决策在一定程度上不满足约束条件, 只要求其机会测度不小于给定的置信水平, 建立机会约束规划模型[14].

(3)从极大化事件实现的机会出发, LIU 提出了相关机会规划理论[15].该理论用不确定环境取代可行集,使事件的机会函数在不确定环境下达到最优,即极大化随机事件成立的机会[16].

在期望值模型和机会约束规划中, 对实际问题建模后,其可行集本质上已经确定, 但有时给出的最优解在现实中可能无法执行.相关机会规划并不假定可行集是确定的, 虽然它也给出一个确定的解, 但只是要求该解在实际问题中尽可能地被执行[13].

2 .2 相关机会目标规划模型

在钢板切割的供给-分配系统中, 许多目标是互斥的, 决策者会根据其重要性为这些目标建立一个优先结构.相关机会目标规划就是在给定的优先结构下极小化各目标函数与目标值的偏差(正偏差或负偏差).在随机任务分配问题的通用模型[13]中,对于同一优先级下的多个目标偏差的处理采用(·)形式,其中n表示系统目标的个数,(·)表示偏差求和.在该模型中, 对于任一优先级, 系统目标的偏差和被计算1 次.当存在多个优先级时, 目标的偏差和被重复计算了, 否则需要定义大量的偏差零权重因子, 使模型复杂性增大.针对这一问题, 本文对其同一优先级下多目标的处理过程进行了修正.对于含有s个优先级、t个目标、m个随机约束的决策系统,修正的相关机会目标规划模型为

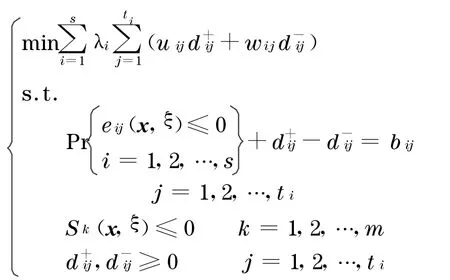
式中:s为优先级的数目;λi为优先级因子, 表示各个目标的相对重要程度, 且对于∀i,λi≫λi+1;t i为第i个优先级中的目标数目,且为对应于优先级i的第j个目标正偏差的权重因子;w ij为对应于优先级i的第j个目标负偏差的权重因子;e ij(x , ξ)≤0 ,i=1 ,2 , …,s,j=1 ,2 , …,t i为第i个优先级中的第j个目标事件,设为E ij, x 为决策向量, ξ为随机向量, Pr{eij(x , ξ)≤0 ,i=1 ,2 , …,s,j=1 , 2 , …,t i}表示事件E ij的概率测度;b ij为第i个优先级中的第j个目标事件的目标值;d+ij为第i个优先级中的第j个目标偏离目标值bij的正偏差,且设f ij(x)=Pr{e ij(x ,ξ)≤0 ,i=1 ,2 , …,s,j=1 ,2 , …,t i}为事件E ij的机会函数, 即d+ij=;d-ij为第i个优先级中的第j个目标偏离目标值b ij的负偏差, 即d-ij=;随机约束S k(x , ξ)≤0 ,k=1 ,2 , …,m为系统约束中的不确定环境.

在相关机会目标规划模型中, 虽然决策向量x不是随机向量, 但是具有一些不确定性质.它主要由2 个因素确定,一个来自于随机变量ξ的实现,另一个来自于实际系统给定的约束.

3 模型求解

在通常情况下, 相关机会目标规划模型都很复杂,多采用人工智能方法进行求解.这里采用融合随机模拟、BP 神经网络(error back propagation neural network)和遗传算法的混合智能算法进行求解, 流程如图2 所示.

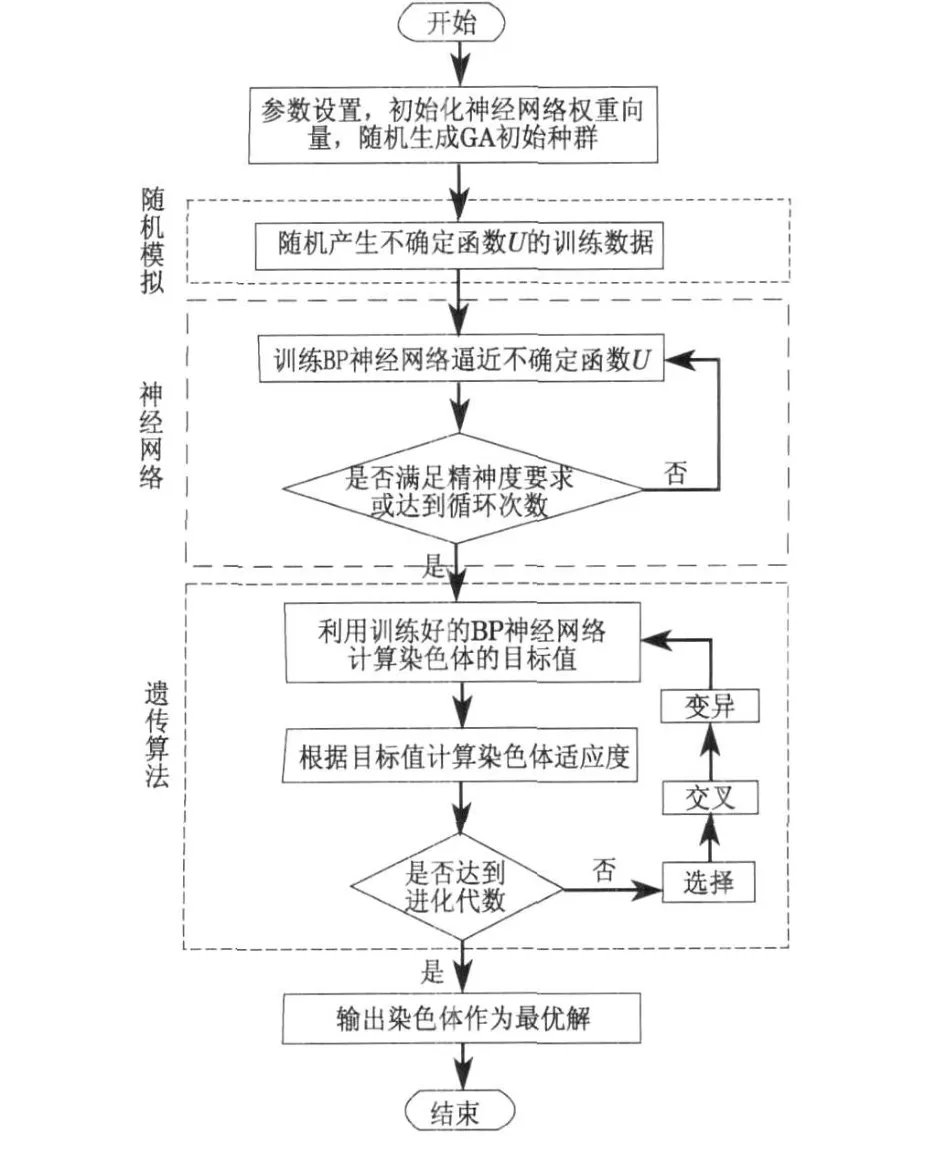
图2 混合智能算法流程Fig .2 Flow chart of hybrid intelligent algorithm

3.1 随机模拟环节

在相关机会目标规划模型中, 设在不确定环境Sk(x,ξ)≤0 ,k=1,2,…,m下 有t个 事 件e ij(x ,ξ)≤0 ,i=1,2,…,s,j=1 ,2,…,t i,根据不确定原理,该事件的机会等于此事件相容的概率[13],可得事件E ij的机会函数为

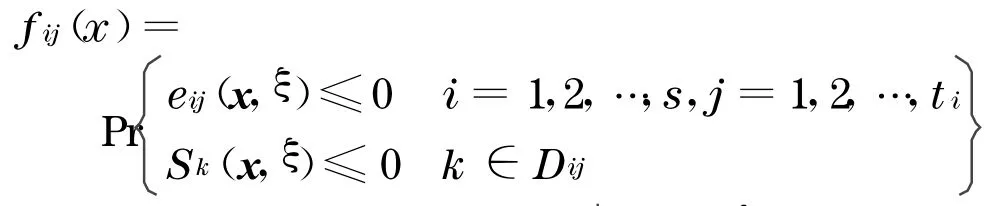
在混合智能算法中, 首先利用随机模拟为不确定函数

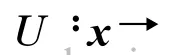
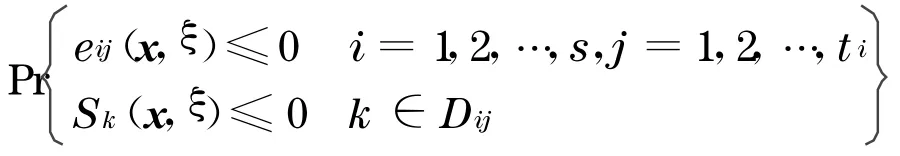
产生训练数据.根据Chebyshev 弱大数定律,结合事件E ij本身的实值函数,随机产生事件E ij的相关支撑E**ij的向量x′与随机向量ξ′,并记录不等式S k(x′,ξ′)≤0 成立的次数N′.当随机模拟次数为N时,用N′/N作为事件E ij的机会函数值,即f ij(x)=N′/N并作为BP神经网络的一个训练数据.

3.2 神经网络环节

在混合智能算法中, 经过随机模拟产生不确定函数U的多组训练数据进入神经网络环节进行训练,如图2 所示.设E*为所有事件Eij的支撑E*ij的并集, α为E*中独立变量的数目,β 为包含概率测度的事件的数目.采用单隐含层BP 神经网络来逼近不确定函数U,并以E*中独立变量作为输入神经元,以事件的概率测度作为输出神经元, 则隐含层神经元数目γ可根据经验公式获得:

在此BP 神经网络中,设训练数据为f k(x), 训练输出为F k(x), 通过训练寻找权重向量来极小化误差函数其中,n为训练次数.若此误差函数值小于预先设定的精度ε0且满足训练次数,则保存此BP 神经网络的权重向量,混合智能算法进入遗传算法环节, 否则继续训练.

3.3 遗传算法环节

在本环节中, 直接采用浮点向量作为染色体解向量.将经过训练的BP 神经网络用来计算染色体的目标值,并使用基于序的评价函数e(Vi)计算每个染色体V i的适应度,即e(Vi)=ρ(1-ρ)i-1,ρ为序参数,ρ∈(0 ,1),i=1 ,2,…,p(p为种群大小).

对于未达到进化代数的染色体,通过选择、交叉和变异后重新计算染色体的目标值.首先, 通过轮盘赌方式选择染色体,然后以概率Pc进行线性交叉以取代其父代.即对于选中的2 个父代染色体Vi和V j来说,经过交叉操作产生子代染色体V′i和V′j,V′i=ωV i+(1-ω)V j,V′j=(1-ω)V i+ωV j,i,j=1 ,2,…,p,其中, ω为随机数, 且0 ＜ω＜1 .最后以概率P m进行变异以取代原染色体, 即对于染色体V i,根据目标实值定义一个较大的数θ和变异方向τ,使得变异后染色体V′i满足V′i=V i+θτ,i=1 ,2,…,p,其中, τ为随机数,且-1 ＜τ＜1 .为保证所有产生染色体的合法性, 在选择、交叉和变异环节嵌套约束检查模块.经选择、交叉和变异后得到新种群可进入下一代进化, 直至达到进化代数,并输出最优染色体作为该相关机会目标规划模型的最优解.

3.4 最优解的执行

在期望值模型和机会约束规划中, 当求得问题最优解x*后, 可以分别执行或同时执行x*的每一个分量,对结果无影响.而在相关机会目标规划中,可行集是随机的, 解向量的各个分量中存在等级结构.因此, 在执行最优解的各个分量时, 必须严格按照目标结构, 依次执行各优先级目标对应事件的支撑,满足级别高的分量优于级别低的分量.

4 应用实例与分析

某船厂切割车间钢板供给-分配系统如图1,通过平板车存放、地面堆放和临时抽板3 种途径对4 台数控切割机分配钢板.CNC1 和CNC2 为新购设备, 切割效率高;CNC3 和CNC4 为旧设备, 切割效率较低.如遇补料和插单, 需中断原切割计划, 并以临时抽板方式供给CNC3 和CNC4 .为防止钢板堆积过多而变形,平板车和地面堆放钢板数量有限制;而临时抽板属实时运送, 无此限制.受钢板厚度、前道工序、生产准备影响,这3 种供给量每天都是随机的.

考虑到钢板厚度等的差异, 该船厂对钢板切割长度 进 行 了 如 下 换 算:lC =lA αT +lBαM+(l′A +l′B)αE,其中,lC为钢板切割长度;lA为数控切割长度;αT为厚度系数;lB为数控划线长度;αM为划线长度系数;l′A为切割空程长度;l′B为划线空程长度;αE为空程长度系数.

考虑到设备性能, 该船厂对4 台数控切割机预设了最大切割长度和完成最大切割长度的目标概率,如表1 所示.计算方便起见,采用千米为单位.

表1 最大切割长度和目标概率Tab.1 Each supreme cutting length and corresponding target probability

由于CNC1 切割效率最高, 对生产影响较大,优先级最高;CNC2 切割效率次之, 优先级较高;CNC3和CNC4 切割效率较低, 优先级一般.在生产中, 希望极大化它们完成最大切割长度的机会.对于临时抽板, 由于担心会造成生产混乱, 希望极小化其供应量,但是优先级最低.为了合理地从3 个不确定供给端向4 台数控切割机分配钢板, 对该钢板切割供给-分配系统建立的相关机会目标规划模型如下:

其中,lexmin表示按字典序极小化目标向量;d+1～d+4,d-1～d-4分别表示4 台数控切割机偏离切割目标的正、负偏差;d+5,d-5分别表示临时抽板数量偏离目标零的正、负偏差;随机变量ξ1,ξ2,ξ3分别表示3 种途径的日供给量,该船厂统计资料显示, ξ1,ξ2,ξ3分别近似服从正态分布N1(2 .095 755, 0 .642 8362),N2(3 .185 918 ,0 .802 7962)和N3(0 .115 436 ,0.087 1932).

对该钢板切割供给-分配系统的相关机会目标规划模型运用混合智能算法求解.首先, 随机模拟6 000代为不确定函数U产生训练样本, 然后采用3 000个样本训练BP 神经网络(6 个输入神经元,12 个隐含层神经元,4 个输出神经元)来逼近不确定函数U,最后采用遗传算法进行求解.在遗传算法中,种群数p=35 ,交叉概率Pc=0 .32 ,变异概率Pm=0 .23 ,基于序的评价函数参数ρ=0 .05,遗传迭代3 000次.通过执行该混合智能算法,得到最优解

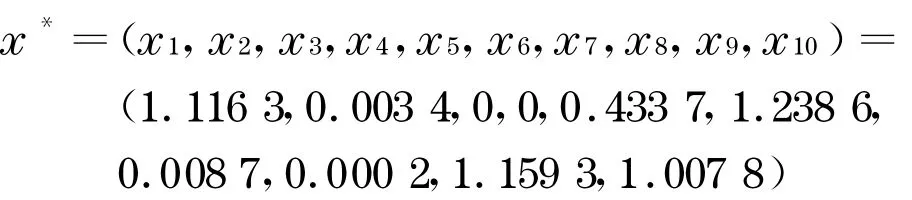
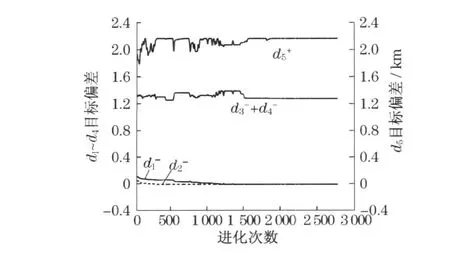
图3 各目标分量进化过程Fig .3 Evolution of each target component

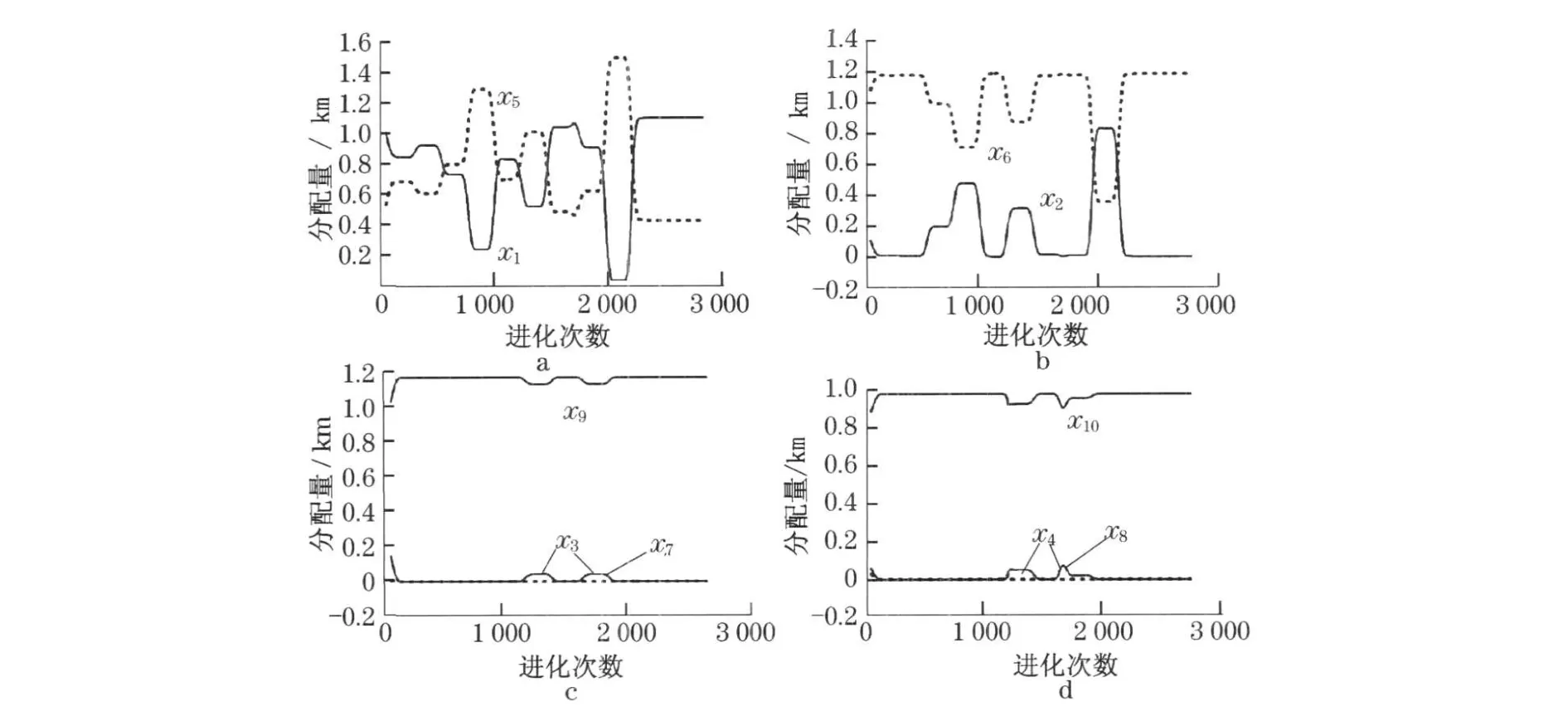
图4 各决策分量进化过程Fig .4 Evolution of each decision-making component

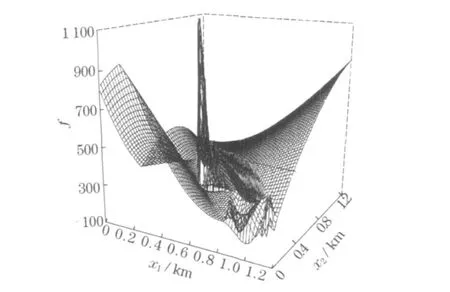
图5 f 与x 1,x 2 的变化关系Fig .5 Relationship among f,x 1 and x 2

在最优解x*中,决策分量x3=x4=0,x7≈x8≈0 ,说明系统几乎未从平板车和地面堆放处向CNC3 和CNC4分配钢板.由于平板车距离CNC3 和CNC4 较远,这种分配可以降低电磁吊的行走距离, 减少浪费.x1,x2,x5,x6数值较大,说明系统向CNC1 和CNC2 供给钢板数量较多.由于彼此间距离很近,减少了搬运作业工作量从而降低了物流成本.

在对应最优解x*的目标向量中, 分量,说明CNC1 和CNC2 完成最大切割长度的概率可以达到目标值,即保证了关键设备的利用率.CNC3 和CNC4 完成最大切割长度的机会仅有2 .75 %(即(0 .69-0 .662 5)×100 %)和2 .61 %(即(0 .65-0 .623 9)×100 %),其切割潜力提升空间较大.此时, 临时抽板量为2 .167 1 km,数量较大, 已经不局限于补料和插单.地面堆放、平板车存放及临时抽板供给量的随机性对切割任务分配的影响也通过模型得到控制和消除.

由于CNC4 切割能力较小、负荷较轻,可以考虑撤去, 用来存放部分“临时抽板”, 加大供给量, 极大化CNC1～CNC3 完成最大切割长度的机会,增强钢板切割供给的稳定性,且为进一步提升3 台数控切割机的性能做准备.同时,由于现有的切割机加工坡口效率较低,也可考虑将原CNC4 所占空间专门用来加工坡口,降低CNC1～CNC3 作业难度,缩短切割周期,提高作业效率,有利于船厂竞争力的增强和素质的全面提升.

总之,通过对该钢板切割供给-分配系统进行相关机会目标规划建模和求解, 基本满足了生产的多目标要求, 而供给端的不确定性对生产造成的影响也通过运用相关机会目标规划加以控制和消除,不会造成生产混乱.

5 结语

针对钢板切割供给-分配系统中多个供给端的不确定性, 应用相关机会目标规划对该系统进行建模, 证实由于供给的不确定性对生产系统造成的影响可以控制和消除, 极大化关键设备完成最大切割长度的机会, 减少了浪费, 实现了切割的多目标要求.根据求解结果提出加大临时抽板量的同时维持生产的稳定性.最后结合生产实际分析进一步提高效率的措施以最大程度挖掘切割潜力, 为生产过程存在不确定资源分配问题的类似作业提供参考.

致谢 感谢同济大学经济与管理学院柯华老师的指导.

[1] ZH ANG Y Q,XU K L, ZHO U G S, et al.Simulation and optimization of hull erection based on P-F TPN[C] ∥2009 16th International Conference on Industrial Engineering and Engineering Management. Piscataway : IEEE, 2009:1860-1864.

[2] 金壮龙.推进战略转型建设世界造船强国[EB/ OL] .[2009-02-01] .http:∥www.ccps .gov .cn/ dxrd.php? col =161&file=4839.JIN Zhuanglong .T o build a w orld shipbuilding power by strategy transformation[EB/ OL] .[2009-02-01] .http:∥www.ccps.gov.cn/ dxrd.php? col=161&file =4839.

[3] La Brooy R.Amethod for optimising the nesting of multiple ,hig hly complex shapes using a modified simulated annealing algorithm[J] .International Journal of Systems Science, 2009,40(2):155.

[4] Jang C D,H an Y K .An approach to efficient nesting and cutting path optimization of irregular shapes[J] .Journal of Ship Production,1999, 15(3):129.

[5] Hifi M, Paschos V T ,Zissimopoulos V .A simulated annealing approach for the circular cutting problem [J] .European Journal of Operational Research, 2004, 159(2):430.

[6] Ramesh Babu A,Ramesh Babu N .A generic approach for nesting of 2-D parts in 2-D sheets using genetic and heuristic algorithms[J] .Computer-Aided Design, 2001, 33(12):879.

[7] 赵定刚, 刘建峰, 张志英, 等.提高造船钢材利用率的方法研究[J] .江苏科技大学学报:自然科学版, 2006, 20(6):5.ZH AO Dinggang,LIU Jianfeng,ZHANG Zhiying et al.Study on improving steel availability in shipbuilding[J] .Journal of Jiangsu University of Science and Technology :Natural Science Edition, 2006, 20(6):5.

[8] Kim Y,Gotoh K,Toyosada M. Global cutting-path optimization considering the minimum heat effect with microgenetic algorithm s[J] .Journal of Marine Science and Technology,2004, 9(2):70.

[9] 高伟增, 张宝剑, 陈付贵, 等.基于遗传算法的切割路径优化[J] .西南交通大学学报, 2005, 40(4):457.GAO Weizeng,ZH ANG Baojian, CH EN Fugui,et al .Optimization of cutting path based on genetic algorithm[J] .Journal of Southw est Jiaotong University,2005, 40(4):457.

[10] 田剑.船用钢板切割车间生产调度优化研究[J] .成组技术与生产现代化, 2009, 26(1):15.TIAN Jian.Study on production scheduling optimization of ship steel plate cutting workshop[J] .G roup Technology &Production Modernization, 2009, 26(1):15.

[11] 谷峰.柔性作业车间调度中的优化算法研究[D] .合肥:中国科学技术大学, 2006.GU Feng .Optimization algorithm of flexible job shop scheduling[D] .Hefei:University of Science and Technology of China, 2006.

[12] 吴秀丽.多目标柔性作业车间调度技术研究[D] .西安:西北工业大学, 2006.WU Xiuli .Research on multi-objective flexible job shop scheduling problem [D] .Xi' an:Northw estern Poly technical University,2006.

[13] 刘宝碇, 赵瑞清, 王纲.不确定规划及应用[M] .北京:清华大学出版社, 2003.LI U Baoding,ZHAO Ruiqing,WANG Gang .Uncertain programming with application [M] .Beijing : Tsinghua University Press, 2003.

[14] Charnes A,C ooper W W .Chance-constrained prog ramming[J] .Management Science,1959, 6(1):73.

[15] LIU B D .Dependent-chance programming :a class of stochastic optimization [J] . Computers & Mathematics with Applications, 1997, 34(12):89.

[16] Rossi R, Tarim S A, Hnich B, et al.A note on Liu-Iw amura' s dependent-chance programming [J] .European Journal of Operational Research,2009, 198(3):983.