汽车后视镜气动噪声的影响参数

李启良 ,杨志刚 ,王毅刚

(1.同济大学航空航天与力学学院, 上海200092;2.同济大学汽车学院, 上海201804)

后视镜产生的气动噪声影响着车内外声场环境,成为近几年的研究热点.美国通用汽车公司[1]于2008 年在GMAL 风洞对GMT360 车型和GMX320车型的后视镜进行气动噪声试验测量, 并利用测量结果评估FLUENT 软件用于气动噪声预测的可行性.奥地利研究中心[2]于2005 年在BMW 风洞对BMW5 系列的后视镜进行试验测量,并利用试验结果评估其数值计算的合理性.过去的研究对量产车的后视镜所产生气动噪声做了少量的风洞试验, 并开始尝试评估数值计算的可行性.然而,这些研究缺乏通用性, 难以直接指导后视镜的设计和开发.

在后视镜设计开发中, 工程师与研究者注意到后视镜产生的气动噪声是后视镜与A柱之间相互作用的结果, 噪声大小和分布受后视镜的外形、安装角度等多种因素影响.为了更清楚辨别出这些因素的变化规律, 本文从真实后视镜的基本元素(前脸、后脸和支架)出发,抽象出普通后视镜.在普通后视镜基础上,依据已有气动优化经验, 选取表征后视镜形状的3 个参数和安装角度的2 个参数, 它们分别是前脸厚度L、后脸深度d、支架长度h、迎风角度θ以及旋转角度α.通过考察它们的差异, 评估它们的变化规律,旨在为后视镜优化设计提供参考.

1 数值计算方法

1 个直径D和高度H均为0 .2 m 的半圆柱以及直径D为0 .2 m 的1/4 球组成的普通后视镜首先被安装在长度为15 .00D、宽度为8 .00D以及高度为7 .20D的计算域中,且远离入口约为5 .25D,如图1所示.商业软件ICEM-CFD 用于在整个计算域内创建六面体网格.为了能更好求解壁面边界层, 在后视镜表面和地面创建边界层网格.考虑到大涡模拟对网格的特殊要求,设定第1 层网格到后视镜壁面量纲一化的距离y+≈5 .整个计算域初始网格总数约为270 万个.无粘壁面条件应用到计算域的2 个侧面和顶面;无滑移的壁面条件应用到地面和后视镜表面.在计算域的入口指定为速度入口, 设定其雷诺数Re=520 000(以后视镜直径为特征长度);出口指定为压力出口.

图1 数值模型示意Fig .1 Schematic of numerical model

直接方法与混合方法在气动噪声预测中均有应用.直接方法通过对整个计算域的流场和声场进行求解,从而实现气动噪声预测.该方法要求巨额计算资源, 仅适用于雷诺数较小的流动产生的气动噪声问题.本文使用的混合方法通过将流场和声场分开计算, 即首先通过大涡模拟获得后视镜表面以及支撑面的压力脉动, 然后利用FW-H 方程得到不同位置的噪声特征,它可以大幅度降低计算资源, 从而能够用于雷诺数较大的流动产生的气动噪声问题.计算时,首先使用可实现两方程k-ε(kinetic energy-dissipation rate)湍流模型[3]得到流场的准定常解,然后使用大涡模拟计算后视镜非定常流场, 其中亚格子模型选用Smagorinsky-Lilly 模型[4].在非定常流动计算中, 初始时间步长设定为5 ×10-4s ,单个时间步长内迭代25 次, 通过监控测点A与B确定单个时间步长计算收敛.计算3 000 个时间步长后,保持单个时间步长迭代步数不变,将时间步长调整为2 .5 ×10-4s ,继续计算1 000 个时间步长后,开始采集测点数据,接下去的2 000 个时间步长的计算结果用于数据分析.

以普通后视镜作为基础模型, 在此基础上分别对可能影响后视镜气动噪声的3 个外形参数和2 个角度参数进行气动噪声计算与分析,如图2 所示.变化后的后视镜同样安装在图1 所示的计算区域, 使用相同的网格处理技术,最终创建的网格总数与基础模型的网格总数有些差异.对于它们的气动噪声计算, 包括边界条件、湍流模型、时间步长以及数据采样等等均与基础模型相同.

图2 5 种后视镜参数Fig .2 Five parameters of rear view mirrors

2 结果分析与讨论

2 .1 数值与试验结果对比

为了验证本文后视镜气动噪声预测结果的准确性,选取了1999 年在德国FKFS 气动-声学风洞完成普通后视镜的气动噪声试验结果[5-6].图3 给出该试验示意图以及测点布置.多达11 个传声器测点按照图3b 和图3c 的位置进行先后布置.限于篇幅,图4 仅给出测点4 的频谱特性.从图中可以看出,随着频率增加, 测点声压级不断减少.当测点超过1 000 Hz后,测点声压级已经处于40 dB .可见, 后视镜产生气动噪声主要能量集中在中低频区域, 其频率段为20～500 Hz .对比数值与试验结果可以发现,数值计算得到测点频谱与试验较为相似.特别是在频率较低处,如频率为20～100 Hz ,数值与试验不仅趋势一致, 而且数值相差很小.当频率较大时, 如频率200～1 000 Hz,且数值得到测点声压级变化趋势虽然一致, 但普遍比试验大.这可能是由于数值计算本身原因导致,如亚格子模型、网格等因素.从计算数值与试验在频率从20 Hz 到2 000 Hz 得到测点4的总声压级可以看出,它们总声压级在80 dB 附近变化,两者相差约0 .3 dB .

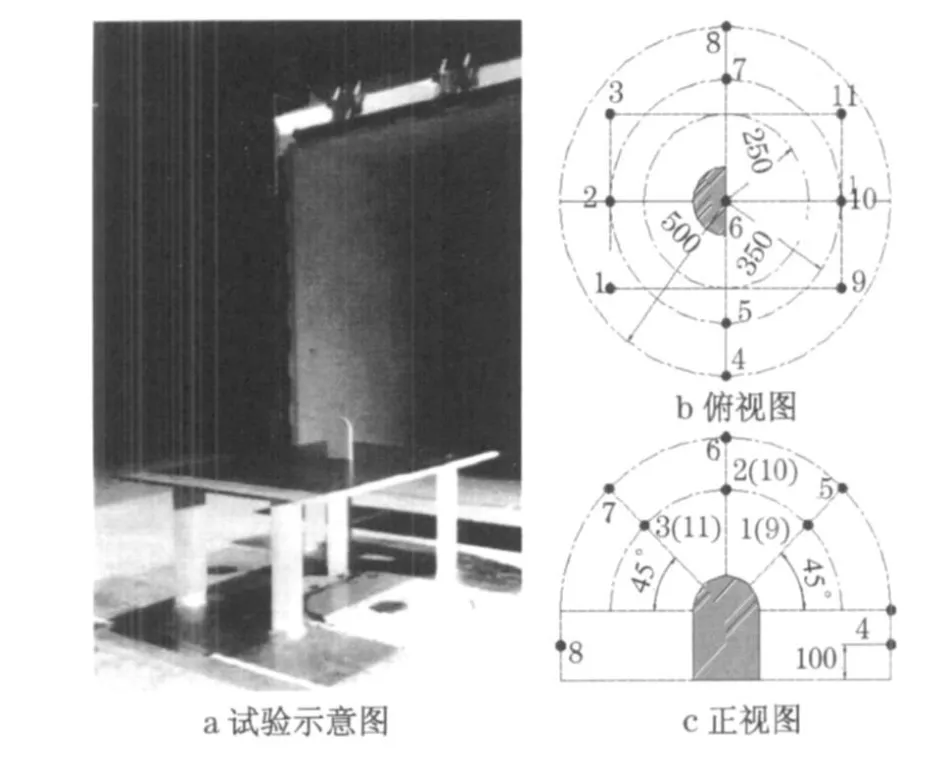
图3 风洞试验与测点布置(单位:mm)Fig.3 Wind tunnel test and test point positions(unit:mm)

图4 测点频谱Fig .4 Frequency spectrum of test points

2.2 不同形状参数的影响

图5 显示了不同形状参数下后视镜表面和支撑面的声压级.对于普通后视镜表面正对来流部位, 特别是驻点附近, 由于该处压力脉动非常小,其声压级很小.处于分离点附近的流动很不稳定,导致后视镜表面较大的压力脉动是当地声压级较大的主要原因.尾涡的持续不断拍打使后视镜后脸声压级可达105 dB .后视镜尾部流场十分复杂, 非定常流动计算表明该处存在各种尺度的涡结构,各种涡之间的相互作用导致支撑面上强烈的非定常压力脉动,脉动振幅超过后视镜本身.正因如此,在支撑面处声压级分布呈现梯形形状,其他的声压级远大于后视镜本身,最大声压级可达128 dB ,绝大多数地方的声压级在110 dB 以上.其中,梯形上底可取后视镜后脸与支撑面交界线,高约3 .5D,斜边与上底夹角约为105°.

当前脸厚度增加后, 由于流动分离点后移, 后视镜表面压力脉动和尾部速度脉动振幅降低,声压级有所降低.支撑面上最大声压级从基础模型的128 dB减少到123 dB .梯形的分布形状仍然存在,但是梯形所围面积有所减少.可见增加后视镜前脸厚度可降低声源的强度.后视镜后脸深度的增加,减少了后脸的压力脉动, 使它的声压级有轻微减少.支架的存在从根本上改变了后视镜尾部流场.从支撑面声压级云图可以看出,梯形分布形状转变成矩形,其中矩形的宽约为1 .50D,长约为2 .00D.在矩形内,大部分位置的声压级均大于110 dB ,最大声压级可达127 dB .与基础模型相比可以发现,支架的存在有利于降低声源的强度.

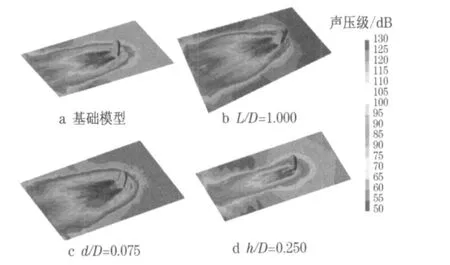
图5 声源表面声压级(f =125 Hz)Fig.5 Sound pressure level of source surfaces(f =125 Hz)

位于后视镜尾部的测点A用于感受声源的声传递.不同形状参数下测点的频谱图如图6 .从图中可以看出,随着频率增加,各种形状参数的后视镜均有相同的变化趋势,即均随着频率增加,声压级不断下降,在频率为50 Hz 附近有一个不太明显的峰值.与基础模型相比, 除高频外,在相同频率下形状参数变化后的后视镜声传递到测点的声压级均有不同程度降低, 其中在频率位于200～700 Hz 处降幅较为明显.在基础模型的基础上, 后视镜前脸厚度增加后,相同测点感受到的总声压级有所减少, 如基础模型测点A的总声压级为115 .6 dB,但前脸厚度增加后,该测点的总声压级为112 .3 dB ,降低了3 .3 dB .后脸深度的改变,仅稍微降低其总声压级.支架的存在对降低声源声传递也有贡献.与无支架的后视镜相比, 在有支架情况下,测点A感受到的总声压级降低了3 .6 dB .

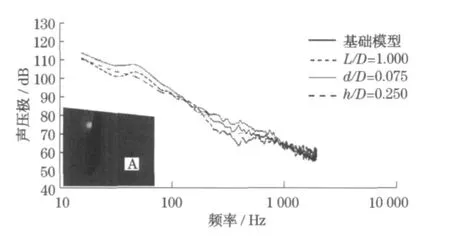
图6 测点频谱Fig .6 Frequency spectrum of test points

2 .3 不同角度参数的影响

迎风角度和旋转角度的变化并没有带来声源表面声压级分布的本质变化,如图7 所示.支撑面仍比后视镜表面声压级大,最大声压级同样为130 dB .对于迎风角度为15°时, 由于后视镜表面压力脉动变小而使其声压级有一定的降低.支撑面上梯形面积变小,这与当地流场变化密切相关.旋转角度为15°时,尽管梯形分布仍然存在, 但是其位置发生改变.梯形上底边不再是后视镜后脸与支撑面的交界线,而是与该交界线有一定的角度.声压级最大的地方仍是剪切层影响的区域, 其大小达130 dB .

图7 声源表面声压级(f =125 Hz)Fig.7 Sound pressure level of source surfaces(f =125 Hz)

仍取测点A来分析角度参数变化后后视镜的声传递,它们频谱如图8 所示.从图中可以看出, 尽管角度发生变化, 但并没有改变测点声压级随频率的变化趋势.与基础模型相比, 迎风角度增加后, 在频率小于700 Hz 的中低频段,测点A的声压级均有不同程度的减少.旋转角度增加后, 尽管在200～700 Hz的频率段有所降低,但在更低频段却增加.迎风角度增加的确能降低声源的声辐射强度,如迎风角度为15°,测点A的总声压级降低了1 .4 dB .但是旋转角度为15°, 测点A的总声压级反而增加了0 .6 dB .可见, 迎风角度对降低后视镜气动噪声有利,而旋转角度则是不利的.

图8 测点频谱Fig .8 Frequency spectrum of test point

3 结论

整车风洞普通后视镜气动噪声试验结果与数值计算结果的吻合证明了本文采用混合方法预测后视镜气动噪声的合理性.

尽管后视镜表面辐射出噪声, 但是后视镜支撑面辐射的噪声比后视镜本身大.在后视镜的支撑面声压级分布呈现梯形形状, 不随后视镜前后脸的变化而变化, 但支架的存在却改变了该区域的分布,使之成为矩形分布形状.

通过增加后视镜前脸厚度、后脸深度、支架长度与迎风角度能降低后视镜产生的气动噪声,但增加旋转角度却不能.

[1] Chen K H,Johnson J, Dietschi U,et al.Automotive mirror wind noise simulations and wind tunnel measurements[C] ∥Proceeding s of the 14th AIAA/ CEAS Aeroacoustics Conference.Vancouver :American Institute of Aeronautics and Astronautic, Inc, 2008:1-13.

[2] Reichl C,Krenn C,Mann M, et al.Application of numerical and experimental techniques for the Aero-acoustic characterisation of a car rear-view mirror [J] .International Journal of Aeroacoustics, 2005, 4(1):185.

[3] Shih T H,Liou W W,Shabbir A,et al.A newk-εeddy viscosity model for high Reynolds num ber turbulent flow s :model development and validation[J] .Computers and Fluids ,1995, 24(3):227.

[4] Lesieur M, Metais O,Comte P .Large-eddy simulations of Turbulence[M] .London:Cambridge University Press, 2005.

[5] Hö ld R, Brenneis A,Eberle A .Numerical simulation of aerodynamic noise sound generated by generic bodies placed on a plate :part Ⅰ-prediction of aerodynamic noise sources[C] ∥Proceeding s of the 5th AIAA/ CEAS Aeroacoustics Conference .Washington: American Institute of Aeronautics and Astronautic, Inc, 1999:1-14.

[6] Siegert R,Schw arz V,Reichenberger J.Numerical simulation of aerodynamic noise sound generated by generic bodies placed on a plate :Part Ⅱ-Prediction of Radiated Sound Pressure[C] ∥Proceeding s of the 5th AIAA/ CEAS Aeroacoustics Conference .Washington: American Institute of Aeronautics and Astronautic, Inc, 1999:1-10.