铰接式岔枕道岔结构落轴冲击数值分析

朱剑月

(同济大学 铁道与城市轨道交通研究院, 上海200092)

跨区间无缝线路的大量运用使得作为轨道结构薄弱环节的道岔成为限制行车速度的最主要部位[1].目前,各国新型设计的高速与提速道岔逐步采用混凝土岔枕,较木枕其具有整体性强、稳定性好及使用寿命长等优点.但根据多年运营发现,混凝土岔枕的采用使得岔区轨道结构刚度过大及不等长岔枕形成沿线路纵向的刚度不平顺,造成列车高速过岔时对轨道结构产生附加冲击动力,导致岔枕产生裂纹、掉块等损伤以及未行车股道岔枕末端翘起并拍打道床,加速道砟粉化,致使道床断面形状难以保持,不利于维持线路的良好状态.为解决此类问题和简化预组装道岔的储运与装卸、避免整组道岔运输超限,德国铁路提出了采用铰接式岔枕的新理念[2-3],即两岔枕通过弹性铰联结组成长岔枕.

近年来,多数道岔动力学模型集中在轮轨相互作用的研究[4-5],文献[6] 考虑联结铰的作用,假定在承受相同轮载下,初步分析了铰接式与普通岔枕轨道结构的受力与动态响应.

由于轮轨间的相互耦合作用, 铰接式与普通岔枕的道岔结构承受的轮载会有所不同.本文拟采用有限元方法,建立整组道岔模型, 比较分析落轴冲击下铰接式与普通岔枕轨道结构的动力特性,为铰接式岔枕(含铰接件)的设计与高速道岔结构的进一步优化提供理论基础.

1 分析模型

1 .1 道岔结构有限元模型

根据12 号可动心轨辙叉单开提速道岔布置图,建立道岔结构落轴冲击有限元模型.忽略不等长铁垫板、滑床台及间隔铁等部件的影响,道岔轨下弹性胶垫的刚度(或阻尼)相同,以弹簧阻尼单元模拟;钢轨(或岔枕)与心轨(或翼轨)采用等截面和变截面Timoshenko 梁单元模拟;岔枕底部在道砟颗粒间作浮沉运动时, 往下运动形成的刚度与阻尼较往上时大,另未行车股道岔枕末端上翘后, 除受到翘起端自重弯矩外,道床将不对其提供支承力,故采用非线性弹簧阻尼单元进行枕下基础模拟.

1.2 落轴冲击有限元模型

车轮采用实体单元离散, 按照总质量不变将其处理为等厚度, 由一定高度作自由落体运动撞击钢轨.根据接触面间动力学和运动学条件,两接触面间法向接触力为压力以及两接触体位形在运动过程中不可相互贯穿, 与落轴冲击轮轨接触相联系的力平衡条件与位移连续性条件为

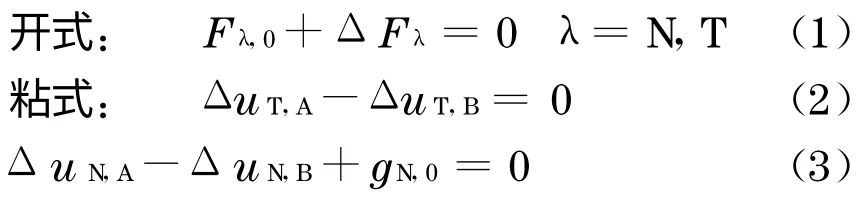
式中:FN和FT为钢轨作用于车轮踏面的法向接触力和切向摩擦力;uN与uT分别为车轮(或钢轨)的法向与切向位移;下标A 代表车轮;下标B 代表钢轨;gN,0为轮轨间初始间隙.

式(1)～(3)用于判断轮轨接触状态的变化:开式状态下,车轮踏面离开轨面, 接触约束释放, 轮轨间法向接触力和切向摩擦力及其增量为零;粘式状态下,车轮接触轨面, 轮轨间无相对滑动, 轮轨间切向位移增量为零,同时,轮轨接触对之间的法向位移增量等于其初始间隙.落轴冲击采用点线接触单元模拟, 通过在线跟踪接触点与目标线的相对位置,确定两者之间的接触协调关系, 以模拟轮轨间存在着瞬时接触、分开的交错运动.

根据有限元法, 将轮轨接触边界条件(1)～(3)采用罚函数法释放, 得到轮轨接触有限元控制方程

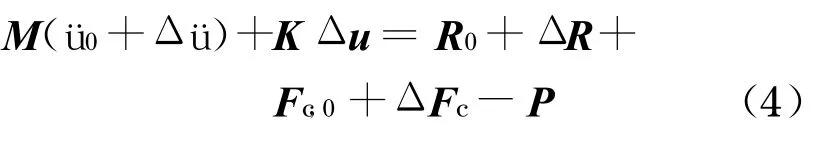
式中:M, K 为质量和刚度矩阵;u 为位移;R 为节点载荷向量;Fc 为接触力引起的节点载荷向量;P 为等效于单元应力的节点力向量;u0,R0,c与Fc,0分别为u,R 与Fc的初始值.

由式(4)求得位移后,按照式(1)～(3)判断轮轨接触状态, 再根据Newmark 法计算出速度和加速度.

该落轴冲击数值分析方法已由现场实测进行了验证, 请见文献[7-8] .

1 .3 联结铰计算模型

考虑轨道结构的整体稳定性及便于施工维护,铰接式岔枕的联结铰设置于道岔侧股股道中部、两连接轨枕顶部(如图1 所示),采用柔性铰形式,提供一定的平移、竖向、弯曲及转动弹性与阻尼,以缓和高速列车的振动冲击.联结铰采用三维弹性铰链单元模拟,每单元有2 个节点, 每节点含3 个平动(u,v,w)和3 个转动(θx,θy,θz)自由度,其单元刚度、质量与阻尼矩阵均为12 行12 列,各自由度次序为(u1,v1,w1,θx1,θy1,θz1,u2,v2,w2,θx2,θy2,θz2),其中:x和u沿线路纵向,y和v为横向,z和w为垂向.

图1 铰接式岔枕联结铰布置Fig.1 The arrangement chart of the joint in the articulated switch sleeper

三维弹性铰链单元质量矩阵Me为

式中:M为单元总质量;Im为单元总转动惯量, 为简化计算,三方向相同.

单元刚度矩阵Ke为

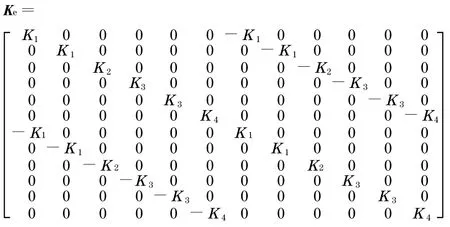
式中:K1,K2,K3,K4分别为单元平移、竖向、弯曲(关于x与y向)及转动刚度(沿垂向z).假定x与y向的平移与弯曲刚度均相同.

除了沿垂向转动外, 其余自由度方向的阻尼均被忽略,单元阻尼矩阵Ce为

式中:Ct为单元绕垂向的转动阻尼系数.

1.4 计算参数

道岔基本轨与翼轨为60 kg · m-1钢轨,弹性模量2 .1 ×1011N ·m-2,泊松比0 .3,沿水平轴的截面惯性矩为3 .217 ×10-5m4;岔枕采用60 号混凝土,弹性模量3 .65 ×1010N · m-2,泊松比0 .15 ,沿水平轴的截面惯性矩为2 .66 ×10-4m4;轨下胶垫厚5 mm,扣件刚度为180 kN · mm-1,阻尼为1 .6 ×105N · s · m-1,高弹性扣件刚度则为30 kN ·mm-1,阻尼为1 .2 ×105N ·s ·m-1;道床竖向向下刚度60 kN ·mm-1,阻尼4 .5 ×105N ·s ·m-1,竖向向上刚度12 kN · mm-1,阻尼1 .5 ×105N · s ·m-1,当岔枕离开道床面,枕下支承刚度消失;考虑重点研究道岔结构的垂向动力性能,铰接式岔枕的联结铰平移及转动刚度保持不变,分别为106N ·m-1与5 ×104N · m ·rad-1,其竖向及弯曲刚度的变化范围104～109N · m-1,阻尼均取8 ×104N ·s ·m-1.

落轴车轮质量为0 .6 t ,轮轨冲击发生在辙叉区心轨尖端相邻两岔枕轨枕间距跨中截面处的钢轨顶部,落高为10 ,25 与40 mm ,计算心轨尖端岔枕处轨道结构的动力响应.除岔枕端部的动力响应外,其余钢轨与轨枕的动力响应均位于心轨下轨枕座位置.

2 动力响应分析

2 .1 时域内动力响应分析

直股落轴冲击下辙叉区心轨下铰接式岔枕及其未行车股道端部(联结铰竖向及弯曲刚度为104N ·m-1,落高40 mm ,扣件刚度180 kN ·mm-1的振动响应曲线如图2 所示, 可以发现:落轴冲击时,轨道结构在极短时间内产生了多次瞬态振动,第1 次响应最为剧烈, 然后迅速衰减, 与实测波形[9]取得很好一致;铰接式岔枕心轨下轨枕座与末端位置的加速度响应曲线相位相反, 即行车股道轨下岔枕下沉(或反弹), 未行车股道一端将反翘(或拍击道床).另外, 数值模拟表明,落轴冲击作用下的道岔结构动态响应均随落高的增加而显著增大.根据道岔结构落轴冲击的计算结果(表1),铰接式岔枕轨道结构的动力性能分析如下.

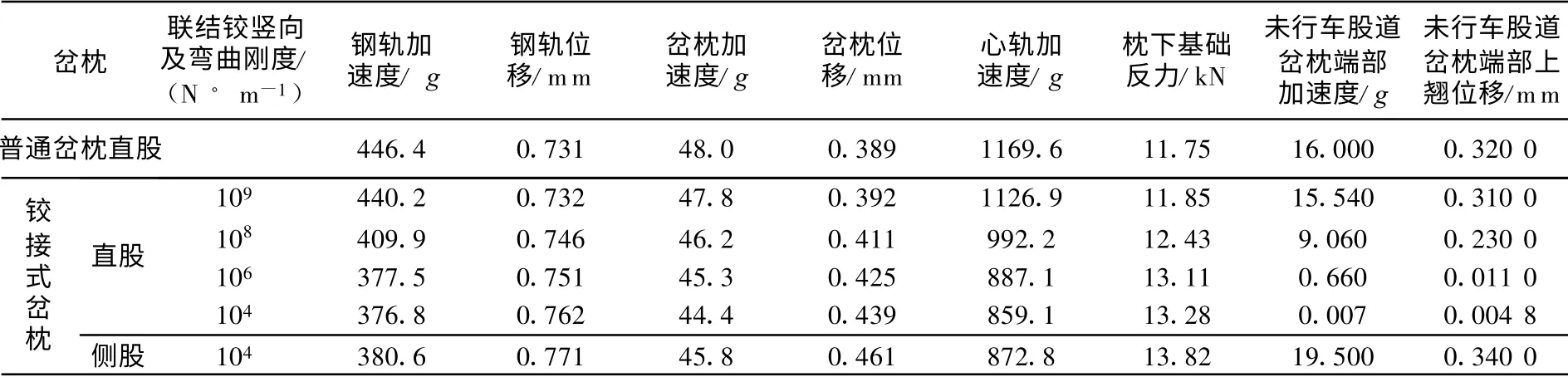
表1 铰接式和普通岔枕轨道结构落轴冲击响应的变化趋势(扣件刚度180 kN· mm-1)Tab.1 Comparison of the dynamic response between the articulated and integral switch sleeper under wheel load drop(fastener stiffness 180 kN · mm-1)

(1)与普通岔枕的道岔结构相比, 铰接式岔枕轨道结构的钢轨与岔枕位移、枕下基础反力较大,而钢轨、心轨与岔枕加速度则较小.如联结铰竖向及弯曲刚度为104N · m-1时,铰接式岔枕的钢轨与岔枕位移、枕下基础反力较普通轨枕增加约4 .2 %,12 .9 %与13 .0 %,而钢轨、心轨与岔枕加速度降低了15 .6 %,26 .5 %与7 .5 %.显然,由于铰接式岔枕联结铰的作用,使得道岔结构整体刚度较低,一定程度上缓和了车轮对轨道结构的动力冲击.

(2)随着联结铰竖向及弯曲刚度的增大, 铰接式岔枕轨道结构的钢轨、心轨与岔枕加速度响应逐渐减增小加;当,钢联轨结与铰岔竖枕向位及移弯、枕曲下刚基度础大反于力1等09响N应·逐m渐-1时,铰接式岔枕的动态特性基本等同于普通岔枕.因此,铰接式岔枕的联结铰需合理设置,其相应的各向刚度值应进行参数优化, 以有效改善列车过岔时轨道结构的动力性能.

(3)道岔某一股道的线路上行车时, 另一未行车股道的岔枕末端产生了一定的上翘位移量,如普通长岔枕心轨下轨枕向下位移为0 .389 0 mm, 其未行车股道岔枕端部向上位移也达到了0 .320 0 mm .长岔枕端部翘起位移量增加, 将不利于保持一股轨道动两.联侧结钢铰轨竖的向水及平弯,曲同刚时度会为拍1击04道N床·,m致-使1时道,床 铰松接式岔枕轨枕端部上翘量(0 .004 8 mm)仅为普通岔枕(0 .320 0 mm)的1/67 ,这极大地削弱了高速列车过岔时未行车股道长岔枕末端翘起和对道床的拍打,减少了道砟颗粒的破损与粉化.

(4)对于普通岔枕, 未行车股道岔枕端部加速(度加联达速结度1铰60.刚 0.00度00 7 g 1g,0 (远6联 N大结·于 铰m铰刚-1接度)式.1同0岔4样 N枕 可·未 见m行-:列

1车)车或股 过0道.岔6一6时0端g,普通长岔枕未行车股道末端振动加速度越大对道床的夯拍作用就越强, 易造成岔枕开裂、道砟石料破碎及道床断面形状难以保持, 不利于维持线路的良好状态;而铰接式岔枕的采用,则很大程度上避免了类似轨道结构伤损.

(5)铰接式岔枕未行车股道岔枕端部加速度和位移随联结铰竖向及弯曲刚度的增大逐渐增加;联结铰竖向及弯曲刚度小于106N·m-1时, 铰接式岔枕端部的加速度和位移响应较普通轨枕显著减少.

(6)铰接式岔枕侧股落轴下未行车股道岔枕端部(位于长工作边)的加速度与上翘位移显著增加,远大于直股落轴下未行车股道岔枕端部(位于短工作边)的响应,也较普通岔枕直股落轴下未行车股道岔枕端部的响应大(端部加速度与上翘位移分别增加约21.9 %与6 .3%),其余钢轨、心轨与轨枕等动力响应均有所增加,但增幅不大(小于5 %).为便于比较,直股与侧股落轴冲击均采用了40 mm的落高,实际上,车辆侧向过岔速度较低,相应的轮轨动态相互作用也较小.

2 .2 频域内动力响应分析

铰接式(联结铰刚度104N · m-1)与普通岔枕心轨下轨枕座位置的钢轨与轨枕振动加速度级的1/3倍频程如图3 所示,可以发现:多数频域范围内,普通岔枕的钢轨与轨枕的加速度级高于铰接式岔枕;在125 Hz 左右出现一峰值,对应于车轮质量在轮轨接触弹簧与道岔结构刚度上的共振频率;同时,落轴冲击下,钢轨加速度振级的幅值明显高于轨枕.

3 刚度与联结铰参数优化

3 .1 轨下刚度参数优化

德国铁路道岔区采用高弹性扣件, 速度为220 km · h-1及以上的线路采用轨道整体刚度为17 .5 kN ·mm-1[3,10],岔区动静刚度比为1 .2～1 .3 ,有必要进一步分析扣件动刚度较低时铰接式岔枕道岔结构的振动特性.扣件刚度为30 kN · mm-1时, 道岔结构直股承受落轴冲击下的计算结果如表2 所示.

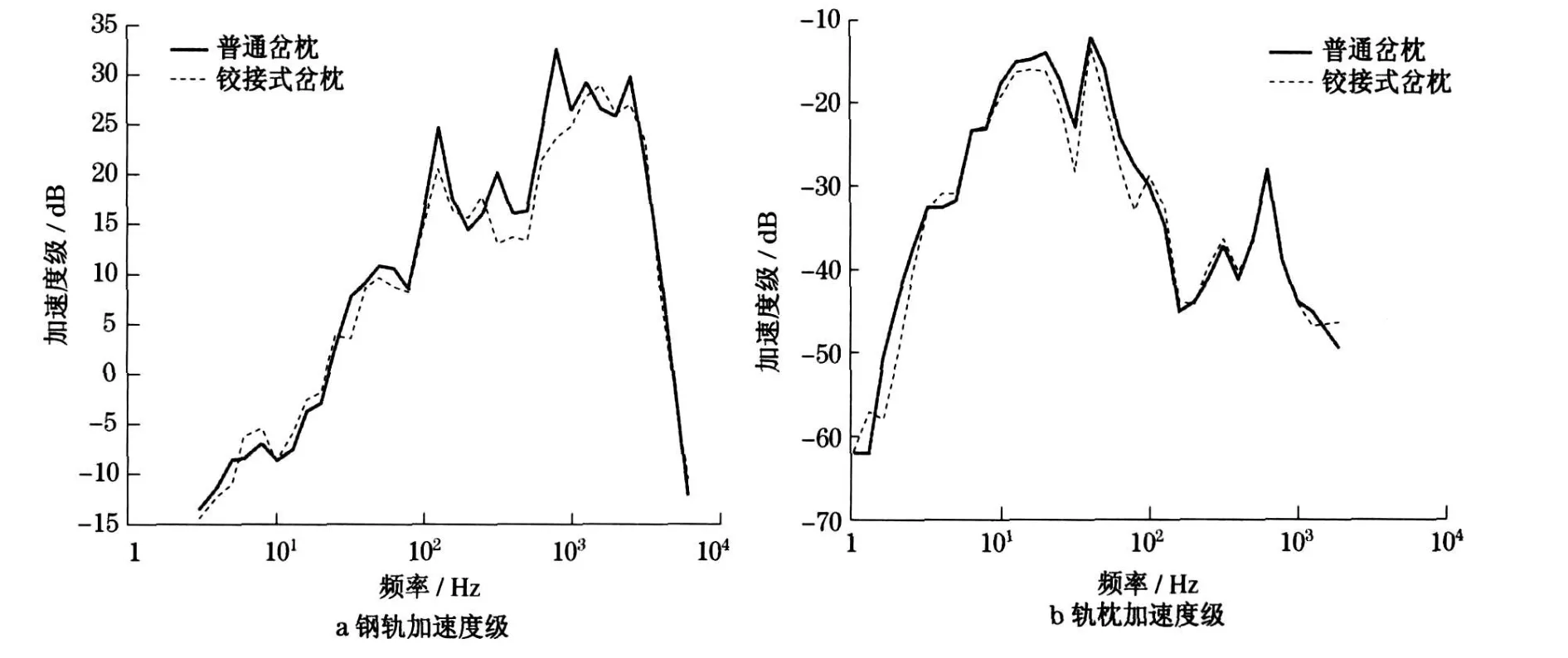
图3 1/ 3倍频程中心频率处钢轨与轨枕的振动加速度级(参考值为1g)Fig .3 1/ 3 octave spectra of rail and sleeper acceleration(reference value 1g)

比较表1 与表2 可知:扣件刚度为30 kN ·mm-1时,随着联结铰竖向及弯曲刚度的增大,铰接式岔枕轨道结构落轴冲击响应的变化趋势与扣件刚度为180 kN ·mm-1时的基本一致;扣件刚度降低后,轨道结构产生的动力响应中除了钢轨位移与加速度以及心轨加速度有所增加外, 枕下基础反力、岔枕及其未行车股道端部位移与加速度均明显降低.如扣件刚度为30 kN · mm-1较扣件刚度为180 kN ·mm-1(联结铰竖向及弯曲刚度为106N ·m-1)时的铰接式岔枕轨道结构的钢轨位移、加速度与心轨加速度增加了21 .4 %, 27 .0 %与24 .8 %, 枕下基础反力、岔枕位移与加速度则降低了15 .8 %,16 .2 %与33 .1 %,未行车股道岔枕端部位移与加速度也均减小了27 .3 %.因此,道岔区高弹性扣件的采用将与铰接岔枕组合成优良的弹性基础,使得较多岔枕共同承受车轮荷载, 降低了岔枕的动态位移量,并进一步减缓岔枕末端的反弹和拍击道床,从而减少道砟颗粒的破碎和粉化,延长道床养修周期.

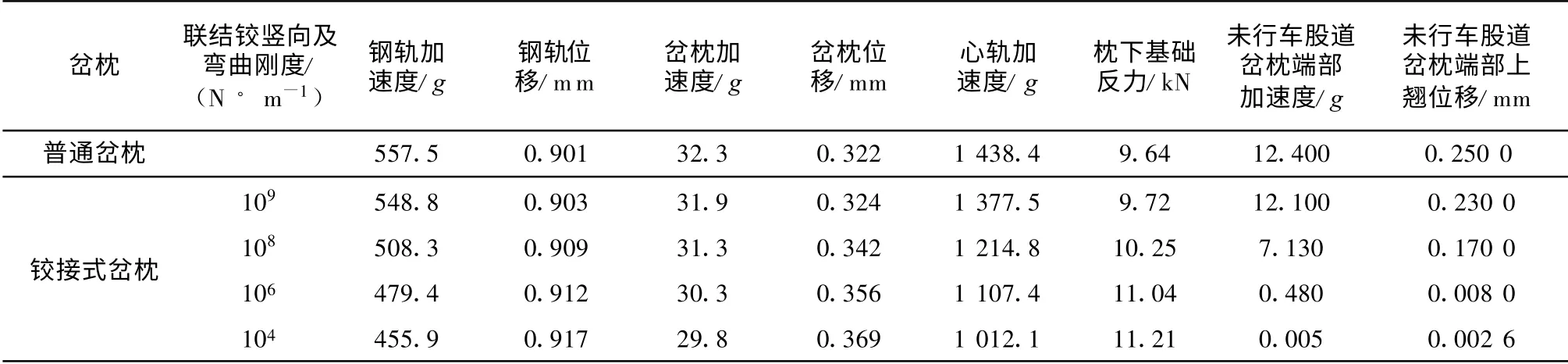
表2 铰接式和普通岔枕轨道结构落轴冲击响应的变化趋势(扣件刚度30 kN· mm-1)Tab.2 Comparison of the dynamic response between the articulated and integral switch sleeper under wheel load drop(fastener stiffness 30 kN · mm-1)

3.2 联结铰参数优化

分析铰接式岔枕联结铰直股落轴下的冲击响应(表3)可得:道岔区钢轨下采用高弹性扣件, 铰接式岔枕联结铰的加速度与位移等响应有所下降,有利于减缓联结铰受到的振动冲击;由于联结铰设置于道岔侧股股道中部(图1),当列车在道岔直股上运行时,联结铰位于长枕端(靠近直股一侧)的加速度与位移响应均远大于短枕端(联结铰竖向及弯曲刚度小于106N ·m-1).因此, 铰接式岔枕的联结铰设计时, 可采用短枕端的铰接件较长枕端适量加宽的变截面方式, 使位于长枕端的铰接件弯曲刚度低于短枕端,以配合与协调现场列车运行时联结铰的实际变形.

考虑未行车股道岔枕端部加速度及其上翘位移量不宜过大以防止其拍打道床和尽量减小联结铰两端的动力响应差异, 建议铰接式岔枕联结铰的竖向及弯曲刚度值位于104～106N ·m-1之间,相应的道岔区轨下弹性扣件动刚度的取值范围则为25～35 kN ·mm-1.

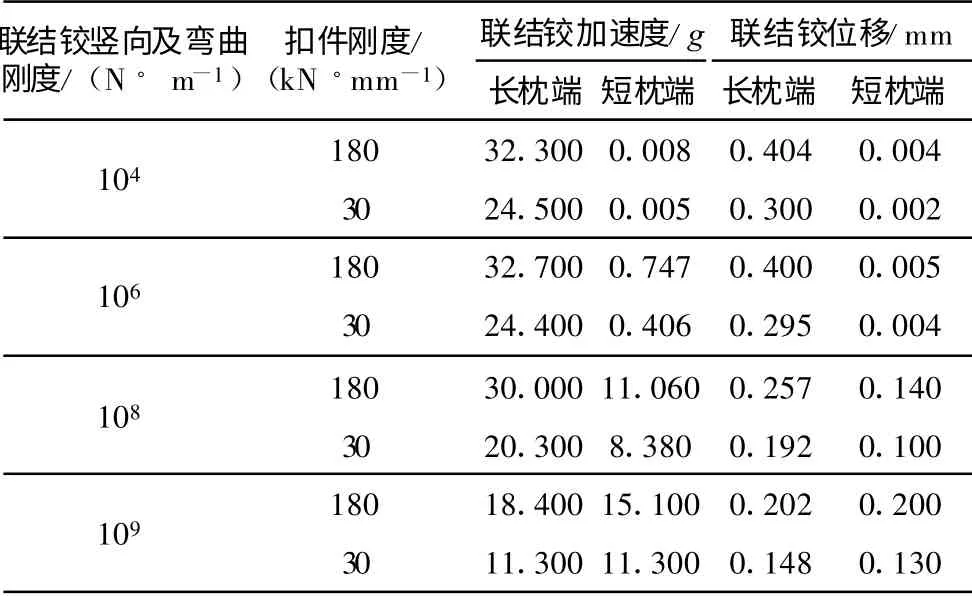
表3 铰接式岔枕联结铰落轴冲击响应的变化趋势Tab.3 Variation of dynamic response of joints in the articulated switch sleepers under wheel load drop

4 结论

通常,落轴作为一种试验方法, 被广泛应用于轨道结构的振动参数测定及其动力性能的评价,本文则运用有限元法进行落轴冲击的数值模拟,计算分析了铰接式和普通长岔枕道岔结构的振动响应.与普通结构相比, 铰接式岔枕道岔结构的优点在于:轨道结构整体刚度较低, 与道岔区高弹性扣件组合成优良的弹性基础,优化了高速道岔的动态特性;改变了普通岔枕的变形曲线, 使得较多岔枕共同承受车轮荷载,减少了岔枕动态位移量, 较大程度上降低了未行车股道岔枕末端对道床的拍击, 减少了道砟粉化,延长了道床养修周期.

近年来,通过引进消化吸收与再创新, 我国高速道岔技术取得了长足进步, 研制成功了时速250 km ·h-1与300 km ·h-1及以上速度的道岔,铰接式岔枕也已初步开发成功并进行了线路试验, 本文通过落轴冲击有限元分析所得铰接式岔枕道岔结构的动态特性规律有待于现场运行线路的实测验证.

[1] 何华武.时速250km 级18 号道岔设计理论与试验研究[J] .铁道学报, 2007, 29(1):66.H E Huaw u.Research on the design theories and experiments of the 18 #turnout under 250 km · h-1[J] .Journal of the China Railway Society,2007, 29(1):66.

[2] Schultz P,van Dranen C . Pre-assem bled turnouts cut installation times[J] .Railway Gazette International, 2004, 160(1):30.

[3] 郭福安.国外高速铁路的道岔设计[J] .中国铁路, 2006(2):48.GUO Fuan.T he design of turnout in foreign high-speed railway s[J] .Chinese Railways, 2006 (2):48.

[4] Kassa E,Andersson C,Nielsen J C O .Simulation of dynamic interaction between train and railway turnout [J] .Vehicle Sy stem Dynamics, 2006, 44(3):247.

[5] Alfi S, Bruni S.Mathematical modelling of train — turnout interaction[J] .Vehicle Sy stem Dynamics, 2009, 47(5):551.

[6] 朱剑月.铰接式岔枕受力与振动响应分析[J] .同济大学学报:自然科学版, 2009, 37(1):73.ZH U Jiany ue.Comparison investigation on acting force and dynamic behavio r of articulated sw itch sleeper in turnout sy stem[J] .Journal of Tongji University :Natural Science ,2009, 37(1):73.

[7] 朱剑月, 练松良.轨道结构落轴冲击动态响应有限元分析[J] .铁道学报, 2005, 27(3):76.ZH U Jiany ue, LIAN Songliang .Railway track structure dynamic response under w heel load drop by use of FEM[J] .Journal of the China railway society,2005, 27(3):76.

[8] ZH U J Y .Analysis of dynamic behavior of low vibration track under w heel load drop by a finite element method algorithm[J] .Proceeding s of the Institution of Mechanical Engineers ,Part F :Journal of Rail and Rapid Transit, 2008, 222:217.

[9] 练松良.轨道动力学[M] .上海:同济大学出版社,2003.LIAN Songliang .Railway track dynamics [M] .Shanghai :T ongji University Press, 2003

[10] 卢祖文.客运专线铁路轨道[M] .北京:中国铁道出版社, 2005.LU Zuw en.Passenger traffic railway track[M] .Beijing :China Railway Publishing H ouse,2005.