高速公路追尾机理概率分析及风险评价

陆斯文, 张兰芳, 方守恩

(同济大学 道路与交通工程教育部重点实验室, 上海201804)

目前, 研究学者主要采用基于历史事故数据的多元回归统计法和非事故数据的理论推导法来对追尾事故成因及风险进行分析[1-2].由于基于历史事故数据的统计分析方法需要收集大量长期事故数据及天气、交通等关联数据,因此, 相对而言, 基于非事故数据的理论推导法更适合我国高速公路追尾事故特征的研究现状.而已有相关指标主要包含了临界减速度、临界制动距离、冲突碰撞时间以及以纵向跟驰安全间距为基础的追尾碰撞风险指标等[2].但上述追尾风险指标虽然能反映跟驰车辆在某一时刻固定不变的追尾风险度量,却不能在物理意义上体现出追尾事故潜在风险随机性和追尾事故发生的偶然性.因此,应采用概率统计的方法来研究分析高速公路追尾事故的发生机理及评估相应的追尾潜在风险性.在上述方法论的指导下,根据人-车碰撞风险计算方法[3],结合跟驰安全间距临界条件,考虑紧急情况下前后车紧急制动减速度、驾驶员反应时间的随机性及车辆制动协调时间, 建立高速公路追尾事故潜在风险指标.同时,也考虑到追尾碰撞过程中的能量损失,建立追尾事故严重程度风险评价指标.与文献[2] 相比,本文对导致追尾事故发生的随机性影响因素考虑更全, 而且综合考虑潜在追尾事故碰撞后的严重程度.

1 追尾事故机理

1 .1 追尾致因分析

高速公路行车过程中, 正常理性的驾驶人会根据引导车和自身车辆的物理运动状态保持与引导车合适的安全间距.而其安全间距的计算考虑了整个全制动过程[4],分为驾驶员反应阶段t1、制动器协调阶段t2、制动减速度增长阶段t3,具体以如下公式所示:

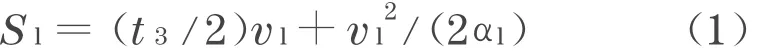
式中:S为制动距离;v为速度;α为加速度;下标l表示引导车。

后随车的制动距离

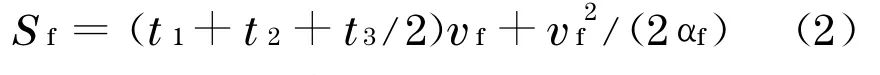
式中,下标f 表示跟随车.

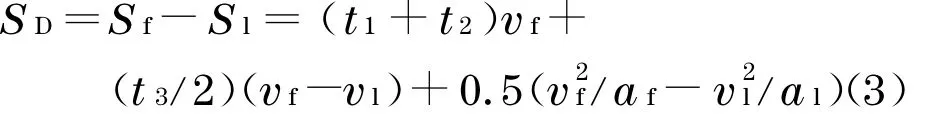
式中,SD为两车保持的安全间距.

因此,可以根据上述跟驰安全临界条件, 判断实际上后随车的车辆是否处于潜在的碰撞危险状态.当前车k和后车k+1 实际间距小于安全间距时,就有发生碰撞的可能性,具体公式如下:

式中:th,k+1是后随车k+1 到达前车k所在位置处的车头时距;SR是前后两车保持的实际净间距;Lk为前引导车k的车长.

通过上述公式转化后,可得到与文献[5] 类似的避免碰撞的最小临界加速度不等式,具体如下:

而车辆k+1 后面尾随车辆k+2 的最小临界加速度也可通过迭代式(5)得到

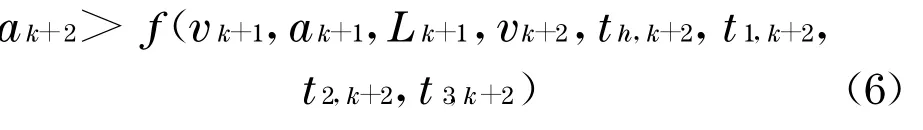
从式(5)和式(6)中可以发现一个有趣的现象.当前车k减速度增加而其他条件不变时, 后面车辆k+1 ,k+2 所需要的最小临界加速度也随之增加,说明车群中某辆车的减速度增加产生的影响会传递,导致后面所有的车辆减速度在原有基础上也相应增加,从而增大了后续车辆所需要的制动安全距离;同时当跟随车车头时距t′h,k+1与后随车反应时间t1,k+1、制动协调增长时间t2,k+1+t3/2 之差减小而其他条件不变时,后车所需要的最小临界加速度也随之增加.这意味,如果在车群中某辆车遇到障碍物突然紧急制动,而后随车的反应时间比较大,则其所需要的临界减速度将会增加.这导致其后续的车辆所需要的临界减速度也会增加,并使驾驶人在这种情况下产生的反应时间也通常会延长.如其他条件保持不变,一直传递下去, 往往有一辆车所需要的临界减速度超过其车辆所能获得的最大减速度,则两车追尾碰撞不可避免.因此, 追尾事故的发生主要有2 个因素:由于车群中某车紧急制动,追尾车辆未保持安全间距;车群中某些车辆反应时间过长, 导致后面的某一车辆采取制动也无效.但归根结底,内在原因就是前车因某种情况突然采取紧急制动,导致后随车反应不及时或即使采取紧急制动也发生了追尾碰撞事故.因此, 在车群行驶过程中,前车应尽量避免突然较大幅度的减速.

同时,根据文献[6] 的思想,追尾事故的发生可分为2 个阶段:第1 阶段前车减速, 对后车造成影响,形成一个干扰物;第2 阶段在前车减速情况下, 仍与后随车发生追尾碰撞事故.运用全概率公式的原理,假设E表示前车紧急制动减速事件,A表示追尾事故的发生.则追尾事故的发生可以表示成如下公式:

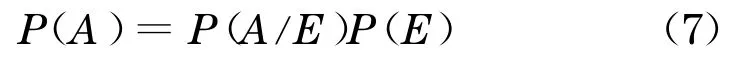
式中:P(A)为追尾事故事件A发生的概率;P(A/E)为在紧急制动条件下发生追尾事故的概率;P(E)为前车紧急制动减速发生的概率.

由于前车紧急制动发生的可能性与当时所处的跟驰环境相关, 如车流密度、平均车速、道路几何线形、天气状况等, 很难标定得出前车发生紧急制动的概率值.据此, 本文重点分析假设在前车紧急制动情况下,后随车与前车发生追尾碰撞的风险.

1.2 追尾碰撞运动过程分析

由于车辆制动减速过程相对较为复杂,其制动减速度增长阶段时间较其他制动过程相应的时间短,因此,以往研究者通过将车辆制动过程中制动减速度增长阶段简化的处理方法来计算车辆制动停车距离[7].以此为基础,可得出两车碰撞状态之前处于不同时间段相应的制动距离,具体如下式所示:

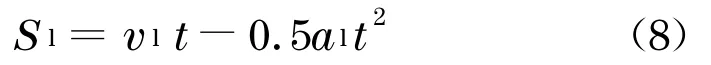
当t≥vl/al时,前车已经完全制动停止,其相应的制动停车距离为

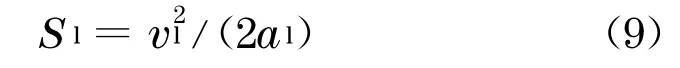
根据制动迟滞时间与停车制动时间的关系,后随车的制动距离可分为

式中:tr为驾驶员反应时间;tb为制动协调时间;tr+tb为制动迟滞时间.

综上所述,根据文献对不同时间段的追尾碰撞研究[8] ,可以得出以下4 种碰撞情形,具体如下:①后车在其制动迟滞时间内与尚未制动停下来的前车发生追尾碰撞;②后车在其制动迟滞时间内与已制动停下来的前车发生追尾碰撞;③后车在其制动持续阶段内与尚未制动停下来的前车发生追尾碰撞;④后车在其制动持续阶段内与已制动停下来的前车发生追尾碰撞.

1.3 追尾碰撞过程能量损失

根据前述, 利用物理运动学定律,计算出处于不同碰撞情形下的追尾碰撞速度.然后运用动量定理,得出两车发生碰撞时的能量损失.

情形①的能量损失:首先,求出其碰撞所需要的时间tc.

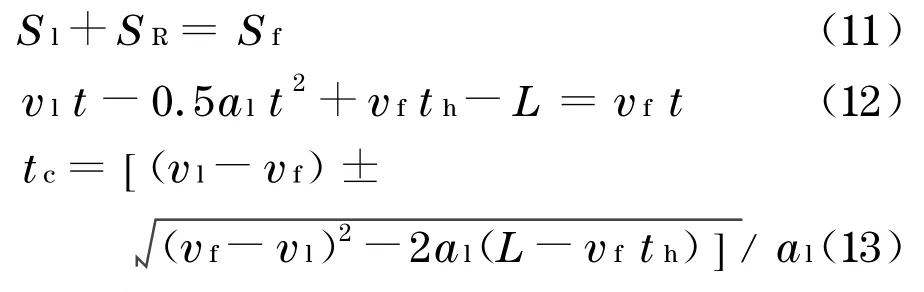
式中:t为车辆行驶时间;th为车头时距;L为前车的车长;

其次计算出发生追尾碰撞时的前车速度vpre_l

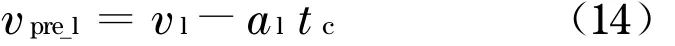
后随车的速度vpre_f由于处在驾驶员反应时间内, 所以其发生追尾时速度保持不变.

然后,根据追尾碰撞的特性, 即碰撞是塑性而且碰撞后两车往往连为一体运动, 运用动量定理计算出追尾碰撞后的两车速度v[9]c.

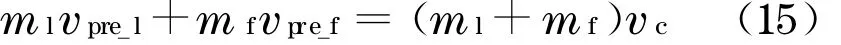
最后,利用能量守恒定律算出两车的能量损失ΔE.

其中,e为恢复系数,e=0 .

同理可得情形②～④的发生碰撞时的速度以及能量损失,限于篇幅,只列举碰撞所需时间.

对于追尾碰撞情形②

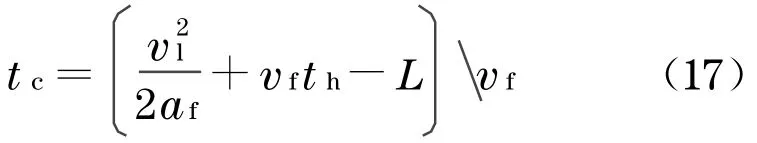
对于追尾碰撞情形③

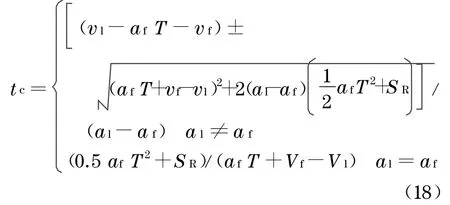
对于追尾碰撞情形④

2 追尾风险计算

2 .1 追尾风险量化方法

根据事故风险的含义, 本文将追尾事故风险定义为在某一时刻特定的道路交通条件下后随车行驶过程中与引导车发生事故的可能性与发生事故的可能严重程度, 所以可以用上述分析得出的追尾概率和能量损失来表征追尾事故风险.

最终, 通过蒙特卡罗法产生随机数的方法来计算高速公路两车追尾时的风险.

2 .2 模型参数标定

根据Lerner对驾驶人的反应时间研究成果[10],取最不利的情况,当前方车辆的紧急制动出乎驾驶员意料时,其反应时间tr 将增加,其服从对数正态分布LN(0.17,0.44),单位为s.制动系统协调的时间tr=0.175s[7] .参照文献[11] 和Aimsun 仿真软件车辆性能模块标定经验的研究成果,考虑不同车辆类型的紧急制动性能差异, 将前引导车客车、货车紧急制动服从正态分布分别定为和,其中为紧急制动最大减速度,ae, min为紧急制动最小减速度.由于考虑的是追尾危险情况,笔者认为后随车将采取最大制动减速度去应对这种最严峻的情形从而将追尾风险减少至最低.因此,根据追尾机理分析得出的结论可以认为,所计算得到的追尾风险概率是在前车紧急制动情况下、后随车虽采取最大制动减速的措施下仍无法避免两车追尾碰撞的可能性.

2 .3 追尾风险影响因素分析

以高速公路上前后两辆行驶的小客车为例, 其车质量都为2 500 kg,车长都为4 .5 m .则根据上述计算方法和参数假设,得出在前车车速为30 m ·s-1时, 跟随车辆在不同车速及车头时距情况下两车追尾概率及能量损失构成的追尾实时风险如图1 .

从图中可以看出,当两车车头时距一定, 追尾概率和能量损失随着车速增加而急剧增大;当两车车速一定, 追尾概率随着车头时距的增加而急剧减少,

能量损失直至车头时距大于2 s 时才出现急剧减少趋势.即使两车行驶速度相同, 车头时距为1 .5 s时,追尾概率也很大, 为12 .2 %.同时,随着车头时距的增大, 发生第①种追尾情形的比重大幅降低,第④种追尾情形的比重却急剧增加.为了更加说明车头时距、后车跟驰速度对追尾风险概率的影响程度, 本文对此进行敏感性分析.测定敏感程度的指标就是敏感系数,其定义为[12]

式中:Se为敏感系数;target为目标变动百分比;effect为因素变动百分比.

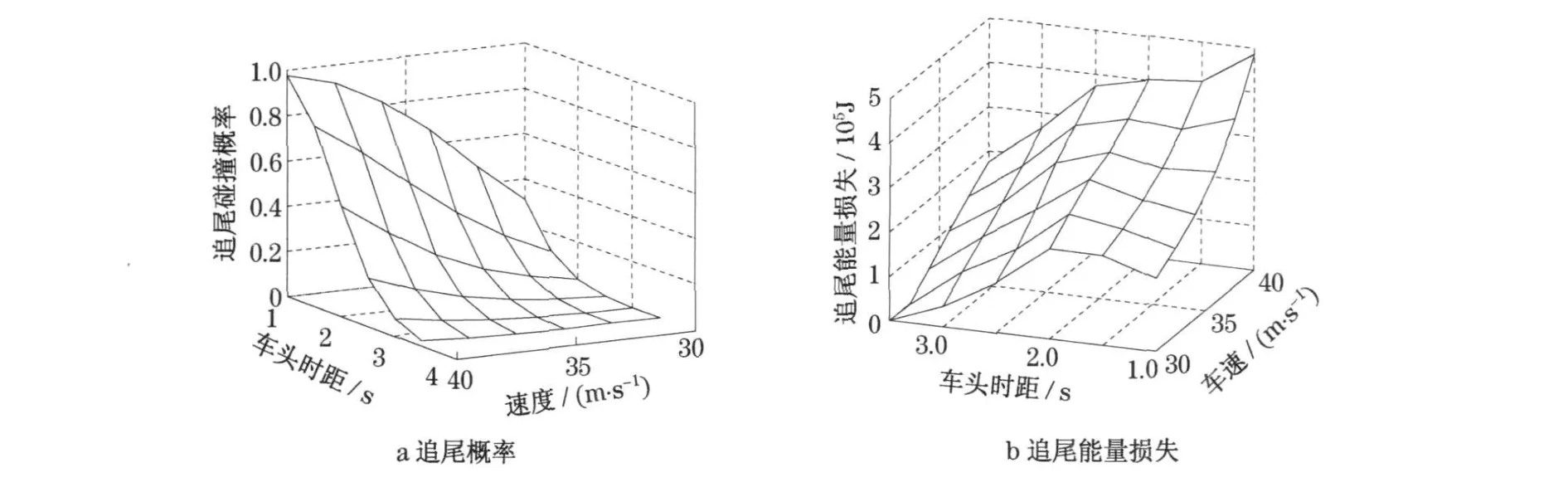
图1 跟驰客车的追尾风险指标Fig 1 Risk indicator of rear-end collision for following car

在上述假设前提下, 通过计算得出当跟驰车速为30 m ·s-1不变时,车头时距从1 .0 s 开始每增加0 .5 s 就计算一次相应的敏感性系数,直至车头时距达到3 .5 s ;当跟驰车头时距为2 .0 s 不变时,其速度从30 m ·s-1开始每增加2 m ·s-1就计算一次相对应的敏感性系数,直至速度达到40 m ·s-1,具体如图2 所示.

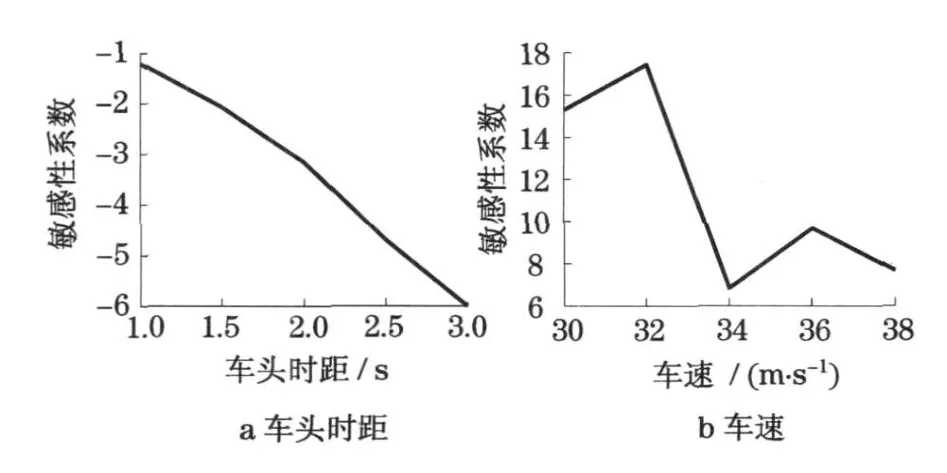
图2 敏感性分析Fig 2 Sensitivity analysis

从图中可以发现车头时距、后车跟驰车速对追尾概率有着重要影响.随着车头时距不断增大, 其敏感系数几乎在不断减少, 其中当车头时距增至到3 s时,敏感系数达到-6 .这说明了车头时距增加将降低追尾风险概率,其降低幅度较大, 可以达到车头时距增加1 %而追尾风险概率将减少6 %的程度.同时,随着车速增加, 其敏感系数急剧波动, 没有呈现与速度相应的一致性变化.但敏感系数值都相对较大,甚至能因后车车速增加1 %导致追尾风险概率能达到17 %左右的情形发生.这更加充分说明限速的重要性.

2 .4 跟驰追尾风险评价

由于用于衡量追尾风险的能量损失在计算过程中考虑了不同类型车辆的质量, 给实际运用带来困难,因此,用相对简单的两车追尾碰撞时的绝对速度差来表示追尾风险所蕴含的事故严重程度,其形式如下:

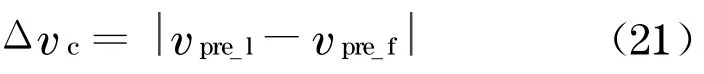
式中:Δvc表示碰撞前两车速度差.

通过上述2 个衡量追尾风险的指标来综合表征高速公路跟驰追尾风险.

2 .5 等级阈值确定

本文先用标定过的Aimsun 仿真软件来获取车辆数据信息;然后结合追尾事故率和严重程度经验常识及模糊C 聚类法处理上述车辆运动状态数据计算结果将追尾概率划分为4 级, 分别表示为:小(0 ,0 .015] ,用1 表示;中等(0 .015,0 .050],用2 表示;稍大(0 .050,0 .200],用3 表示;大(0 .200,0 .500] ,用4 表示;很大(0 .500,1 .000],用5 表示。将追尾严重程度划分为低(0,3 .5],单位m · s-1,用1 表示;中(3 .5,8 .0],单位m · s-1,用2 表示;高(8 .0,+∞), 单位m ·s-1,用3 表示.根据工程风险评价技术, 建立跟驰追尾风险矩阵图,如图3 .其中矩阵里1 表示低风险区,2 表示中等风险区, 3 表示中高风险区, 4 表示高风险区.

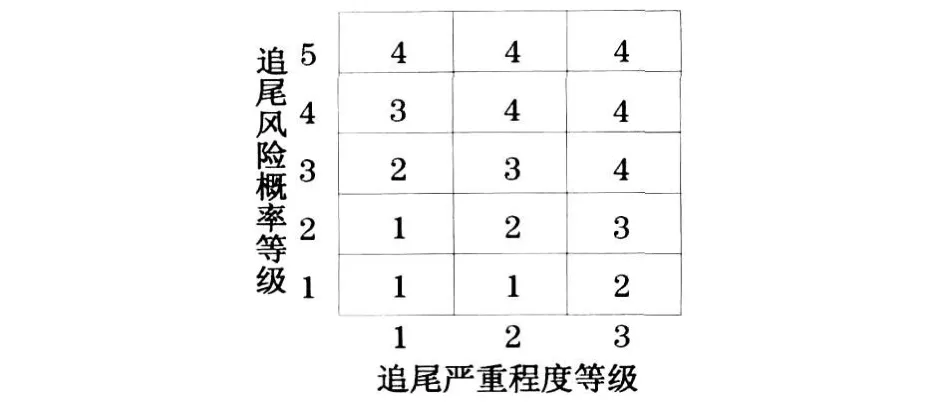
图3 跟驰追尾风险矩阵Fig 3 Risk matrix of rear-end collision

3 结语

根据高速公路行车安全距离公式对追尾事故机理进行了分析, 得出了4 种追尾碰撞情形, 发现当车流中一旦有驾驶员产生需要较长反应时间的情形,就可能导致随后车流中某一车辆不可避免地发生追尾事故.结合动量定理, 得出了追尾碰撞严重程度,构建出了相关的跟驰追尾风险指标.通过基于蒙特卡罗的数值计算方法和敏感性分析, 发现车头时距和后车车速的选择是追尾概率大的最主要影响因素,建议高速公路最小车头安全时距保持在2 .0 s .同时,以追尾碰撞速度差来简化追尾风险指标, 提出了基于模糊聚类的等级阈值划分方法, 最终阈值的合理确定还需在今后通过大量的交通仿真及实际运用来进一步完善,使其更具有应用价值,从而更好地为行车安全和交通流风险状态预警提供理论支撑.

[1] Mohamed Abdel-AT Y.Analy sis of driver injury severity levels at multiple locations using ordered probit models [J] .Journal of Safety Research, 2003, 34:597.

[2] 朱彤, 赵永红, 白玉, 等.跟车风险的概率估计方法研究[J] .计算机工程与应用, 2009, 45(1):13.ZH U Tong,ZH AO Yonghong,BAI Yu,et al.Study of carfollow ing risk estimation by probability method[J] .Computer Engineering and Applications,2009, 45(1):13.

[3] 陆斯文, 方守恩, 王俊骅.单车道行人激进过街冲突和碰撞事故机理分析[J] .重庆交通大学学报:自然科学版, 2009, 28(1):108.LU Siwen, FANG Shouen, WANG Junhua .Mechanism Analysis on conflicts and collisions caused by aggressive pedestrian crossing single lane [J] .Journal of Chongqing Jiaotong University :Natural Science,2009, 28(1):108.

[4] 郑安文.高速公路行车间距分析与防追尾装置开发[J] .武汉理工大学学报, 2002, 24(9):62.ZH ENG Anw en.The analy sis of the motorway vehicle gap and designing the device of protectiving vehicle collision[J] .Journal of Wuhan University of Techonolgy,2002, 24(9):62.

[5] Gary A,Davis, Tait Sw enson.Collective responsibility for freeway rear-ending accidents? an application of probabilistic causal models[J] .Accident Analysis and Prevention, 2006, 38:728.

[6] Kim Joonki, Wang Yinhai.Modeling the probability of freeway rear-end crash occurrence [J] .Journal of Transportation Engineering,2007, 133(1):11.

[7] 徐杰, 杜文, 孙宏.跟随车安全距离的分析[J] .交通运输工程学报, 2002, 2(1):101.XU Jie,DU Wen, SUN H ong .Safety distance about carfollow ing [J] . Journal of Traffic and Transportation Engineering,2002, 2(1):101.

[8] T sao H S, Jacob,Randolph W.H all.A probabilistic model and a softw are tool for avcs longitudinal collision/ safety analysis [R] . Berkeley : Path Program Institute of Transportation Studies of University of California,1993.

[9] 许洪国.道路交通事故分析与处理[M] .北京:人民交通出版社, 2004.XU H ongguo.Road traffic accident analysis and process[M] .Beijing :China C ommunications Press, 2004.

[10] 王殿海.交通流理论[M] .北京:人民交通出版社,2002.WANG Dianhai.Traffic flow theory [M] .Beijing :China Communications Press,2002.

[11] Jason Carbaugh, Datta N Godbole, Raja Sengupta .Safety and capacity analy sis of automated and manual highway sy stems[J] .Transportation Research Part C,1998, 6:69.

[12] 潘晓春.利润敏感性分析——利用函数的弹性求利润的敏感系数[J] .经济师, 2005, 5(9):121.PAN Xiaochun. Profit sensitivity analysis——using the functional elasticity to seek sensitive coefficient for profit[J] .China Economist,2005, 5(9):121.