Banach空间中有限族“三解合一”的混合临近点法*
2011-12-17卢家花王元恒
卢家花, 王元恒
(浙江师范大学数理与信息工程学院,浙江金华 321004)
假定 E是一个实 Banach空间,E*是 E的对偶空间,J:E→2E*是由下式定义的正规对偶映象:
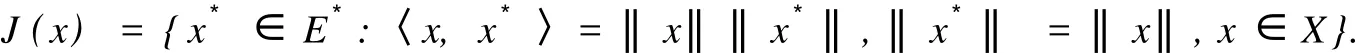
设 C是 E的一个非空闭凸子集,f:C×C→R,其中 R为实数集.均衡问题就是求 p∈C,使得对∀y∈C有下列不等式成立:

把式 (1)的解集记为 EP(f).若映射 T:C→E*,并设 f(x,y)=〈Tx,y-x〉,∀x,y∈Ω,则 x∈EP(f)当且仅当对∀y∈Ω,〈Tx,y-x〉≥0.大量物理和经济学的问题往往可归结为求均衡点,即求式 (1)的解.
设 E是一个光滑严格凸自反的 Banach空间,C是 E的一个非空闭凸子集,可以定义函数 φ为
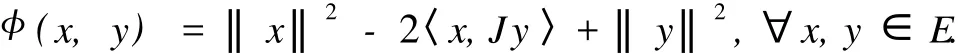
由文献[1]知,对任意的 x∈E作广义投影ΠC:E→C等价于求 φ(x,y)的最小值.若 ΠCx=x,则

当 E为 Hilbert空间时,φ(x,y)=‖x-y‖2.
把映射 T:C→C的不动点集记为 F(T).若对∀x∈C和 p∈F(T)有 φ(p,Tx)≤φ(p,x),则称 T为半点,把 T的渐近不动点集记为 F^(T);若 F^(T)=F(T),则称 T为相对非扩张的.易知半相对非扩张是相对非扩张的推广.

若 E是一致光滑的,则 J在每一有界集上是一致范-范连续的.
2009年,文献[3]在一致凸和一致光滑的 Banach空间 E中证明了由

所生成的 2个迭代序列{xn}和{un}在一定条件下强收敛于 z=ΠF(x0).其中:ΠF:E→F为广义投影;F:=F(T)∩F(S)∩EP(f).
2009年,文献[4]又引进并证明了由

所产生的迭代序列{xn}在一定条件下强收敛于ΠT-1(0)∩EP(f)(x0).
受以上文献的启发,本文在一致凸和一致光滑的 Banach空间 E中,利用文献 [4]的方法,在文献[3]的基础上,引入新的关于有限个半相对非扩张映射的混合迭代序列证明了当 {δn},{αn},{βn},{γn},{rn}满足一定条件时,式 (2)中的序列 {xn}强收敛于ΠF(x0).其中:

引理 1[5]在一致凸和光滑的 Banach空间 E中,{xn},{yn}是 E的 2个序列,如果 φ(xn,yn)→0且序列{xn},{yn}中有一个有界,那么‖xn-yn‖→0.
引理 2[1]设 E是光滑、严格凸、自反的 Banach空间,C是 E的非空闭凸子集,x∈E,z∈C,则 z=ΠCx当且仅当〈y-z,Jx-Jz〉≤0,∀y∈C.
引理 3[1]设 E是自反、严格凸和光滑的 Banach空间,C是 E的非空闭凸子集,y∈E,则φ (x,ΠCy)+φ (ΠCy,y)≤φ(x,y),∀ x∈C.
引理 4[6]设 E是一致凸的 Banach空间,Br(0)是 X的闭球,则存在一严格增凸泛函 g:[0,∞)→[0,∞)且 g(0)=0,使得 ‖λx+μy+γz‖2≤λ‖x‖2+μ‖y‖2+γ‖z‖2-λ μg(‖x-y‖).其中:∀ x,y,z∈Br(0);λ,μ,γ∈[0,1],λ +μ+γ=1.
引理 5[5]设 E是光滑和一致凸的 Banach空间,r>0,则对∀x,y∈Br,都存在一严格增、连续的凸泛函 g:[0,2r]→R,使得 g(0)=0且 g(‖x-y‖)≤φ(x,y).
为解决 f:C×C→R的平衡问题,先假设 f满足以下条件 (简称 f的条件):
1)f(x,x)=0,∀ x∈C;
2)f是单调的,即 f(x,y)+f(y,x)≤0,∀x,y∈C;

引理 6[7]设 C是光滑、严格凸、自反的 Banach空间 E的一个非空闭凸子集,r>0,x∈E.如果 f:C×C→R是满足 f的条件 1)—条件 4)的双函数,那么存在 z∈C,使得

引理 7[8]设 C是一致光滑、严格凸、自反的 Banach空间 E的一个非空闭凸子集,f:C×C→R满足 f的条件 1)—条件 4),r>0,x∈E,定义一映射 Tr:E→C为
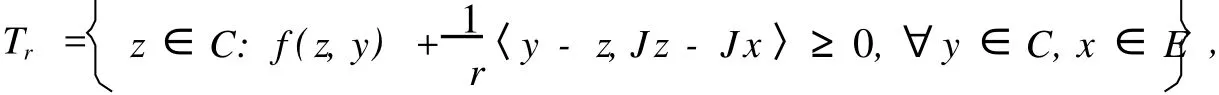
则有以下结论成立:
1)Tr是单值的;
2)Tr是固定非扩张的等价于〈Trx-Try,JTrx-JTry〉≤〈Trx-Try,Jx-Jy〉,∀ x,y∈E;
3)F(Tr)=EP(f);
4)EP(f)是闭凸集.
引理 8[9]设 C是光滑、严格凸、自反的 Banach空间 E的一个非空闭凸子集,f:C×C→R满足 f的条件 1)—条件 4),r>0,则对 x∈E及 q∈F(Tr),有
选择2015年12月—2017年12月接受治疗的100例急性胆源性胰腺炎患者为对象,随机分为两组,每组各50例,对照组男28例,女22例,年龄20~73岁,平均年龄为(42.21±10.67)岁;观察组男26例,女24例,年龄21~74岁,平均年龄为(42.32±10.56)岁。两组患者均进行检查确诊为对急性胆源性胰腺炎,患者在了解实验基本信息后,签署研究同意书。对两组患者各指标进行比较,差异无统计学意义(P>0.05)。

定理 1 设 E是一致凸和一致光滑的 Banach空间,C是 E的非空闭凸子集,双函数 f:C×C→R满足 f的条件 1)—条件 4),令{T1,T2,…,TN},{S1,S2,…,SN}是 C上的两族闭半相对非扩张映射族,假设{βn},{γn}是 [0,1]中的序列 ,满足下列条件 :
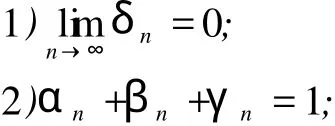

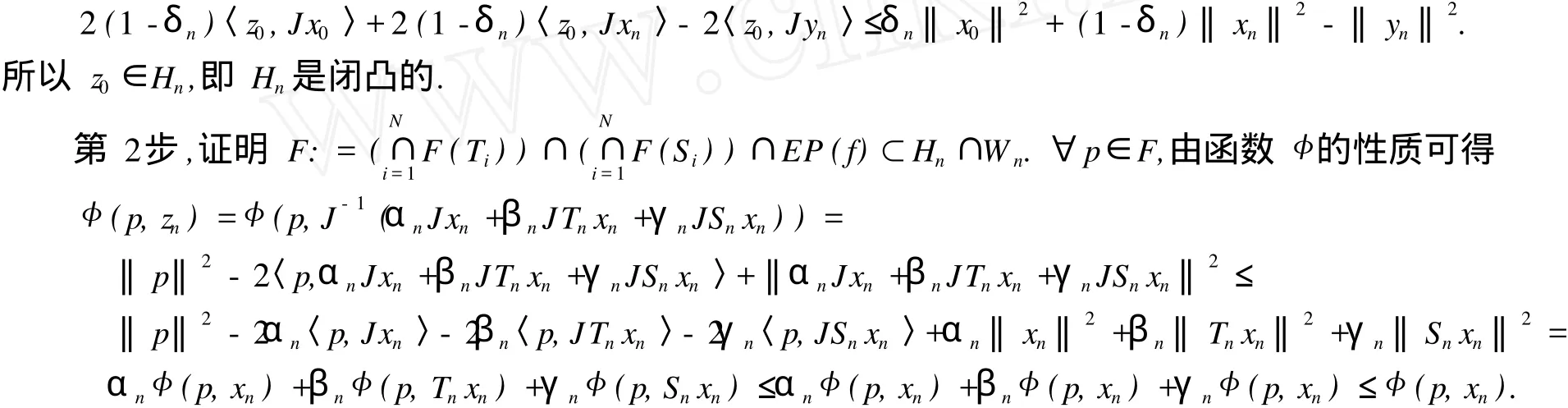
同理可得

令 un=Trnyn,可得

由 Hn的定义知 p∈Hn,即 F⊂Hn.
下证 p∈F⊂Wn.用归纳法,当 n=0时,F⊂C⊂W0.假设 F⊂Wn,下证 F⊂Wn+1.因为 xn+1=
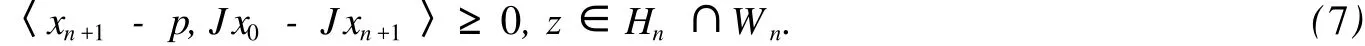
由 Wn的定义知,p∈Wn+1,所以 p∈Hn∩Wn,即 F⊂Hn∩Wn,则 xn是有定义的.

式 (4)+式 (5)可得
所以 φ(xn,x0)是有界的,由上可知 φ(xn,x0)是收敛的.因为
所以{xn}是有界的.再由引理 3得

由Wn的构造知,对任意的正整数 m,n,若 m≥n,则均有Wm⊂Wn且 xm=ΠWm(x0)∈Wn,因此
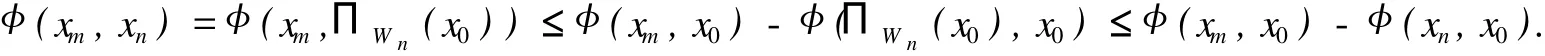
令上式中的 m,n→∞,有 φ(xm,xn)→0.再由引理 1得‖xm-xn‖→0(m,n→∞),从而{xn}是柯西列.又因 E是 Banach空间且Wn是闭凸的,所以{xn}是收敛的.

再由引理 1得:

由式 (12)和引理 4得
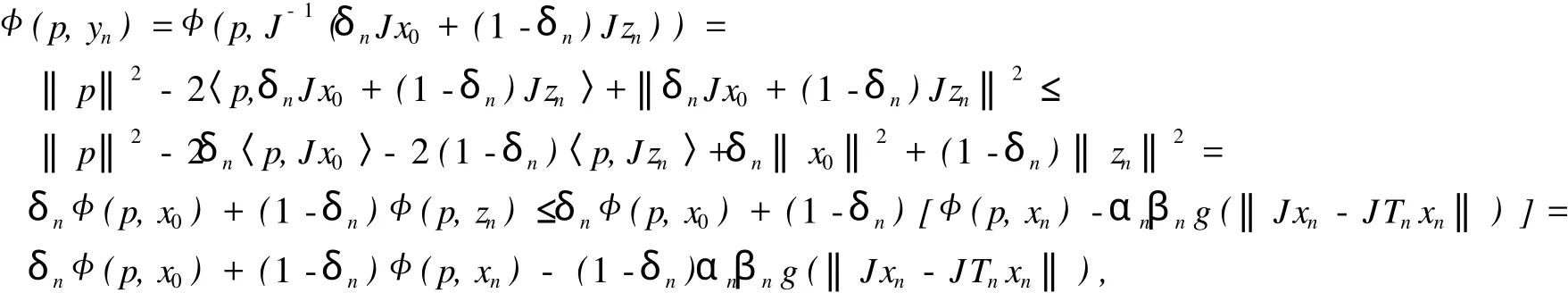
则
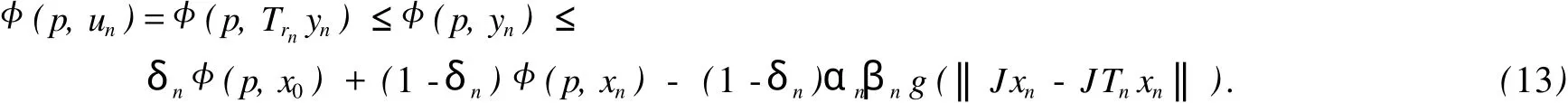
对式 (13)移项并整理得
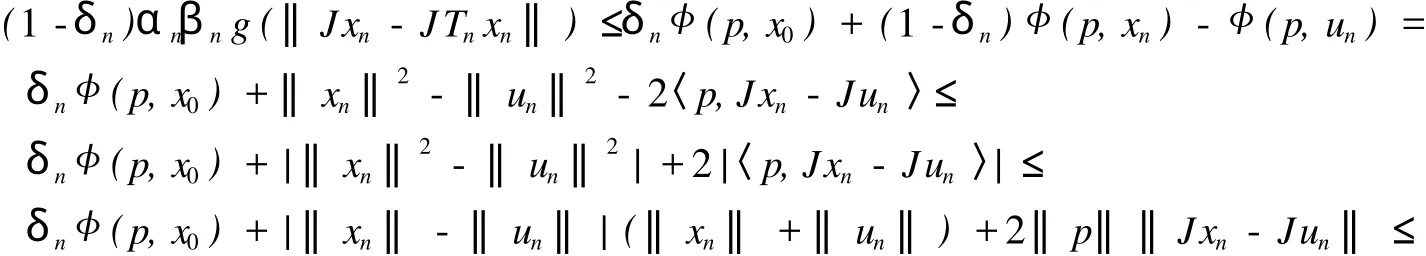

第 5步,证明 x*∈EP(f).由引理 8得

由式 (11)及 xn→x*,可得 un→x*(n→∞).于是当 n→∞时,对式 (14)取极限得 f(y,x*)≤0,∀y∈C.令 yt=ty+(1-t)x*,∀ y∈C,0 最后证明 x*=ΠF(x0).对式 (7)取极限可得〈x*-z,Jx0-Jx*〉≥0,z∈F⊂ Hn∩Wn,由引理 2得x*=ΠF(x0).定理 1证毕. 注 1 当 n=2时,定理 1的结果即为文献[3]的结果,但证明方法不同.因此,本文结果改进和推广了文献[3-4,7-9]等相应的结果. [1]王元恒,曾六川.Banach空间中广义投影变形迭代法的收敛性[J].数学年刊,2009,30A(1):55-62. [2]宣渭峰,王元恒.双复合修正的 Ishikawa迭代逼近非扩张映像不动点[J].浙江师范大学学报:自然科学版,2009,32(4):401-405. [3]Wattanawitoon K,Kumam P.Strong convergence theorems by a new hybrid projection algorithm for fixed point problems and equilibrium problems of two relatively quasi-nonexpansive mappings[J].NonlinearAnalysis:Hybrid Systems,2009,3(1):11-20. [4]CengL C,Mastroeni G,Yao J C.Hybrid proximal-pointmethods for common solutions of equilibrium problems and zeros ofmaximalmonotone operators[J].J Optim TheoryAppl,2009,142(3):431-449. [5]Kamimura S,TakahashiW.Strong convergence of a proximal-type algorithm in a Banach space[J].SI AM J Optim,2002,13(3):938-945. [6]Cho Y J,Zhou Haiyun,Guo Ginti.Weak and strong convergence theorems for three-step iterations with errors for asymptotically nonexpansive mappings[J].ComputMath Appl,2004,47(4/5):707-717. [7]Blum E,OettliW.From optimization and variational inequalities to equilibrium problems[J].Math Student,1994,63(4):123-145. [8]TakahashiW,Zembayashi K.Strong and weak convergence theorems for equilibrium problems and relatively nonexpansive mappings in Banach spaces[J].NonlinearAnalysis:Theory,Methods&Applications,2009,70(1):45-57. [9]TakahashiW,Zembayashi K.Strong convergence theorem by a new hybrid method for equilibrium problems and relatively nonexpansive mappings[J].Fixed Point TheoryAppl,2008,2008:528476.
