(2+1)-维色散长波方程新的精确行波解*
2011-12-17戴振祥徐园芬
戴振祥, 徐园芬
(1.宁波教育学院 信息与艺术学院,浙江 宁波 315010;2.浙江万里学院 基础学院,浙江 宁波315101)
0 引言
(2+1)-维色散长波方程[1]为
方程(1)是描述水波通过等深、狭长理想运动水道的重要方程,其中u(x,y,t),v(x,y,t)为所示变量的物理场.文献[2]给出了式(1)的一组广义对称及其李代数结构;文献[3]利用齐次平衡法得到了式(1)的一些精确孤波解;文献[4]给出了式(1)的类孤子解;文献[5]给出了式(1)的孤子解和有理分式解析解;文献[6]利用广义射影Riccati方程得到了精确行波解;文献[7]利用扩展椭圆函数有理展开解法得到了冲击波解和孤立波解.本文将利用平面动力系统方法[8-11]研究该方程行波解的动力学性质,在给定的参数条件下,求出方程(1)新的峰形(谷形)光滑孤立波解和周期波解.
为研究方程(1)的行波解,作如下行波变换:

把式(2)的第1个方程关于ξ积分2次,第2个方程关于ξ积分1次,并取积分常数为0,得

方程(4)等价于系统

并有以下首次积分:

下面的目标是:首先通过定性分析得到系统(5)随参数改变的相图,然后得到方程(1)在参数平面上不同区域内的行波解的精确参数表达式.
1 系统(5)的所有相图
先求系统(5)的平衡点.

设E(φe,0)为系统(5)的任一平衡点,M(φe,0)是系统(5)的线性化系统在该平衡点处的系数矩阵,用 J(φe,0)表示其 Jacobi行列式,经计算得 J(φe,0)= - f'(φe).由平面动力系统分支理论[8-11]知,作为Hamilton系统(5)的平衡点,当 J>0(或 J<0)时,E(φe,0)是中心(或鞍点);当 J=0并且其Poincaré指标为零时,E(φe,0)是尖点.


通过定性分析知,随着参数c,a的改变,系统(5)有如图1、图2所示的相图.
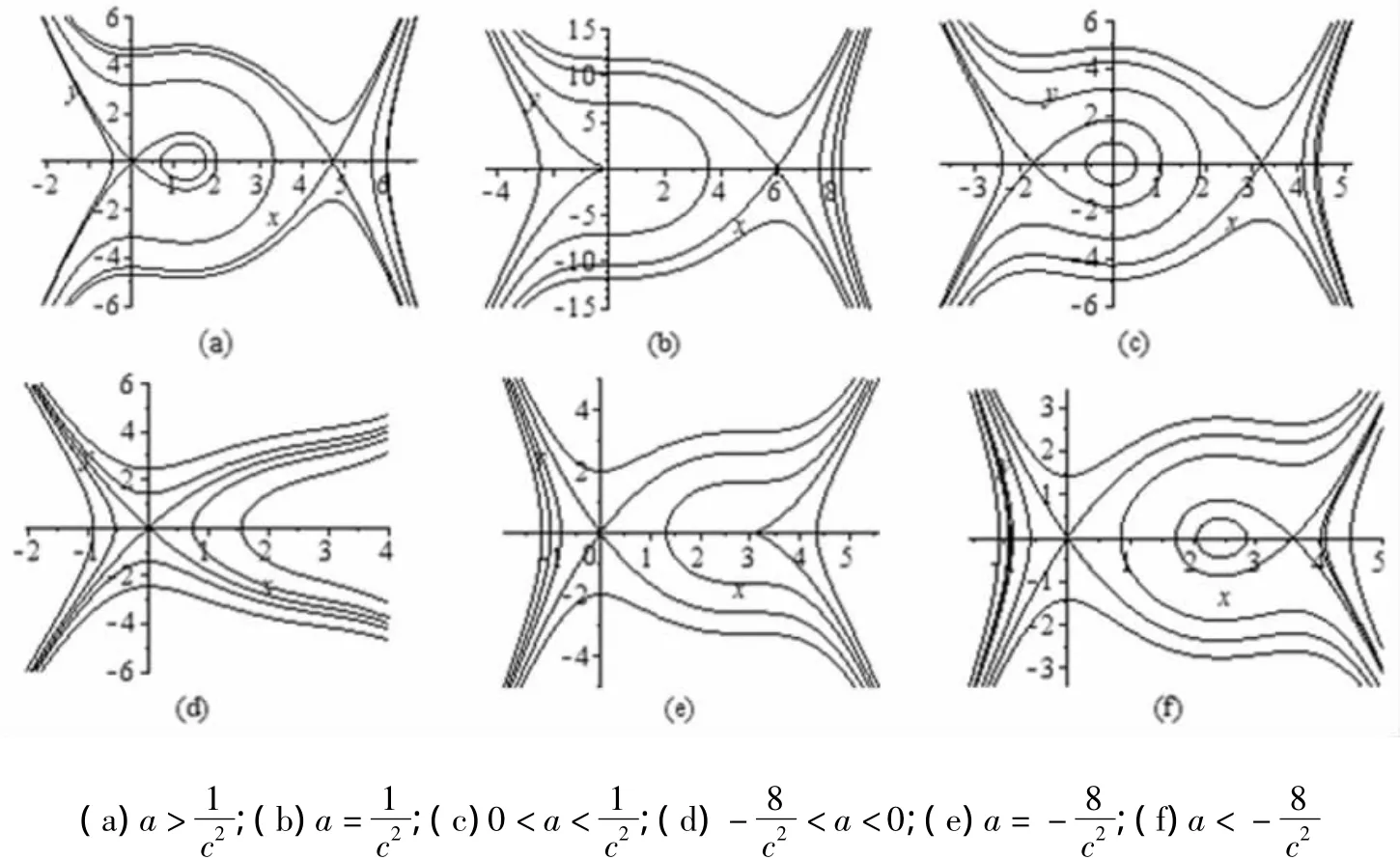
图1 当c>0时系统(5)的相图
图2 当c<0时系统(5)的相图
2 方程(1)孤立波、周期波解的存在性和参数表示
根据以上结果和奇非线性行波方程研究的动力系统方法[8]知,下面的结论成立:
定理1 若下列条件之一成立,则方程(1)存在一峰形或谷形光滑孤立波解:

定理2 若下列条件之一成立,则方程(1)存在一族峰形或谷形光滑周期波解:

下面计算方程(1)在不同的参数条件下其光滑孤立波解和周期波解的参数表达式.

(5)的第1个方程得

经计算得到方程(1)的峰形光滑孤立波解的参数表达式为

②对应于系统(5)并由式(6)定义的水平曲线 H(φ,y)=h(h∈(h2,0)),设参数 r1,r2由

所定义,其中r1>r2>φ>r3>r4.利用系统(5)的第1个方程得

经计算得到方程(1)的峰形光滑周期波解的参数表达式为


所定义,其中0>φ>r3>r4.利用系统(5)的第1个方程得

经计算得到方程(1)的谷形光滑孤立波解的参数表达式为

②对应于系统(5)并由式(6)定义的水平曲线H(φ,y)=h(h∈(h1,0)),经计算得到方程(1)的谷形光滑周期波解的参数表达式同式(8).

所定义,其中r1>r2>φ>φ2.利用系统(5)的第1个方程得

经计算得到方程(1)的峰形光滑孤立波解的参数表达式为

②对应于系统(5)并由式(6)定义的水平曲线H(φ,y)=h(h∈(0,h2)),经计算得到方程(1)的峰形光滑周期波解的参数表达式同式(8).

所定义,其中φ1>φ>r3>r4.利用系统(5)的第1个方程得

经计算得到方程(1)的谷形光滑孤立波解的参数表达式为

②对应于系统(5)并由式(6)定义的水平曲线H(φ,y)=h(h∈(0,h1)),经计算得到方程(1)的谷形光滑周期波解的参数表达式同式(8).

①对应于系统(5)并由式(6)定义的水平曲线H(φ,y)=h1(H(φ,y)=h2),经计算得到方程(1)的谷形(峰形)光滑孤立波解的参数表达式同式(11)(式(10)).
②对应于系统(4)并由式(5)定义的水平曲线H(φ,y)=h(h∈(h2,h1)或h∈(h1,h2)),经计算得到方程(1)的谷形(峰形)光滑周期波解的参数表达式同式(8).
致谢:衷心感谢浙江师范大学赵晓华教授的指导!
[1]洪宝剑,方国昌,卢殿臣,等.(2+1)维色散长波方程新的类孤子解[J].数学的实践与认识,2009,39(1):194-197.
[2]Lou S Y.Symmetries and algebras of the integrable dispersive long wave equations in 2+1 dimensional spaces[J].Phys A,1994,27(2):3235-3243.
[3]Wang Mingliang,Zhou Yubin,Li Zhibin.Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J].Phys Lett A,1996,216(1/2/3/4/5):67-75.
[4]曾昕,张鸿庆.(2+1)维色散长波方程的新的类孤子解[J].物理学报,2005,54(2):504-510.
[5]闫振亚,张鸿庆.2+1维非线性色散长波方程的相似约化和解析解[J].数学物理学报,2001,21A(3):384-390.
[6]智红燕,陈勇,张鸿庆.广义射影Riccati方程方法与(2+1)维色散长波方程新的精确行波解[J].数学物理学报,2005,25A(7):956-964.
[7]向以华,石义霞.(2+1)-维色散长波方程的扩展椭圆函数有理展开解法[J].数学杂志,2009,29(2):206-210.
[8]Li Jibin,Dai Huihui.On the study of singular nonlinear traveling wave equations:Dynamical system approach[M].Beijing:Science Press,2007.
[9]李继彬.(2+1)-维广义 Benney-Luke方程的精确行波解[J].应用数学和力学,2008,29(11):1261-1267.
[10]李继彬.两类Boussinesq方程的行波解分支[J].中国科学:A数学,2008,38(11):1221-1234.
[11]Li Jibin,Liu Zhengrong.Smooth and non-smooth traveling waves in a nonlinear dispersive equation[J].Applied Mathematical Modelling,2000,25(1):41-56.
