遥感影像尺度转换及最优尺度选择探讨

周 觅，张杰林

（核工业北京地质研究院，遥感信息与图像分析技术国家级重点实验室，北京100029）

遥感影像尺度转换及最优尺度选择探讨

周 觅，张杰林

（核工业北京地质研究院，遥感信息与图像分析技术国家级重点实验室，北京100029）

从信息提取的角度阐述遥感影像尺度问题的重要性，评述了尺度效应、尺度转换以及最优尺度选择研究的国内、外现状。重点探讨几种不同尺度转换方法，以及基于像元和面向对象的最优尺度选择方法的技术特点，分析了尺度研究未来发展方向。

尺度效应；尺度转换；最优尺度选择

尺度的概念在不同的应用领域有着不同的诠释。Lam和Quattrochi定义了4种与空间现象有关的尺度［1］：制图尺度，亦称地图比例尺；地理尺度，也称观测尺度，是研究区域的空间扩展，较大范围的研究区域具有较大的地理尺度；运行尺度，指地学现象发生的空间范围，由所研究的地理现象本质决定；测量尺度（也就是分辨率），空间数据集中最小的可分辨单元，越细的分辨单元，其分辨率越高，所具有的尺度也越小。本文着重探讨的是测量尺度。

1 国内、外研究现状

信息提取研究经常用到的一种方法就是影像分类，而分类精度又常常受到测量尺度的影响，国外学者在20世纪80年代就开始了该领域的研究。研究表明，遥感影像的分类精度会受到混合像元数和类别内部光谱变异两个因素的综合影响。当提高影像的空间分辨率时，处于不同类别边缘的混合像元数目减少，分类精度会有所提高；但随着空间分辨率的不断提高，同一类别内部光谱特征的变异性也随之增大，分类精度又有所降低。综上所述，证明了尺度问题研究的重要性。Latty和Hoffer（1981）用最大似然法，选择了同样训练样区对4个不同分辨率的TM影像进行分类，结果证明，随着分辨率的提高，分类精度依次降低，尤其是在相邻像元光谱变异比较大的区域。我国学者也就尺度效应的问题进行了一系列的研究。黄慧萍（2006）利用基于像元的分类技术和基于多尺度分割的面向对象分类技术，对高分辨率影像进行分类实验，分析研究对象尺度与影像分辨率的关系。实验表明，不同地物由于空间尺度不同，与之相适宜的空间分辨率和对象尺度也不同，在适宜的尺度上提取对象信息有更高的精度［2］。

在实际数据处理过程中，针对同一区域不同尺度的地物特征，需要进行尺度转换和尺度叠加来提高信息提取精度。Marceau（1999）认为，多数信息在不同尺度之间的转换必然引起信息的丢失，因此提出了3个需要注意的问题：①如何确定能够正确表达特定地理现象的最佳尺度；②尺度转换的最佳过程、最佳算法；③尺度转换后会产生何种信息损失［3］。除了理论研究外，也有诸多实际应用方面的例子。Goward等（2003）将IKONOS数据（分辨率为全色1 m、多光谱4 m）转换成与Landsat ETM＋分辨率（30 m）相一致的数据，并对两者计算得出的植被指数的差别进行了比较［4］。我国在这方面的研究起步比较晚。李小文（2006）在 “地球表面时空多变要素的定量遥感理论及应用”项目中，综合研究了尺度效应和尺度转换理论、基于先验知识的定量遥感反演理论、同步观测和模拟试验等，取得了一系列研究成果［5］。

目前最佳分辨率选择方法多数是基于统计学理论。例如，Woodcock和Strahler（1987）提出了一种用遥感图像平均局部方差来确定最优尺度的方法，当局部方差达到最大值，则把该分辨率看作是最优尺度［6］。近年来，变异函数的方法也得到了广泛的应用。例如，1997年，Atkinson等通过计算不同分辨率影像的变异函数来确定最优分辨率，变异函数值达到最大时对应的空间分辨率即为最优空间分辨率［7］。此外，还有一些学者对上述方法进行研究；例如，基于可变窗口与可变分辨率改进局部方差方法［8］；一种基于区域生长方法的分割参数选择方案等。

2 尺度转换

尺度转换是指将一幅影像从一个空间或光谱尺度转换到另一个空间或光谱尺度的过程。从小尺度转换到大尺度称为尺度扩展，从大尺度转换到小尺度称为尺度收缩。尺度收缩通常需要通过图像融合的方法实现，本文着重介绍尺度扩展方法研究。

2.1 基于统计的尺度转换方法

基于统计的尺度转换方法是从数据本身出发，只需要考虑遥感数据的空间或是光谱信息，不需要对遥感信息的物理机理有明确的了解。基于统计的方法又可以根据影像分析单元的不同分为基于像元的方法和面向对象的方法。

2.1.1 基于像元的方法

基于像元的方法是比较简便的一种尺度转换方法。它是将图像以n×n窗口为单位合并成为单一、更大窗口的方法。基于像元的方法比较简单、易于实现，常见的算法有局部平均法、中心点法、最近邻法、双线性内插法以及立体卷积法等。本文利用Quick Bird影像（图1a）及其分类图（图1d）进行了不同转换方法的尝试。

（1）局部平均法是将高分辨率遥感影像中n×n窗口内的所有像元的平均像元值作为转换后对应的低分辨率遥感影像的像元值，该方法运算简单，且图像能够很好保持图像均值信息，但却丢失了部分细节信息。

（2）中心点法是将高分辨率遥感影像n×n窗口内中心像元的像元值作为转换后对应低分辨率遥感影像像元值的方法，该方法运算量小，且在一定程度上能保持原影像的纹理，但是随着扩展窗口逐渐变大，转换后的影像会出现不连续的现象。

（3）最近邻法是取高分辨率遥感影像n×n窗口内对应转换后低分辨率遥感影像所映射到位置最近的像元值，见图1b、1e。该方法运算简单，但是与中心点法类似，由于没有考虑其他相邻像元点的影响，转换后的影像会使图像质量有一定损失，出现像元不连续的现象。

（4）双线性内插法是利用高分辨率遥感影像某像元相邻的4个像元值，先对两水平方向进行一阶线性插值，然后再在垂直方向上进行一阶线性插值，得到对应的低分辨率遥感影像的像元值，见图1e。该方法运算量稍大，但是能够克服转换后影像不连续的现象，只是边缘信息仍会有一定损失，转换精度不高。

（5）立体卷积法是一种比较复杂的尺度转换方法，原理同双线性内插的原理。利用高分辨率遥感影像中4×4窗口内16个像元进行加权平均，通过3次插值来计算对应的低分辨率遥感影像的像元值，见图1c、1f。该方法的运算比较复杂，不仅考虑了相邻像元的像元值，还考虑了相邻像元间的灰度值的变化率，因此，能够较好地保留影像的纹理和边缘信息，转换精度也比前几种方法更高。

由图1可见：经过尺度转换后的遥感影像能够最大限度地保留原始影像的空间分辨率和光谱特征；同时，在分类过程中，能够消除部分噪声影响，减弱类别内部的光谱变异，从而提高了分类和信息提取的精度。

2.1.2 面向对象的方法

面向对象的尺度转换方法实际上是对遥感影像纹理特征的提取及分割方法。纹理分割要求在生成影像对象的过程中能压缩高空间分辨率影像，把高空间分辨率像元的信息保留到大尺度的影像上，在影像信息量损失最小的前提下，把高空间分辨率影像的原始信息最大程度地保留到大尺度的影像上，将原始影像成功分割为多个影像多边形对象［9］。

面向对象的尺度转换方法是一种多尺度分割技术，从任一个像元开始，采用自下而上的区域合并方法形成面积大小（尺度）不等的多边形对象［10］。小的对象可以经过若干步骤合并成大的对象，每一对象大小的调整都必须确保合并后对象的异质性小于给定的阈值。显然，设定了较大的分割尺度，则对应着较多的像元被合并，因而产生较大面积的对象。大尺度对象是由小尺度对象合并产生的，所以相邻尺度下的对象可以构成层次结构，使得不同层次间信息的传递成为可能。

经过这种多尺度分割后，影像的基本单元已不是单个像元，而是由同质像元组成的多边形对象。在计算出每一多边形对象所包含像元的光谱信息和多边形的形状信息、纹理信息、位置信息，以及多边形间的拓扑关系信息等的基础上，就可以充分利用对象所提供的各种信息进行组合，针对不同地物，制定不同层次、不同尺度下的具体分类规则，进行信息提取。由于每一层之间都有对应关系，分类规则也可以进行层间传递。

2.2 基于机理的尺度转换方法

基于机理的尺度转换方法是指构建含有多个变量的转换模型，通过高分辨率遥感影像预测低分辨率遥感图像像元值的方法，更符合遥感系统的成像过程。这种基于机理的尺度转换方法通常都有明确的物理意义，且尺度转换精度高。但是由于研究对象不同，场景和过程非常复杂，有可能造成对研究机理的理解不充分，所构建的模型不完备，进而导致基于该机理模型进行的尺度转换存在一定的误差。

点扩散函数法是从信号处理的角度进行的一种尺度转换方法。它描述了当一个点光源的能量输入到传感器时，在影像平面上的能量分布情况。基于点扩散函数的尺度扩展方法，其实质是模拟一个权重窗口，并利用这个窗口对影像进行滤波，然后进行重采样，得到低分辨率影像的过程。权重与窗口中像元的位置有关，位于窗口中心的像元权重值最大，从窗口中心向外，权重值依次减小。

综上所述，基于统计的尺度转换方法从数据本身出发，根据统计信息，针对遥感影像的空间或是光谱数据进行运算，原理比较简单，易于实现。基于机理的尺度转换方法从遥感信息的物理机理出发，根据遥感系统成像过程以及地学过程的各类参数，建立尺度转换模型。因此，基于机理的方法对物理模型的要求非常严格，目前实现起来比较困难。

3 最优尺度选择

由于尺度效应的影响，在多源遥感数据处理与信息提取研究中，需要针对不同应用目的、不同地物尺度，选择最合适的分辨率，最大限度地反映目标地物的空间分布特征，也就是最优尺度选择。本文从基于像元和面向对象两方面来探讨最优尺度选择方法。

3.1 基于像元的最优尺度选择方法

基于像元的最优尺度选择方法需要满足两个条件：一是能够最大限度地反映目标地物的空间分布特征；二是在满足第1个条件的前提下，选择最小的影像分辨率。如果在同一研究区域的遥感影像中有多个感兴趣地物类别，那么就需要选择能够识别面积最小的类别对应的最优尺度。其中，局部方差法是最常见、最简单的方法。

局部方差法是Woodcock和Strahler于1987年提出的一种用于最优尺度选择方法［6］。该方法首先计算了不同空间分辨率影像的平均局部方差，然后研究了平均局部方差随空间分辨率的变化规律，当局部方差达到最大时，则认为该分辨率是影像的最优尺度 （图2）。窗口大小为（2m＋1）（2n＋1）的局部方差法的公式如下：

式中：Xij为i行j列的像元值；μij为以第i行第 j列像元为中心、 以（2m＋1）（2n＋1）为大小的窗口内像元的均值；m，n的取值为自然数，控制滑动窗口的大小。

3.2 面向对象的最优尺度选择方法

面向对象的最优尺度选择的实质其实就是进行区域选择，选择原则是使区域内的同质性以及区域间的异质性最大。具体实现过程可归纳为两个步骤。首先是计算出不同地物类别多边形的面积，通过比较，确定面积最小的一类地物的最大分辨率。然后，进行最优尺度选择。最常用的面向对象的最优尺度选择方法是以对象的方差作为指标的。

与基于像元的最优尺度选择方法不同，面向对象的方差法没有固定大小的滑动窗口，而是把尺度分割后的窗口作为一个计算单元，通过计算每一个单元的方差，选择不同类别地物的最优尺度。计算过程可分为3步：第1步，在面向对象尺度转换方法的基础上，得到不同大小的多个对象窗口；第2步，计算每个对象窗口的均值和整幅影像的均值；第3步，计算每个对象窗口的方差，绘制均值方差与尺度关系曲线。曲线上会出现多个峰值，每个峰值所对应的影像分割尺度就是不同类别地物所对应的最优尺度（图3）。

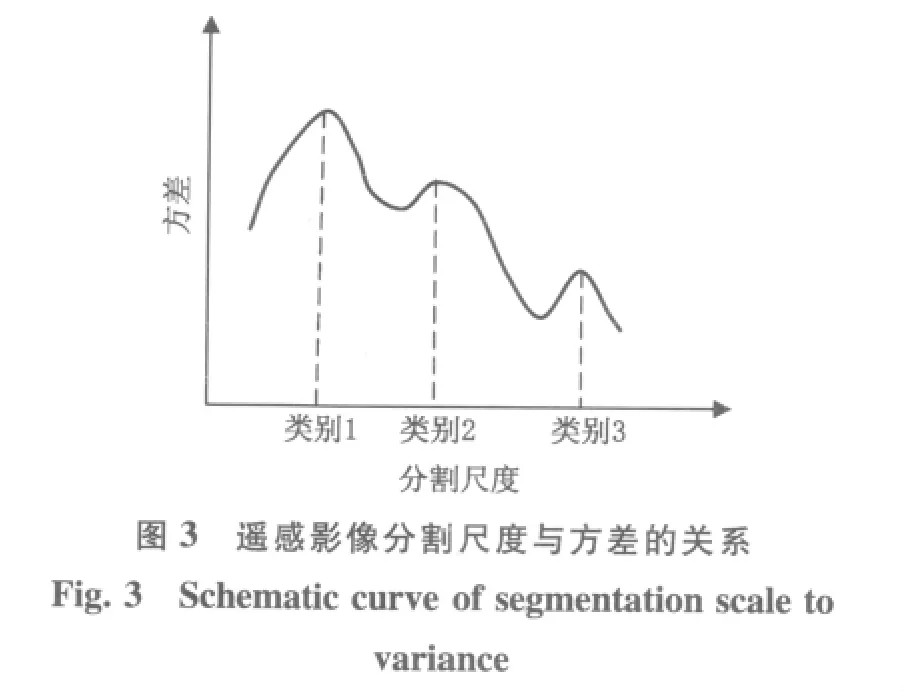
综上所述，基于像元的最优尺度选择方法通常适用于具有相似尺度的地物识别，影像中最好只包含一种尺度下的地物类别。而面向对象的最优尺度选择则可以应用于同一幅影像包含多种尺度地物的情况，该方法能够根据光谱、形状异质性同时确定不同类别地物特有的最优尺度，进而提高信息识别的效率和精度。

4 结论与展望

本文在国内、外资料调研分析的基础上，总结了几种常见的尺度转换和最优尺度选择方法，得到如下两点认识：

（1）基于统计的尺度转换方法从数据本身出发，原理简单，易于实现，但是精度不高；基于机理的尺度转换方法从遥感数据获取及地学过程等物理机理出发，精度比较高，但是对建模要求很高，实现起来难度较大。

（2）基于像元的最优尺度选择方法多适用于相似尺度的地物识别，原理、过程简单；面向对象的最优尺度选择多应用于同一幅影像包含多种尺度地物的情况，信息识别精度高，但是实现过程复杂。

总之，不同尺度转换和最佳尺度方法都有各自的优缺点，如何充分发挥各种方法的优点，要根据研究对象的特点和图像特征进行具体的分析。因此，总结出不同图像特征的评价参数和选择相应的方法，以便更加高效地利用不同尺度遥感数据进行信息提取是今后研究的重点。

［1］Lam N， Quattrochi D A.On the issues of scale，resolution， and fractral analysis in the mapping sciences［J］.Prof.Geogr.， 1992， 44（1）:88-98.

［2］黄慧萍，吴炳方.地物大小、对象尺度、影像分辨率的关系分析［J］.遥感技术与应用，2006，21（3）:243-248.

［3］Marceau D J， Hay G J.Remote sensing contributions to the scale issue［J］.Canadian Journal of Remote Sensing， 1999， 25（4）:357-366.

［4］Goward S N， Davis P E， Fleming D， et al.Empirical comparison of Landsat 7 and IKONOS multispectral measurements for selected Earth Observation System（EOS） validation sites［J］.Remote Sensing of Environment， 2003， 88（1-2）:80-99.

［5］李小文.地球表面时空多变要素的定量遥感项目综述［J］. 地球科学进展， 2006， 21（8）:5-14.

［6］Woodcock C E，Strahler A H， The factor of scale in remote sensing ［J］. Remote Sensing of Environment， 1987， 21（3）:311-332.

［7］Atkinso P M，Kelly R E J.Scaling-up point snow depth in the U.K.for comparison with SSM/I imagery［J］.InternationalJournalofRemote Sensing，1994， 18（2）:437-443.

［8］明冬萍，王 群，杨建宇.遥感影像空间尺度特性与最佳空间分辨率选择［J］.遥感学报，2008，12（4）:529-537.

［9］黄慧萍.面对对象影像分析中的尺度问题研究［D］.北京，中国科学院遥感应用研究所，2003.

［10］陈云浩，冯 通，史培军，等.基于面向对象和规则的遥感影像分类研究［J］.武汉大学学报：信息科学版， 2006， 31（4）:316-320.

Review on scale transformation for remote sensing image and selection of optimal spatial resolution

ZHOU Mi，ZHANG Jie-lin
（National Key Laboratory of Remote Sensing Information and Image Analysis Technology，Beijing Research Institute of Uranium Geology， Beijing 100029， China）

The importance of scale issues is described in this paper.It also reviews the situation of the study on scale effect， scale transformation and selection of optimal scale.Then， several scale transformation algorithms have been discussed，and the technical characteristics of selected methods of optimal scale based on pixel and object are studied.In the end，the future directions of the scale issues are analyzed.

scale effect； scale transformation； selection of optimal scale

TP751；TP79

A

1672-0636（2011）02-0094-05

10.3969/j.issn.1672-0636.2011.02.006

2010-10-27；

2011-03-25

周 觅（1986—），女，内蒙古包头市人，在读硕士研究生，研究方向：高光谱遥感及地学应用。E-mail:xiaomio116@sina.com